ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра «Высшая математика»

СБОРНИК

типовых расчётов

по теории вероятностей

Часть 1

«Случайные события»

Ижевск 2010

УДК 519.21 (075.8)

Рассмотрено и одобрено на заседании кафедры «Высшая математика» (протокол от 23.11.2009г. № 70)

Рецензент: Ицков А.Г, кандидат физико-математических наук, доцент кафедры «Прикладная математика и информатика»

Данелян А.В., Корякина Н.Р., Пушина Е.Г.

Сборник типовых расчетов по теории вероятностей для студентов технических специальностей ИжГТУ. Ч. 1 Случайные события. – Ижевск: Изд-во ИжГТУ, 2010. – 44 с.

Методическое пособие предназначено для проверки текущих знаний. Может быть использовано также для самостоятельной работы студентов и подготовки к экзамену. Приведены примеры решения некоторых задач по теории вероятностей. Предназначено для студентов технических специальностей ИжГТУ.

© Данелян А.В., Корякина Н.Р.,

Пушина Е.Г.

© Издательство ИжГТУ, 2010

СОДЕРЖАНИЕ

Основные понятия теории вероятностей …………………………..4

Примеры решения задач типового расчета……………………….10

Типовые расчеты……………………………………………………21

Литература…………………………………………………………..41

Приложение 1……………………………………………………….42

Приложение 2……………………………………………………….43

Основные понятия теории вероятностей

Виды случайных событий

Случайным называется событие, которое при данных условиях может либо произойти, либо не произойти.

Например, событие “при бросании монеты выпал герб” – случайное.

Достоверным называют событие, которое обязательно произойдет в результате опыта.

Невозможным называется событие, которое заведомо не произойдет в условиях опыта.

Достаточно большое число однородных (т.е. происходящих при одних и тех же условиях) случайных событий подчиняется определенным, так называемым вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.

События называются несовместными, если появление одного из них исключает появление других в одном и том же испытании. В противном случае события совместны.

Несовместные события А₁, А₂…А_n образуют полную группу, если в результате опыта обязательно происходит хотя бы одно из них.

Классическое определение вероятности

Вероятность является одним из основных понятий теории вероятностей.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов (m) к общему числу исходов (n).

Таким образом, вероятность события А определеяется по формуле

Суммой событий А и В называют событие А+В, состоящее либо в появлении А, либо в появлении В, либо в их совместном появлении.

Произведением событий А и В называют событие АВ, состоящее в совместном появлении этих событий.

Теорема сложения вероятностей несовместных событий

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Теорема сложения вероятностей совместных событий

Вероятность появления хотя бы одного из двух совместных событий (т.е. вероятность их суммы) равна сумме вероятностей каждого в отдельности без вероятности их совместного появления:

Теорема о вероятности полной группы событий

Сумма вероятностей событий , образующих полную группу, равна единице:

Таким образом сумма событий А₁, А₂…А_n есть событие достоверное.

Противоположными называют два единственно возможных события , образующих полную группу.

Например, попадание и промах при одном выстреле – противоположные события.

Теорема о вероятностях противоположных событий

Сумма вероятностей противоположных событий равна единице:

.

Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого.

В противном случае события называют зависимыми.

Теорема умножения вероятностей независимых событий

Вероятность совместного появления двух независимых событий (т.е. вероятность произведения этих событий) равна произведению вероятностей этих событий:

Теорема о вероятности появления хотя бы одного события

Вероятность появления хотя бы одного из событий , независимых в совокупности, равна разности между единицей и произведениями вероятностей противоположных событий :

,

где А – появление хотя бы 1 из событий ,

- вероятности событий .

Условной вероятностью называют вероятность события В, вычисленную в предположении, что событие А уже произошло.

Теорема умножения вероятностей зависимых событий

Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Формула полной вероятности, формула Байеса

Пусть событие А может наступить лишь при условии появления одного из несовместных событий которые образуют полную группу. Эти события называют ещё гипотезами. Известны вероятности гипотез и соответствующие условные вероятности события А .

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий образующих полную

группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

.

Эта формула называется формулой полной вероятности.

Если событие А уже произошло, для нахождения так называемой переоценённой вероятности гипотез применяется формула Байеса:

Повторные независимые испытания, формула Бернулли

Если производится несколько испытаний, причём вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Пусть производится независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Будем считать, что вероятность наступления события А в каждом испытании постоянна и равнаp. Следовательно, вероятность ненаступления события А в каждом испытании равна q=1-p.

Вероятность того, что при независимых испытаниях интересующее нас событие наступит ровнораз определяется по формуле Бернулли

.

Здесь - число сочетаний изэлементов по, определяется по формуле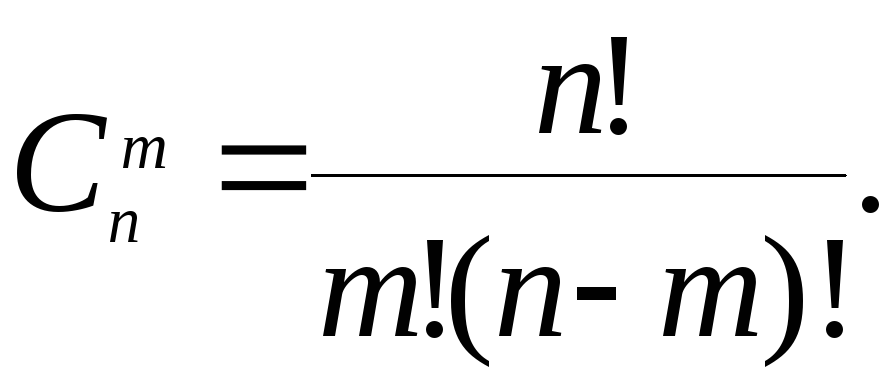

Легко видеть, что пользоваться формулой Бернулли при больших значениях достаточно трудно, так как требуется выполнение действий над громадными числами. Приведённая ниже теорема даёт асимптотическую формулу, которая позволяет приближённо найти вероятность появления события ровнораз прииспытаниях, если число испытаний достаточно велико.

Локальная теорема Лапласа

Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится виспытаниях ровнораз приближённо определяется по формуле

при .

Эта формула называется ещё формулой Муавра-Лапласа.

Значения функции 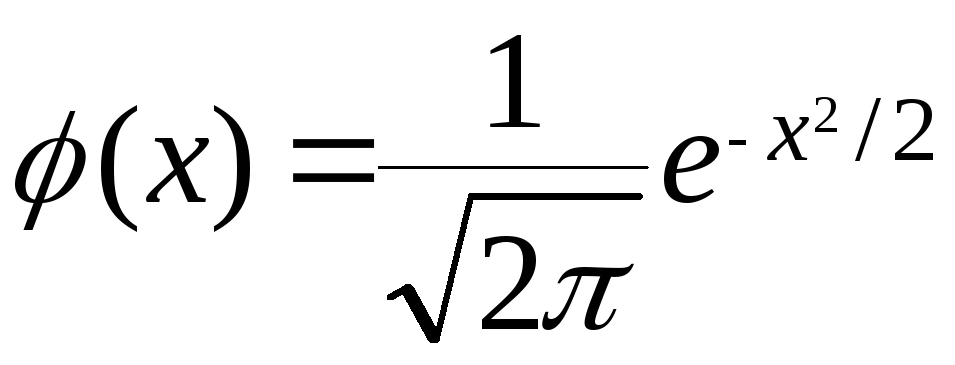находят по таблице (см. приложение 1) для положительных значений аргумента. Для отрицательных значений пользуются той же таблицей, так как функциячётна, т.е..

Для вычисления вероятности того, что интересующее нас событие А появится в испытаниях не менееи не болеераз применяется

Интегральная теорема Лапласа

Если вероятность р наступления события А в каждом испытании постоянна, отлична от нуля и единицы, то вероятность того, что событие А появится в испытаниях отдораз, приближённо равна определённому интегралу

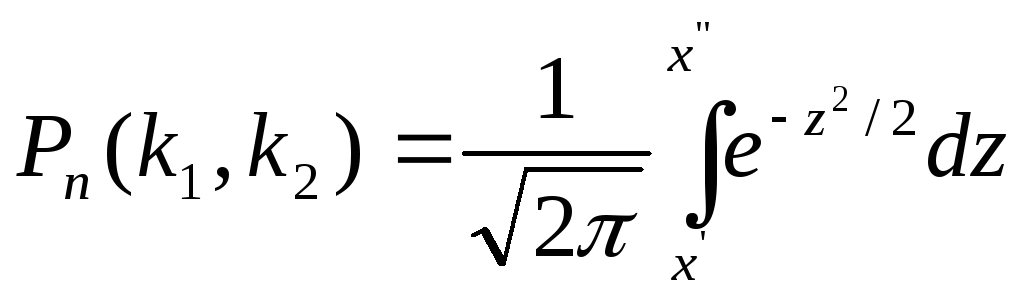
где

Таблица для интеграла приведена в приложении 2. Функцию называют функцией Лапласа. Она нечётна, т.е. .

Таким образом, искомая вероятность попадания числа наступлений события А в заданный интервал равна разности значений функции Лапласа:

Распределение Пуассона

Пусть производится независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятностипоявлений события в этих испытаниях используют формулу Бернулли. Есливелико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р0,1). В этих случаях (велико, р мало) прибегают к асимптотической формуле Пуассона:

.

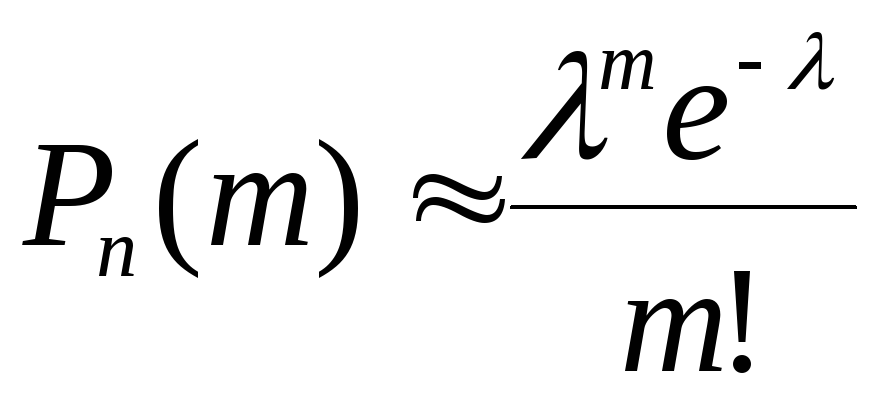Здесь сохраняет постоянное значение. Эта формула выражает закон распределения Пуассона вероятностей массовых (велико) редких (р мало) событий. Числоесть среднее число событий, которые появляются в единицу времени. Тогда вероятность того, что за времяt интересующее нас событие наступит ровно раз при заданномопределяется по формуле

.

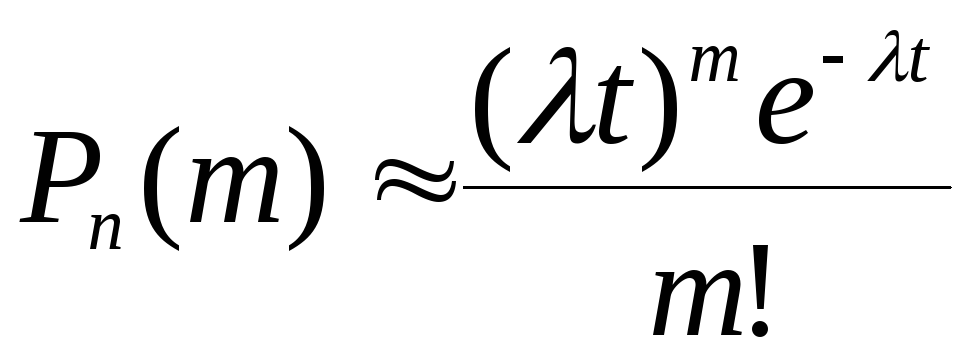Примеры решения задач типового расчета

Умножение вероятностей зависимых событий

Задача № 1

На десяти одинаковых карточках написаны различные цифры от 0 до 9. Определить вероятность того, что наудачу образованное из этих карточек 3-значное число делится на 5 (выборка без возвращения).

Решение

Первые две цифры могут быть любыми (первая отлична от 0), последней должен быть 0, либо 5. Следовательно, имеем одновременное выполнение трех условий, т.е. наступление трех событий, причем зависимых:

А – 1-я цифра любая, кроме 0;

В – 2-я цифра любая;

С – 3-я цифра 0, либо 5.

Тогда по теореме умножения вероятностей зависимых событий

.

Ответ: вероятность того, что образованное 3-значное число кратно 5 равна 0,225.

Задача № 2

За круглым столом 12 мест. 12 человек рассаживаются случайным образом. Найти вероятность того, что 2 определенных лица окажутся рядом.

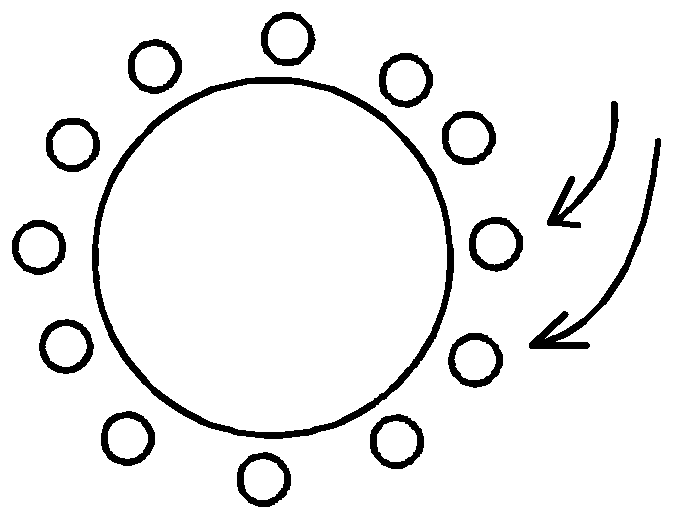
Решение

Обозначим событие А – 2 определенных лица сядут рядом – как произведение двух событий: В – 1-й человек занял место (он может сесть на любой стул) и С – 2-й человек сел рядом с первым. Тогда А=В ∙ С. События В и С зависимы, поэтому Р(А) = Р(В) ∙ Р_В(С).

Вероятность события В (1-й занял любое место) равна единице Р(В)=1

Вероятность события С при условии, что В произошло Р_В(С) определяем как (2-й может занять только 2 места из 11).

Тогда искомая вероятность Р(А) = Р(В) ∙ Р_В(С)=1∙=0,181.

Ответ: вероятность того, что 2 человека из 12 сядут рядом, равна 0,181.

Задача № 3

Слово М А Т Р О С разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово Р О С А.

Решение.

I способ

Интересующее нас событие А – извлеченные буквы образуют слово РОСА есть произведение 4-х зависимых событий:

А₁ – 1-я буква Р;

А₂ – 2-я буква О;

А₃ – 3-я буква С;

А₄ – 4-я буква А.

Тогда по теореме умножения вероятностей зависимых событий имеем

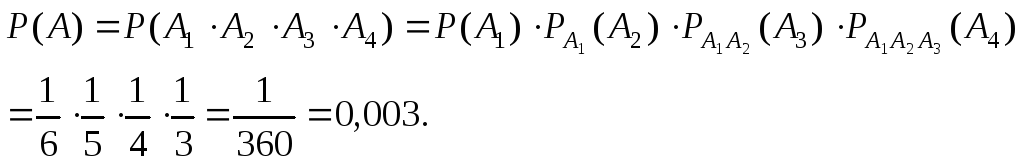
II способ

По классической формуле вероятности , гдеm – число благоприятных исходов, n – общее число исходов.

Тогда в условиях данной задачи m=1 (слово РОСА можно образовать единственным способом из данного набора букв),

Окончательно имеем .

Ответ: вероятность того, что наудачу взятые буквы образуют слово РОСА, равна 0,003.

Повторные независимые испытания, формула Бернулли.

Задача №4

Вероятность производства бракованной детали равна 0,008. Найти наивероятнейшее число бракованных среди 1000 деталей и вероятность такого количества их в партии.

Решение.

Наивероятнейшее число появлений события в n независимых испытаниях m₀ определяем из условия np - q ≤ m₀ < np + p.

Для нашей задачи n=1000, p=0,008, q=1-p=0,992.

Тогда 7,008 ≤ m₀ < 8,008. Этому условию удовлетворяет целое число m₀=8.

Найдем теперь вероятность того, что в партии из 1000 деталей равно 8 бракованных.

Поскольку число испытаний n=1000 достаточно велико, а p=0,008 достаточно мало, применим формулу Пуассона

,

где λ ≡ np – const – среднее число появлений события в одной серии испытаний.

Тогда ≈ 0,14 - вероятность того, что в партии из 1000 деталей ровно 8 бракованных.

Задача № 5

Найти вероятность того, что при 5 бросках игральной кости 6 очков не выпадет ни разу.

Решение.

Вероятность наступления события при n независимых испытаниях m раз, находим по формуле Бернулли

,

где p – вероятность появления интересующего нас события при одном испытании, q – вероятность противоположного события.

Тогда в условиях нашей задачи

(n=6, m=5, на верхней грани кубика любое число очков, кроме шести)

. Применяя формулу Бернулли, получим

Ответ: вероятность того, что при 5 бросках игральной кости 6 очков не выпадет ни разу, равна 0,3632.

Формула полной вероятности, формула Байеса.

Задача № 6

Имеются 4 урны с шарами. В первых трех по 1 белому и 1 черному, в четвертой - 4 белых и 1 черный.

1. Из наугад взятой урны достали шар. Найти вероятность того, что он белый.

2. Наугад вынутый шар оказался белым. Найти вероятность того, что он из четвертой урны.

Решение.

1. Пусть событие А состоит в том, что вынутый шар – белый. Это событие наступает в результате появления одного из двух несовместных событий (гипотез): В₁ – выбрали одну из первых трех урн;

В₂ – выбрали четвертую урну.

Очевидно, вероятности гипотез равны Р(В₁)=, Р(В₂)=.

Тогда, по формуле полной вероятности

.

Здесь - вероятность извлечь белый шар из урны с одним белым, одним черным шарами,- вероятность извлечь белый шар из четвертой урны.

Очевидно =,=.

2. Событие А уже произошло (вынули белый шар). Нужно найти так называемую переоцененную вероятность гипотезы В₂ - . Применяем формулу Байеса

.

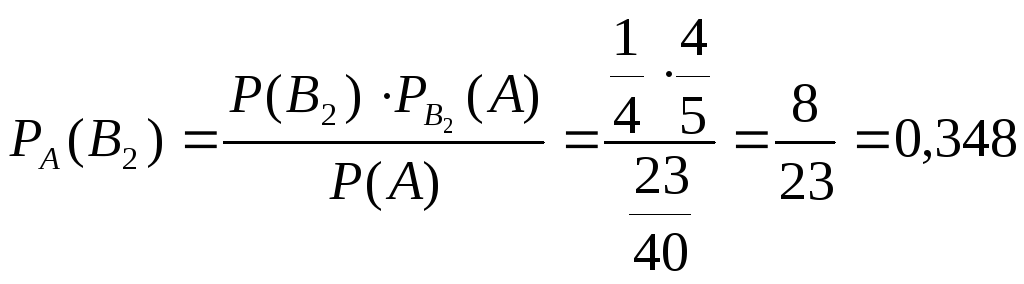Замечание: при сравнении переоцененной вероятности с безусловной убеждаемся, что они различны.

Ответ:

1. Вероятность того, что из наугад взятой урны достали белый шар, равна 0,575.

2. Вероятность того, что белый шар оказался из четвертой урны, равна 0,348.

Распределение Пуассона

Задача №7

Корректура в 400 страниц содержит 800 опечаток. Найти вероятность того, что наугад взятая страница содержит 3 опечатки.

Решение.

Находим среднее число опечаток на одной странице

Применяем формулу Пуассона для =3. Получаем, что искомая вероятность равна .

Локальная, интегральная теоремы Лапласа, теорема Бернулли.

Задача №8

Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение.

По условию, n=243; k=70; p=0,25; q=0,75. Так как n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:

, где .

Найдем значение x:

По таблице значений функции

найдем .

Искомая вероятность

Ответ: вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, равна 0,0231.

Задача №9

Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна p=0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

Решение.

Воспользуемся интегральной теоремой Лапласа:

где Ф(x) – функция Лапласа,

а) по условию, n=100; p=0,8; q=0,2; k₁=75; k₂=90. Вычислим x и x:

;

.

Учитывая, что функция Лапласа нечетна, т.е. Ф(-x)=-Ф(x), получим

.

По таблице значений функции найдем:

Ф(2,5)=0,4938; Ф(1,25)=0,3944.

Искомая вероятность

Р₁₀₀(75;90)=0,4938+0,3944=0,8882.

б) требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76, …, либо 100. Таким образом, в рассматриваемом случае следует принять k₁=75, k₂=100. Тогда

;

По таблице приложения 2 найдем Ф(1,25)=0,3944; Ф(5)=0,5.

Искомая вероятность

Р₁₀₀(75;100)=Ф(5)-Ф(-1,25)=Ф(5)+Ф(1,25)=0,5+0,3944=0,8944.

в) События – “А появилось не менее 75 раз” и “А появилось не более 74 раз” противовоположны, поэтому сумма вероятностей этих событий равна единице.

Следовательно, искомая вероятность Р₁₀₀(0;74)=1- Р₁₀₀(75;100)=1-0,8944=0,1056.

Задача №10

Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.

Решение.

По условию, n=625; p=0,8; q=0,2; =0,04.

Требуется найти вероятность

Воспользуемся формулой .

Имеем

.

По таблице приложения 2 найдем Ф(2,5)=0,4938. Следовательно, 2Ф(2,5)=2·0,4938=0,9876.

Ответ: искомая вероятность приближенно равна 0,9876.

Некоторые дополнительные задачи

Задача «О шарах»

В урне 2 белых, 3 черных, 1 красный шар. Наудачу извлекают 2 шара. Найти вероятность того, что это будут белый и черный шары.

Решение.

I способ (шары извлекаются последовательно).

Рассмотрим интересующее нас событие А - появление одного черного и одного белого шара – как сумму событий А₁ – первый шар белый, второй черный и А₂ – первый черный, второй белый.

Тогда А= А₁ + А₂, т.е. событие А состоит в появлении либо события А₁, либо события А₂.

В свою очередь, А₁ есть произведение (совместное наступление) событий В₁ и С₁:

В₁ – первым извлекли белый шар,

С₁ – вторым извлекли черный шар.

Поскольку В₁ и С₁ события зависимые, то P(A₁)=P(B₁) ∙ (C₁).

Найдем вероятность события B₁.

Всего шаров в урне шесть, из них 2 белых. Следовательно, вероятность извлечь белый шар равна 2/6.

Найдем (С₁). Событие С₁ наступает после события В₁, в урне осталось 5 шаров, из них 3 черных.

Следовательно, (С₁)=.

Тогда P(A₁)=P(B₁) ∙ (C₁)= .

Аналогично найдем вероятность события А₂ (сначала черный, потом белый).

Введем события В₂ и С₂:

В₂ ‑  первым появился черный шар,

С₂ – вторым появился белый шар.

Тогда P(B₂) = и искомая вероятность P(A₂)=P(B₂) ∙ (C₂)= .

Наконец, интересующая нас вероятность события А равна

P(A)=P(A₁) + P(A₂) = .

II способ (шары извлекаются одновременно)

Согласно классической формуле вероятности P=m/n, где m  -  число благоприятных исходов, n – общее число исходов.

Общее число n исходов опыта в данной задаче (извлечение двух шаров из шести возможных) определяется числом способов, какими можно извлечь два шара из шести. Это число сочетаний из шести по два, n=.

При этом благоприятное число исходов m =  - из двух белых извлекаем один {} способами и из трех черных извлекаем один {} способами.

Применяя формулу сочетаний , получим

. Окончательно, P=.

Ответ: вероятность того, что из двух извлеченных наудачу шаров будет один белый и один черный, равна .

Задача «О лгунах»

В городе N жителей. Некто пустил слух, рассказав «новость» 1-му жителю. Тот рассказал следующему и т.д. Какова вероятность того, что 10-й житель расскажет «новость» тому, кто узнал ее первым.

Решение.

Для того, чтобы произошло интересующее нас событие А – 10-й житель рассказал «новость» первому, необходимо, чтобы первые девять этого не сделали. Очевидно, что первые два жителя из этих девяти не сделают этого с вероятностью, равной единице.

Остальные семь – с вероятностью, равной . Десятый же расскажет «новость» первому с вероятностью, т.к. благоприятный исход один, общее -N-2, поскольку в общем случае новость рассказывается любому жителю из N за исключением того, от кого услышана.

Таким образом, искомая вероятность определяется как .