
Кристаллография / Лекции_по_кристаллографии_посл_вар_2
.2.pdf31
параллелепипедов, и, таким образом, на каждый параллелепипед приходится одна восьмая часть от каждого из восьми узлов. Однако в физике твердого тела принято выбирать примитивную ячейку обратной решетки в виде ячейки наименьшего объема, каждая грань которой проходит через середину
соответствующего вектора |
G , имеющего минимальную длину, |
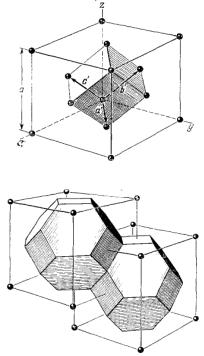
перпендикулярно к нему. Каждая из этих (новых) ячеек содержит один узел решетки, который расположен в центре ячейки. Указанная ячейка представляет собой ячейку Вигнера—Зейтца для обратной решетки, и она является первой зоной Бриллюэна ОЦК решетки. Грани этой зоны перпендикулярны к двенадцати векторам, определяемым выражениями (4.16), и проходят через их середины. Зона имеет вид правильного двенадцатигранника — ромбододекаэдра (рис. 4.6). Векторы, проведенные из начала координат к центру каждой из граней, - это половины векторов, определяемых выражениями (4.16), или
π |
±x±y ; |
π |
± y±z ; |
π |
±x±z . |
(4.17) |
a |
|
a |
|
a |
|
|
Поскольку выбор знаков независим, общее число векторов — двенадцать. Обратная решетка ГЦК решетки. Векторы примитивных трансляций ГЦК
решетки, показанные на рис. 4.6, равны |
|
|
|||||
a'= 1 a x y ; b'= 1 a y z ; |
c'= 1 a x z . |
(4.18) |
|||||
2 |
|
2 |
|
|
2 |
|
|
Эти векторы параллельны векторам a* , |
b* , c* (4.1). Объем примитивной |
||||||
элементарной ячейки |
|
|
1 |
|
|
|
|
V= a' b' ×,c' = |
a3 |
(4.19) |
|||||
|
|||||||
|
|
4 |
|
|
|
||
По определению (4.12) векторы примитивных трансляций |
a* , b* , c* |
||||||
обратной решетки для ГЦК решетки таковы: |
|
||||||
a*= |
2π x y −z ; |
|
|||||
|
|
a |
|
|
|||
b*= |
2π |
; |
|
||||
|
a −x y z |
(4.20) |
|||||
|
|
|
|
|
. |
||
c*= |
2π x− y z . |
|
|||||
|
|
a |
|
|
|||
Это векторы примитивных трансляций ОЦК решетки. Следовательно, ОЦК решетка является обратной для ГЦК решетки. Объем примитивной элементарной ячейки обратной решетки равен
a* b* ×c*=4 2π/a 3 . |
(4.21) |
Для векторов обратной решетки получаем следующее общее выражение:
32
G= 2π |
[ h−k+l x h+k −l y −h+k+l z ] , |
(4.22) |
|
|
a |
|
|
где h , k , |
l |
— произвольные целые числа. Кратчайших отличных от нуля |
|
векторов G |
— восемь |
|
|
|
|
2π ±x± y±z . |
(4.23) |
|
|
a |
|
Рис. 4.7. Примитивные базисные векторы ГЦК решетки
Рис. 4.8. Зоны Бриллюэна ГЦК решетки. Изображены ячейки в обратном пространстве. Видно, что обратная решетка является объемноцентрированной кубической решеткой
Примитивная ячейка обратной решетки почти полностью ограничивается восемью плоскостями, перпендикулярными к указанным векторам и проходящими через их середины. Однако вершины такого октаэдра оказываются срезанными плоскостями, которые перпендикулярны к другим шести векторам обратной решетки
2π |
±2 x |
; |
2π |
±2 y ; |
2π |
±2 z . |
(4.24) |
a |
|
|
a |
|
a |
|
|
33
и делят эти векторы пополам. Таким образом, примитивная ячейка является ближайшей к началу координат ячейкой с наименьшим объемом и представляет собой усеченный октаэдр, показанный на рис. 4.8. Это и есть первая зона Бриллюэна ГЦК решетки.
34
Лекция 5
Кристаллографические проекции
Представление кристаллографического пространства в виде совокупностей взаимно параллельных узловых плоскостей и узловых рядов, среди которых есть плоскость или ряд, проходящие через начало координат, позволяет описать кристаллическую решетку в виде множества узловых плоскостей и узловых рядов, пересекающихся в одной точке. Аналогично, грани и ребра кристаллического многогранника, которые всегда параллельны соответствующим узловым плоскостям и узловым рядам решетки, можно изображать пересекающимися хотя бы в одной точке.
В кристаллографии разработаны удобные и информативные методы изображения на чертеже таких прямых и плоскостей. Подобные изображения получили названия кристаллографических проекций.
Важнейшей характеристикой взаимного расположения узловых плоскостей и узловых рядов, а также граней и ребер внешней огранки кристалла являются углы между ними. Поэтому кристаллографические проекции должны позволить работать с углами, которые характеризуют взаимное расположение прямых и плоскостей, отвлекаясь от геометрических размеров конкретного кристаллического образца.
Для построения кристаллографической проекции кристаллического многогранника перенесем все грани и ребра параллельно самим себе так, чтобы они пересекались в одной точке пространства O. К каждой грани из той же точки восстановим нормали, которые будут определять ориентацию соответствующих плоскостей. Построенная совокупность прямых и плоскостей
называется кристаллическим комплексом, а выбранная таким образом точка О
– центром кристаллического комплекса.
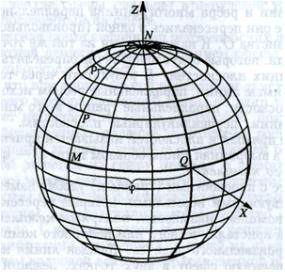
Сферическая проекция. Из центра кристаллического комплекса описывается сфера произвольного радиуса. Точка пересечения линии комплекса с поверхностью сферы есть сферическая проекция направления. Для представления сферических проекций в числовой форме вводят сферическую систему координат или, иначе говоря, систему полярных координат на поверхности сферы (рис. 5.1). Для этого построим прямую, проходящую через центр сферы и называемую полярной осью. Точка, в которой положительная
полярная полуось пересекает сферу, называется северным полюсом N . Противоположная точка сферы называется южным полюсом S . Дуги больших
кругов, соединяющих полюса, по аналогии с геодезической проекцией, называют меридианами. Через каждую точку сферы (за исключением обоих полюсов) можно провести только один меридиан.
35
Рис. 5.1. Сферическая система координат: |
Р |
— произвольная точка на |
|
поверхности сферы с полярным углом ρ и азимутом |
; M — точка на |
||
экваторе с азимутом р и полярным углом ρ |
= 900 ; Q |
— точка на экваторе |
|
с нулевым азимутом; N — северный полюс сферы, южный полюс не виден |
|||
Первая сферическая координата – долгота |
|
– отсчитывается по экватору |
|
от нулевого индекса по часовой стрелке (на сетке каждое деление соответствует 2°, каждый десятый градус выделен жирной линией).
Вторая сферическая координата – полярное расстояние ρ – отсчитывается по любому направлению от нуля (северный полюс N ) до 1800 (южный полюс
S).
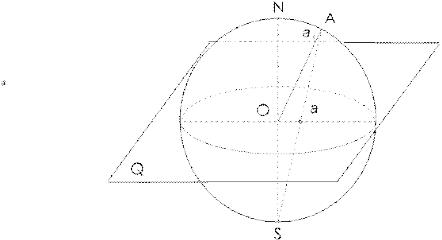
Стереографическая проекция. Плоскостью проекции является
экваториальная плоскость Q . Для построения стереографической проекции
прямой, например OA , проводят линию AS |
на сфере от точки A на сфере |
проекций до южного полюса S сферы. Точка |
a пересечения линии AS с |
кругом проекции есть стереографическая проекция направления OA .
36
Рис. 5.2. Построение стереографической проекции
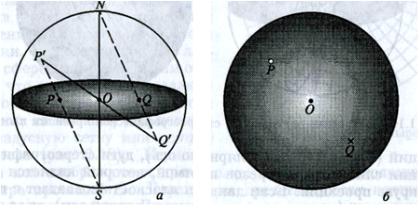
Построим стереографическую проекцию прямой линии, проходящей через центр сферы О . Любая подобная прямая пересекает сферу в двух диаметрально противоположных точках Р' и Q' . Существенно, что эти точки всегда лежат в различных полушариях. Соединим каждую из точек Р' и Q' отрезками с противоположными полюсами. Точки Р и Q пересечения
этих отрезков с плоскостью проекций называются стереографической проекцией данной прямой (рис. 5.3а).
В практической работе со стереографическими проекциями различают точки, спроецированные с различных полушарий сферы, обозначая их различными значками. Например, стереографические проекции точек, лежащих на северном полушарии, можно обводить кружками, а стереографические проекции точек южного полушария изображать крестиками. Тогда прямая,
проходящая через центр О , изобразится на стереографической проекции кружком и крестиком, лежащими на одном диаметре и равноотстоящими от центра круга проекций О (см. рис. 5.3). В частном случае, когда прямая
перпендикулярна полярной оси (лежит в плоскости проекций), ее стереографическая проекция изображается двумя точками, которые находятся на концах диаметра круга проекций. В этом случае точки стереографической
проекции Р и Q совпадают с проецируемыми точками сферы Р' и Q' . Если прямая совпадает с полярной осью, то точки ее стереографической проекции (кружок и крестик) сливаются с центром проекций О .
37
Рис. 5.3. Построение (а) и вид (б) стереографической проекции прямой линии:
Р' |
и |
Q' |
— точки пересечения прямой линией поверхности сферы. Точка |
|||
О |
— центр сферы, точки N |
и S |
— северный и южный полюса сферы. |
|||
Точки |
Р |
и Q |
лежат в |
плоскости круга проекций и являются |
||
стереографическими проекциями точек |
Р' и Q' соответственно |
|||||
При построении стереографической проекции плоскости следует провести отрезки от полюсов N и S в принципе к каждой точке окружности, по
которой пересекается данная плоскость со сферой. Пересечения отрезков с плоскостью проекций дадут множество точек, которое и является стереографической проекцией плоскости. Следовательно, стереографическая проекция плоскости состоит из двух симметричных дуг, кривизна которых зависит от угла наклона плоскости к полярной оси (рис. 5.4).
В частном случае, когда изображаемая плоскость перпендикулярна плоскости проекций (т. е. содержит полярную ось), дуги стереографической проекции сливаются в отрезок прямой, который является диаметром круга проекций. Если данная плоскость совпадает с плоскостью проекций (т. е. перпендикулярна полярной оси), то ее стереографическая проекция совпадает с окружностью, ограничивающей круг проекций.
Следует различать проекции частей окружности, находящихся в северной и южной частях сферы. Одна часть стереографической проекции плоскости будет состоять из кружков, вторая — из крестиков.
Также можно эти дуги изображать, например, сплошной и штриховой линиями соответственно.
38
Рис. 5.4. Построение (а) и вид (б) стереографической проекции плоскости
Рис. 5.5. Построение стереографической проекции кристалла
Все точки стереографической проекции связаны взаимно однозначным
39
соответствием с точками поверхности сферы. Поэтому каждая точка стереографической проекции может быть охарактеризована сферическими
координатами ρ и . Для быстрого и удобного определения сферических
координат точек стереографической проекции используются специальные шаблоны, называемые градусными сетками.
На рис. 5.5 показано построение стереографической проекции кристалла, а
на нижнем рис. - сама проекция. |
|
|
|
|
Гномостереографическая |
проекция. |
Чтобы |
получить |
|
гномостереографическую |
проекцию |
кристаллографической |
плоскости, |
|
проводят нормаль к этой плоскости до пересечения со сферой проекций, а затем линию, соединяющую эту точку пересечения и южный полюс сферы. Гномостереографическая проекция плоскости является точка. Гномостереографические проекции направлений изображаются дугами больших кругов.
Рис. 5.6. Связь между стереографической и гномостереографической проекциями
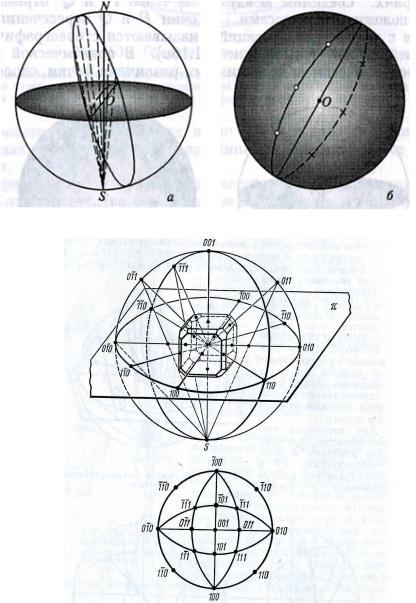
Гномоническая проекция. Плоскость гномонической проекции – касательная к северному полюсу сферы проекций. Проекция направления OA дает на сферической проекции точку a , определенную координатами , ρ , на
гномонической проекции – точку a2 , на стереографической проекции – точку
a1 .
Для удобства построения проекций используются специальные

40
стереографические сетки (например, «сетка Болдырева», рис. 5.7a), наибольшее распространение из которых получила в кристаллографии сетка Вульфа (рис. 5.7б), предложенная русским ученым Г.В. Вульфом в 1897 году. Она представляет собой стереографическую проекцию градусной сети сферы на меридиональную плоскость. Стандартный радиус сетки – 100 мм, цена деления
– 2°.
Таблица 5.1
Соотношения между различными типами проекций
Тип проекции |
Изображение |
|
|
|
|
|
плоскости |
прямой |
|
|
|
Стереографическая |
Дуга большого круга |
Точка |
|
|
|
Гномостереографичес |
Точка |
Дуга большого круга |
кая |
|
|
Гномоническая |
Точка |
Прямая |
С помощью сетки Болдырева легко откладывать и считывать сферические координаты точек, однако сложно графически измерить угловые расстояния
между произвольными точками А и В на стереографической проекции.
Поэтому на практике чаще используется другой шаблон, называемый сеткой Вулъфа или экваториальной градусной сеткой.
Методы решения различных количественных задач кристаллографии с помощью стереографической проекции основаны на двух важных ее свойствах.
Свойство 1. Окружность на поверхности сферы отображается на стереографическую проекцию тоже в виде окружности.
Свойство 2. Угол между дугами больших кругов на сфере равен углу между стереографическими проекциями этих дуг.
