
Кристаллография / Лекции_по_кристаллографии_посл_вар_2
.2.pdf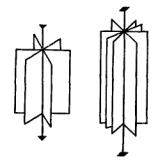
61
совмещают каждую из плоскостей последовательно со всеми остальными 2р плоскостями, так что все плоскости симметрии эквивалентны и отражения в них входят в один класс. Среди поворотов вокруг оси имеется 2р операций, отличных от тождественной, которые попарно сопряжены друг с другом,
образуя р классов по два элемента ( C k2p 1 и C−2pk 1 k=1,2,. . . ,р ); кроме того, e составляет еще один отдельный класс. Таким образом, имеется всего р+ 2 классов.
Рис 8.1. Группы C 3v и C 4v
Если же n четно ( n= 2р ), то последовательными поворотами C 2p
можно совместить лишь чередующиеся через одну плоскости; две соседние плоскости не могут быть совмещены друг с другом. Таким образом, имеются
два набора по р эквивалентных плоскостей и соответственно два класса по р элементов (отражений) в каждом. Что касается поворотов вокруг оси, то
составляют каждый сам по себе класс, а остальные
2р−2 поворотов попарно сопряжены и дают еще |
р −1 |
классов по два |
|||||||||
элемента. Всего группа |
C 2p,v |
имеет, следовательно, |
р+ 3 |
классов. |
|
||||||
V. Группы D n |
|
n |
|
|
|
|
|
|
|
|
|
Если к оси симметрии |
-ого порядка присоединить перпендикулярную ей |
||||||||||
ось второго порядка, то это приведет к появлению еще |
n−1 |
таких же осей, |
|||||||||
так что будет всего n |
горизонтальных осей второго порядка, пересекающихся |
||||||||||
под углами |
π /n . Получающаяся группа |
D n |
содержит |
2n |
элементов: n |
||||||
поворотов |
вокруг оси |
n |
-го порядка и |
n |
поворотов |
на угол π |
вокруг |
||||
горизонтальных осей |
(условимся обозначать |
последние |
посредством |
U 2 , |
|||||||
оставив обозначение C 2 |
для поворота на угол π |
вокруг вертикальной оси). |
|||||||||
62
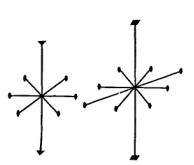
На рис. 8.2 изображены в качестве примера системы осей групп D3 и D 4 .
Совершенно аналогично предыдущему случаю, убеждаемся, что ось n -го порядка является двусторонней, а горизонтальные оси второго порядка все эквивалентны, если n нечетно, или образуют два неэквивалентных набора,
если n четно. Следовательно, группа |
D 2p |
имеет следующие |
р+ 3 |
классов: |
|||||
e , 2 класса по р поворотов U 2 |
в каждом, поворот |
C 2 |
и |
р−1 |
классов |
||||
по два поворота вокруг вертикальной оси. Группа же |
D 2p 1 |
имеет |
р+ 2 |
||||||
классов: e , 2р 1 |
поворотов |
U 2 |
и р |
классов по два поворота вокруг |
|||||
вертикальной оси. |
|
|
|
группа D 2 . |
|
|
|
|
|
Важным частным |
случаем является |
Ее |
система |
осей |
|||||
складывается из трех взаимно перпендикулярных осей второго порядка. Эту группу обозначают также посредством V .
Рис. 8.2. Группы |
D3 и D 4 |
VI. Группы D nh |
системе осей группы D n горизонтальную плоскость |
Если добавить к |
симметрии, проходящую через n осей второго порядка, то при этом автоматически появится n вертикальных плоскостей, каждая из которых проходит через вертикальную ось и одну из горизонтальных осей. Получающаяся при этом группа D nh содержит 4n элементов; кроме 2n
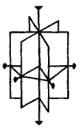
элементов группы D n в нее входят еще n отражений m v и n зеркальноповоротных преобразований C kn mh . На рис. 8.3 изображена система осей и плоскостей группы D 3h .
63
|
Рис. 8.3. Группа D 3h |
|
|
|
|
|
|
|
|||
Отражение |
m h |
коммутативно со всеми остальными элементами группы; |
|||||||||
поэтому можно написать D nh |
в виде прямого произведения |
D nh =Dn×C s . |
|||||||||
При четном n |
в числе элементов группы имеется инверсия, и можно написать |
||||||||||
также |
D 2p,h=D 2p×C i . |
|
|
|
D nh |
|
|
|
|||
Отсюда следует, что число классов в группе |
равно удвоенному числу |
||||||||||
классов в группе D n . Половина из них совпадает с классами группы |
D n |
||||||||||
(повороты вокруг осей), а остальные получаются из них умножением на |
m h . |
||||||||||
Отражения |
m v |
в вертикальных плоскостях относятся все к одному классу |
|||||||||
(если |
n |
нечетно) |
или образуют |
два |
класса (при |
четном |
n ). Зеркально- |
||||
поворотные преобразования |
m h C nk |
и |
m h C−n k |
попарно сопряжены друг с |
|||||||
другом. |
|
D nd |
|
|
|
|
|
|
|
|
|
VII. Группы |
|
|
|
|
|
|
D n можно еще |
||||
Присоединить плоскости симметрии к системе осей группы |
|||||||||||
одним способом. Именно, можно провести их вертикально через ось n |
-ого |
||||||||||
порядка посредине между каждыми двумя соседними горизонтальными осями второго порядка. Опять присоединение одной такой плоскости влечет за собой
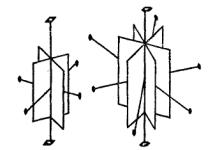
появление еще плоскостей. Получающаяся система осей и плоскостей симметрии определяет группу D nd (на рис. 8.4 изображены оси и плоскости групп D 2d и D 3d ).
64
Рис. 8.4. Группы D 2d и |
D 3d |
|
||
Группа |
D nd |
содержит |
4n элементов. К 2n элементам группы D n |
|
присоединяется n |
отражений в вертикальных плоскостях (обозначаемых |
|||
посредством |
m d |
— «диагональные» плоскости) и n |
преобразований вида |
|
G=U 2 md . Для |
того чтобы выяснить характер последних, замечаем, что |
|||
поворот U 2 |
можно написать в виде U 2 =mh mv , где |
m v — отражение в |
||
вертикальной плоскости, проходящей через данную ось второго, порядка; тогда
G=mh mv mh |
(преобразований m v |
, |
m h |
самих по себе в числе элементов |
||||||
группы, разумеется, нет). Поскольку плоскости отражений |
m v |
и m d |
||||||||
пересекаются |
друг |
с |
другом |
вдоль |
оси |
n -ого порядка, образуя угол |
||||
π /2n 2k 1 , |
где |
k = 1 ,..., |
n−1 |
(поскольку здесь |
угол |
между |
||||
соседними плоскостями равен |
π /2n ), то, |
m v md =C 2n2k+1 . Таким образом, |
||||||||
находим, что |
G=mh C 2n2k 1=S 2n2k+1 |
, т. е. эти элементы представляют собой |
||||||||
зеркально-поворотные |
преобразования |
вокруг |
вертикальной |
оси, |
||||||
оказывающейся, следовательно, не простой осью симметрии n -ого порядка, а зеркально-поворотной осью 2n -ого порядка.
Диагональные плоскости отражают две соседние горизонтальные оси второго порядка друг в друга; поэтому в рассматриваемых группах все оси
второго порядка эквивалентны (как при четных, так и при нечетных n ). Аналогично, эквивалентны все диагональные плоскости. Зеркально-поворотные
преобразования S2k2n 1 и S−2n2k−1 попарно сопряжены друг с другом.
Применяя эти соображения к группе |
D 2p,d |
, находим, |
что она содержит |
следующие 2р 3 классов: e , поворот |
C 2 |
вокруг оси |
n -ого порядка, ( |
р −1 ) классов по два сопряженных поворота вокруг той же оси, класс 2р поворотов U 2 , класс 2р отражений m d и р классов по два зеркально-
65
поворотных преобразования.
При нечетном n ( n= 2р 1 ) в числе элементов группы имеется инверсия (это видно из того, что одна из горизонтальных осей в этом случае
перпендикулярна |
к |
вертикальной |
плоскости). |
Поэтому |
можно |
написать |
|
D 2p 1,d =D2p+1×C i |
, так что группа |
D 2p 1,d |
содержит |
2р 4 |
классов, |
||
получающихся непосредственно из |
р+ 2 |
классов группы D 2p 1 . |
|
||||
VIII. Группа T |
(группа тетраэдра) |
|
|
|
|
||
Система осей этой группы есть система осей симметрии тетраэдра. Она может быть получена добавлением к системе осей группы V четырех
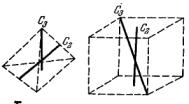
наклонных осей третьего порядка, повороты вокруг которых переводят три оси второго порядка друг в друга. Эту систему осей удобно представить, изображая три оси второго порядка как проходящие через центры противоположных граней куба, а оси третьего порядка — как пространственные диагонали этого куба. На рис. 8.5 изображено расположение этих осей в кубе и в тетраэдре (по одной оси каждого типа).
Рис 8.5. Система осей группы тетраэдра
Три оси второго порядка эквивалентны между собой. Оси третьего порядка тоже эквивалентны, так как переводятся друг в друга поворотами C 2 , но они не являются двусторонними осями. Отсюда следует, что 12 элементов в группе T распределяются по четырем классам: e , три поворота C 2 , четыре
поворота C 3 и четыре поворота C 23 .
IX. Группa T d
Эта группа содержит все преобразования симметрии тетраэдра. Систему ее осей и плоскостей можно получить, добавляя к осям группы T плоскости
симметрии, каждая из которых проходит через одну ось второго и две оси третьего порядков. При этом оси второго порядка становятся зеркальноповоротными осями четвертого порядка (подобно тому как это имеет место в
группе D 2d . Эту систему удобно представить, изображая три зеркально-
поворотные оси проходящими через центры противоположных граней куба, четыре оси третьего порядка, как его пространственные диагонали, шесть

66
плоскостей симметрии проходящими через каждую пару противоположных ребер (на рис. 8.6 изображено по одному из каждого рода осей и плоскостей).
Рис. 8.6. Элементы симметрии группы T d
Поскольку плоскости симметрии вертикальны по отношению к осям третьего порядка, то последние являются двусторонними осями. Все оси и плоскости каждого рода эквивалентны. Поэтому 24 элемента группы
распределяются по следующим 5 классам: e , восемь поворотов C 3 и C 23 , шесть отражений в плоскостях, шесть зеркально-поворотных преобразований
S4 и |
S43 , три поворота C 2 =S 42 . |
|
|
||
X. Группа T h |
|
из T |
|
|
|
Эта |
группа |
получается |
добавлением |
центра симметрии |
|
T h =T ×C i . В |
результате |
появляются |
три взаимно |
перпендикулярные |
|
плоскости симметрии, проходящие через каждые две оси второго порядка, а оси третьего порядка становятся зеркально-поворотными осями шестого порядка (на рис. 8.7 изображено по одной из этих осей и плоскостей).
Рис. 8.7. Элементы симметрии группы T h
Группа содержит 24 элемента, распределенных по 8 классам, непосредственно получающимся из классов группы T .

67
XI. Группа O (группа октаэдра)
Системой осей этой группы является система осей симметрии куба: три оси четвертого порядка проходят через центры противоположных граней, четыре оси третьего порядка — через противоположные вершины и шесть осей второго порядка — через середины противоположных ребер (рис. 8.8).
Рис. 8.8. Система осей группы октаэдра
Легко видеть, что все оси одинакового порядка эквивалентны и каждая из них - двусторонняя. Поэтому 24 элемента распределяются по следующим 5
классам: |
e , восемь поворотов С 3 и С 32 , шесть поворотов С 4 и С 43 , три |
поворота |
С 42 и шесть поворотов С 2 . |
XII. Группа O h
Это есть группа всех преобразований симметрии куба. Она получается
добавлением к группе O |
центра симметрии: |
O h =O×C i . Оси |
третьего порядка группы |
превращаются при |
этом в зеркально- |
поворотные оси шестого порядка (пространственные диагонали куба); кроме того, появляются еще шесть плоскостей симметрии, проходящих через каждую пару противоположных ребер, и три плоскости, параллельные граням куба (рис. 8.9).
Рис. 8.9. Элементы симметрии группы O h
68
Группа содержит 48 элементов, распределенных по 10 классам, которые могут быть непосредственно получены из классов группы O . Именно, 5 совпадают с классами группы O , а остальными являются:
I ; восемь зеркально-поворотных преобразований S6 и S56 ; шесть
зеркально-поворотных |
преобразований |
C 4 mh , С 43 mh вокруг |
осей |
|
четвертого порядка; три отражения |
m h |
в плоскостях, горизонтальных |
||
по отношению к осям |
четвертого |
порядка; шесть отражений |
m v в |
|
плоскостях, вертикальных по отношению к этим осям. XIII, XIV. Группы Y , Y h (группы икосаэдра)
Эти группы осуществляются в природе в качестве групп симметрии молекул лишь в исключительных случаях. Поэтому мы ограничимся
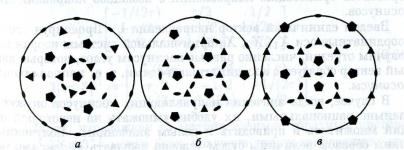
здесь указанием, что Y есть группа 60 поворотов вокруг осей
симметрии икосаэдра (правильного 20-гранника с треугольными гранями) или пентагонального додекаэдра (правильного 12-гранника с пятиугольными гранями), причем имеется 6 осей пятого порядка, 10 —
третьего и 15 — второго. Группа Y h получается добавлением центра
симметрии: Y h =Y ×C i , и представляет собой полную группу преобразований симметрии указанных многогранников.
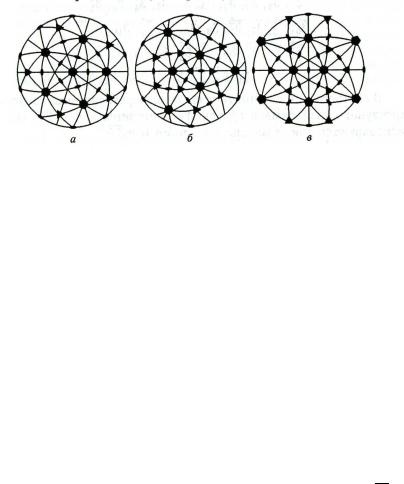
Рис. 8.10. Стереографическая проекция группы Y :
а – плоскость проекции перпендикулярна оси 5-го порядка, б – оси 3-ого порядка и в – оси второго порядка
В кристалле могут существовать только оси 1,2, 3, 4 и 6 порядков. Другие типы преобразования связаны с действием центра инверсии. Центром инверсии называется такое преобразование, при котором каждое направление и плоскость заменяются на обратные. При этом
69
правая система координат меняется на левую. Действие центра инверсии может быть совмещено с действием оси симметрии, при этом результирующий элемент симметрии называется инверсионной осью симметрии. Также, как и для поворотных, в кристаллах возможны
Рис. 8.11. Стереографическая проекция группы Y h :
а – плоскость проекции перпендикулярна оси 5-го порядка, б – оси 3-ого порядка и в – оси второго порядка
только инверсионные оси симметрии 1, 2, 3, 4 и 6 порядков. Инверсионную ось симметрии первого порядка называют центром
симметрии.
Инверсионная ось второго порядка является плоскостью симметрии. Действие инверсионной оси нечетного порядка может быть рассмотрено как комбинация центра симметрии и поворотной оси
такого же порядка Инверсионная ось четного порядка содержит поворотную ось вдвое
меньшего порядка.
При обозначении элементов симметрии используются три системы обозначений – символика Бравэ, международная и графическая символика, предназначенная для использования на стереографических проекциях. В международной системе для обозначения
кристаллографических классов (точечных групп) приняты: n – ось симметрии n -ого порядка, n – инверсионная ось симметрии n -ого порядка, m – плоскость симметрии, nm – ось симметрии n -ого
n
порядка и n плоскостей симметрии, проходящих вдоль нее, m – ось
симметрии порядка n и плоскость симметрии, перпендикулярная к ней, n2 – ось симметрии порядка n и n осей второго порядка,
|
|
|
|
|
70 |
|
|
|
перпендикулярных к ней, |
n m |
или n /mmm |
– ось симметрии |
n -ого |
||||
|
|
|
|
m |
|
|
|
|
порядка и плоскости, параллельные и перпендикулярные к ней. |
|
|||||||
|
|
|
|
|
|
|
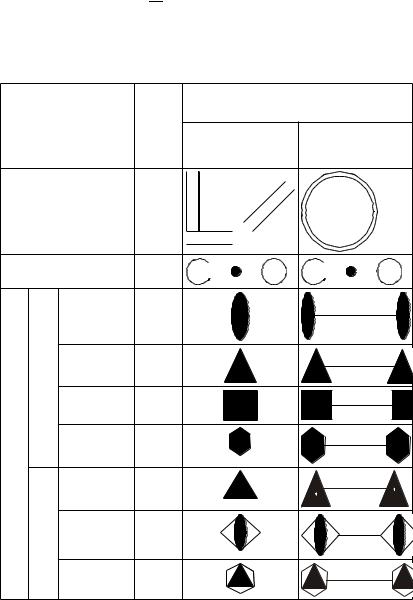
Таблица 8.1 |
|
|
Элементы симметрии конечных фигур и их обозначения |
|
||||||
Название |
|
|
Обозн |
Изображение |
по |
отношению |
к |
|
|
|
|
|
ачение |
плоскости чертежа |
|
|
|
|
|
|
|
между |
перпендикулярное |
параллельное |
|
|
|
|
|
|
народн |
|
|
|
|
|
|
|
|
ое |
|
|
|
|
Плоскость симметрии |
|
|
|
|
|
|
||
Центр симметрии |
|
|
|
|
|
|
||
Ос |
пов |
двойная |
|
|
|
|
|
|
и |
орт |
|
|
|
|
|
|
|
си |
ные |
|
|
|
|
|
|
|
мм |
|
тройная |
|
|
|
|
|
|
етр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ии |
|
|
|
|
|
|
|
|
|
|
четвертная |
|
|
|
|
|
|
|
|
шестерная |
|
|
|
|
|
|
|
инв |
тройная |
|
|
|
|
|
|
|
ерс |
|
|
|
|
|
|
|
|
ион |
четвертная |
|
|
|
|
|
|
|
ные |
|
|
|
|
|
|
|
|
|
шестерная |
|
|
|
|
|
|
Классом симметрии |
называется множество |
элементов симметрии, |
||||||
