Кристаллография / Лекции_по_кристаллографии_посл_вар_2

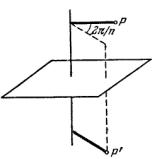
51

кратное повторение зеркально-поворотного преобразования будет равносильно простому отражению в плоскости, перпендикулярной к оси (поскольку угол

поворота будет равен 2π , а нечетное число отражений в одной и той же плоскости есть простое отражение). Повторяя это преобразование еще n раз, найдем в результате, что зеркально-поворотная ось сводится к одновременному наличию независимых оси симметрии n -го порядка и перпендикулярной к ней плоскости симметрии. Если же n — четное число, то n -кратное повторение зеркальноповоротного преобразования возвращает тело в исходное положение. Зеркальноповоротное преобразование обозначаем символом Sn .

Рис. 7.1. Зеркально-поворотное преобразование

Важным частным случаем является зеркально-поворотная ось второго порядка. Легко сообразить, что поворот на угол π с последующим отражением в плоскости, перпендикулярной к оси вращения, представляет собой преобразование инверсии,

относительно этого преобразования, говорят, что оно обладает центром симметрии. Операцию инверсии мы будем обозначать символом I ; имеем

I ≡S 2 .

Помимо наглядного геометрического описания симметрии с помощью элементов симметрии широко применяется теория групп. Ее методы основаны на том замечательном обстоятельстве, что операции симметрии физических систем и геометрических объектов могут комбинироваться друг с другом, лишь образуя замкнутые множества, которые называются группами.

Пусть имеется множество G однотипных (т. е. имеющих общие характерные признаки) элементов

Элемент е называется единичным (тождественным) элементом группы

G.

3.Для каждого элемента gi можно найти элемент, обозначаемый обычно

через g−i 1 , принадлежащий тому же множеству G , такой, что

Перечисленные свойства множества G , определяющие его как группу, часто

называются групповыми постулатами.

В общем случае «умножение» элементов группового множества некоммутативно. Если же все элементы группы коммутируют друг с другом, то группа называется абелевой. Множество G может быть дискретным (конечным или бесконечным) и непрерывным. В соответствии с этим различают дискретные и непрерывные группы. Если количество элементов группового множества равно некоторому числу, то группа называется конечной. Количество элементов конечной группы называется ее порядком. При бесконечном числе элементов группового множества группа

53

называется бесконечной.

Часто группы содержат подмножества, которые в свою очередь являются группами относительно той же операции «умножения». Такие подмножества называются подгруппами. Очевидно, что любая группа имеет две тривиальные подгруппы — подгруппу, множество которой состоит лишь из единичного элемента

е , и подгруппу, тождественную самой группе.

Пусть некоторая группа G порядка n содержит нетривиальную подгруппу

Термин «левый» является существенным, так как в общем случае умножение элементов группового множества некоммутативно. Правым смежным классом

Очевидно, что оба смежных класса являются подмножествами группового множества G, так как оба класса были получены перемножением элементов группы

G .

Любую группу G можно разложить по подгруппе R , представив ее

групповое множество в виде объединения элементов правых или левых смежных классов:

Правые и левые смежные классы по подгруппе в общем случае не совпадают. Если же разложения на правые и левые смежные классы по некоторой подгруппе

54

совпадают, то такая подгруппа называется инвариантной или нормальным делителем.

Это приводит к понятию «класса», в котором все элементы сопряжены друг другу. При этом ни один элемент не может принадлежать более чем к одному классу.

g j - любой элемент подгруппы G . Если, кроме того, любой элемент группы K может быть записан единственным образом в виде произведения hi g j , то группу K называют «прямым произведением» групп H и G , изображая это как K=H ×G . Данное определение означает, что единственным общим элементом групп H и G является единичный элемент.

Одним из наиболее полных способов описания конечной группы является ее представление в виде таблицы умножения, которая иногда называется квадратом Кэли. Чтобы получить квадрат Кэли для группы, строят квадратную таблицу, в первой строке и первом столбце которой записываются все элементы группового множества. На пересечении каждой строки и столбца записывается элемент группы, являющийся результатом умножения соответствующих элементов, находящихся в первой строке и первом столбце.

Рассмотрим несколько примеров групп.

Пример 1. Пусть G - множество всех целых чисел Z . В качестве

«умножения» зададим операцию сложения чисел. Покажем, что данное множество является группой. Очевидно, что множество всех целых чисел замкнуто относительно операции сложения, так как сумма любых целых чисел в свою очередь является целым числом. Проверим выполнение для данного множества групповых постулатов. Как известно, сложение чисел всегда ассоциативно. Единичным элементом является ноль, а каждому целому числу можно поставить в соответствие обратное - число, равное ему по модулю и имеющее противоположный знак. Следовательно, рассматриваемое множество является группой. Это дискретная абелева группа бесконечного порядка. Она имеет бесконечное количество подгрупп.

55

Так, например, подмножество четных чисел образует подгруппу, в чем легко убедиться непосредственной проверкой.

Пример 2. Рассмотрим множество, состоящее из четырех матриц:

В качестве операции умножения возьмем операцию умножения матриц. Для доказательства того, что это множество является группой, построим «таблицу умножения» (квадрат Кэли) этого множества:

замкнуто относительно операции умножения матриц. Умножение матриц, как известно, ассоциативно: в качестве единицы служит единичная матрица е , для

имеет нетривиальную подгруппу второго порядка, состоящую из элементов b и е . Квадрат Кэли для этой подгруппы имеет вид

be

b e b

e b e

Пример 3. Рассмотрим множество, состоящее из преобразований поворота пространства вокруг некоторой прямой на углы 90 ° , 180 ° , 270 ° и 360 ° .

В качестве операции «умножения» выберем последовательное выполнение поворотов, причем результатом «умножения» двух поворотов будет поворот вокруг той же оси на угол, равный сумме углов поворотов сомножителей по модулю

56

360 ° . Это значит, что если результирующий угол получится более 360 ° , то угол принимается равным −360 ° . Обозначая операцию поворота значением угла поворота, составим таблицу «умножения» для данного множества:

Нетрудно видеть, что данное множество также образует группу четвертого

совпадает с обратным. Эта группа содержит нетривиальную подгруппу второго

Заметим, что рассмотренные нами группы матриц и поворотов в примерах 2 и 3 различаются лишь обозначением элементов группового множества и конкретным смыслом, вкладываемым в понятие операции «умножения». Математические свойства этих групп полностью идентичны. В этом смысле группы неразличимы и называются изоморфными. При этом говорят, что одна из групп является изоморфным представлением другой. В общем случае

изоморфизм двух групп G и Н означает, что между элементами групповых множеств имеет место взаимно-однозначное соответствие, т. е. если элементам

Изоморфные друг другу группы с точки зрения теории групп являются конкретными реализациями одной и той же группы, элементы которой не имеют конкретного геометрического смысла. Такие группы называются абстрактными. Свойства, установленные для абстрактной группы, справедливы для всех изоморфных ей конкретных групп.

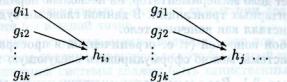
Между двумя группами G и Н может существовать и более общее соответствие, называемое гомоморфизмом. Пусть порядок группы G больше, чем порядок группы Н . Тогда одному и тому же элементу hi группы Н

57

могут быть сопоставлены сразу несколько элементов gi1 , gi2 ,... группы G . Схематически это можно представить следующим образом:

При этом произведение любых элементов gim g jm отображается в

произведение элементов hi h j .

Описывать (обозначать) группы можно несколькими способами. Для конечных групп небольшого порядка можно перечислить все элементы группового множества, указать операцию группового «умножения» и построить ее таблицу умножения. Однако для бесконечных групп и конечных групп достаточно большого порядка этот способ неприемлем.

Среди элементов группового множества всегда можно выделить конечное подмножество (в общем случае не являющееся подгруппой), такое, что при перемножении его элементов можно получить все остальные элементы группы. Такое подмножество называется множеством генераторов или образующих данной группы. Группы, обладающие одним генератором, называются циклическими. В циклических группах все элементы представляют собой «степени» одного генератора. Иначе говоря, все элементы циклической группы могут быть получены многократным перемножением ее генератора на себя. Нетрудно доказать, что циклическая группа обязательно является абелевой. Группы, приведенные в примерах 2 и 3, являются конечными циклическими.

Каждый элемент группы gi является генератором некоторой циклической подгруппы. Порядок этой циклической подгруппы называется порядком элемента группы gi .

Кроме отмеченных двух способов описания (обозначения) групп широко используется обозначение групп с помощью специальных символов.

58

Лекция 8

Точечные группы симметрии

Совокупность всех преобразований симметрии данного тела называют его группой преобразований симметрии или просто группой симметрии. Преобразования, входящие в состав группы симметрии тела конечных размеров (в частности, молекулы), должны быть такими, чтобы по крайней мере одна точка тела оставалась неподвижной при применении любого из этих преобразований. Другими словами, все оси и плоскости симметрии молекулы должны иметь по крайней мере одну общую точку пересечения. Действительно, последовательный поворот тела вокруг двух непересекающихся осей или отражение в непересекающихся плоскостях приводит к поступательному перемещению тела, которое, очевидно, не может совместить его с самим собой. Группы симметрии, обладающие указанным свойством, называются точечными группами.

Перед тем как перейти к построению возможных типов точечных групп, изложим простой геометрический способ, позволяющий легко произвести

распределение элементов группы по классам. Пусть Оа есть некоторая ось, а элемент группы А есть поворот вокруг этой оси на определенный угол. Пусть,

Поскольку А и В относятся к одному классу, то порядок этих элементов

одинаков; это значит, что они производят поворот на одинаковый угол.

Таким образом, мы приходим к результату, что два поворота на одинаковый угол относятся к одному классу, если в числе элементов группы имеется преобразование, с помощью которого можно совместить одну ось поворота с другой. Точно таким же образом можно показать, что и два отражения в различных плоскостях относятся к одному классу, если какое-либо преобразование группы переводит одну плоскость в другую. О самих осях или плоскостях симметрии, направления которых могут быть совмещены друг с другом, говорят как об эквивалентных.

59

Некоторые дополнительные замечания требуются для случая, когда оба поворота производятся вокруг одной и той же оси. Элементом, обратным

перпендикулярной оси (такой поворот меняет направление рассматриваемой оси на противоположное), то, согласно доказанному общему правилу, повороты

С kn и C−n k будут относиться к одному классу. Отражение m , в плоскости,

перпендикулярной к оси, тоже меняет ее направление на обратное; однако надо иметь в виду, что отражение меняет также и направление вращения. Поэтому

наличие m h не сделает элементы С kn и C−n k сопряженными. Отражение же m v в плоскости, проходящей через ось, не меняет направления оси, но меняет

вокруг оси на, одинаковый угол в противоположных направлениях сопряжены, то мы будем называть ось двухсторонней.

Определение классов точечной группы часто облегчается следующим

составляет сама по себе класс.

Перейдем теперь к перечислению всех возможных точечных групп. Мы будем строить их, начиная от простейших и прибавляя к ним новые элементы симметрии. Точечные группы будем обозначать жирными латинскими буквами с соответствующими индексами.

I. Группы C n

Простейший тип симметрии содержит всего одну ось симметрии n -ого порядка. Группа C n есть группа поворотов вокруг оси n -ого порядка. Эта

60

группа, очевидно, циклическая. Каждый из ее n элементов составляет сам по себе класс. Группа C 1 содержит только тождественное преобразование e и соответствует отсутствию какой бы то ни было симметрии.

II. Группы S2n

Это - группа поворотов вокруг зеркально-поворотной оси четного порядка 2n . Она содержит 2n элементов и является цикличесой. В частности, группа

). Все элементы группы коммутативны, т. е. группа абелева; число классов равно

IV. Группы C nv

Если присоединить к оси симметрии n -ого порядка проходящую через нее плоскость симметрии, то это автоматически приведет к появлению еще n−1

плоскостях. На рис. 8.1 изображены в качестве примера системы осей и плоскостей симметрии групп C 3v и C 4v .

Для определения классов замечаем, что благодаря наличию проходящих через ось симметрии плоскостей симметрии эта ось двусторонняя. Фактическое

распределение элементов по классам различно при четных и нечетных n .