Роботы

2.3.4. Преобразования систем координат для кинематической структуры манипулятора ПР

Координаты точки А в собственной системе координат звена 4 из-за наличия эксцентриситета в общем виде принимают значения: А9 (R9 cosα9, R9 sinα9, L9) (рис.2.5). Здесь величина L9 характеризует длину звена 9, а величина R9 - эксцентриситет точки А относительно оси вращения. Для вычисления координат этой же точки, но в системе 0 необходимо найти законы перехода между соседними системами координат, начиная с системы 9 и заканчивая системой 0.

Поскольку переходов, а следовательно, и матриц преобразования довольно значительное количество, то имеет смысл для сокращения математических выкладок функциональное описание расширенных матриц перехода (табл. 2.3).

Переход от 9й системы координат к 8й (рис. 2.18, а). Очевидно, что оси z9 и z8

взаимоперпендикулярны и в то же время оси x9 и z8 сонаправлены при любых значениях обобщенной координаты α8 во вращательной кинематической паре. Однако та же самая координата влияет на взаимную ориентацию осей у9 и y8. В данном случае имеет место сложный поворот осей, который мы делим на два простых: во-первых учитываем поворот вокруг оси z8 с тем, чтобы добиться сонаправленности осей у, а затем учетом поворота вокруг оси у добиваемся сонаправленности всех одноименных координатных осей.

Таблица 2.3. Функциональное описание расширенных матриц преобразования координат

Кроме вышеуказанного, необходимо учесть линейное смещение точек начал систем координат. Для этого достаточно определить координаты точки В, являющейся началом системы 9, в системе 8. Зависимости для их определения несложны и для выбранных направлений координатных осей в общем случае справедливо следующее выражение: B(L8cos(α8), L8sin(α8),0). Таким образом, для учета линейных смещений будет использоваться следующая матрица:

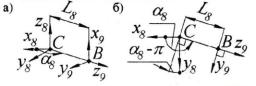
Рис. 2.18. Переход от системы 9 к системе 8.

Угловое смещение, обусловленное наличием обобщенной координаты α8, учитываем матрицей поворота вокруг оси z. Величина углового смещения в данном

случае равна ( y8 , y9 ) 8 (рис. 2.18, б), следовательно, матрица преобразования примет вид:

После сонаправления осей у обеих систем координат добиться сонаправленности остальных пар координатных векторов, не потеряв достигнутого результата, можно только поворотом вокруг оси у. После учета первого углового смещения как бы получается ситуация, изображенная на рис. 2.5. Учитываем угловое смещение с помощью матрицы поворота вокруг оси. Модуль углового смещения равен 90°, а его направление, определяемое знаком, - по часовой стрелке, если смотреть с положительного направления оси у. Следовательно, для правосторонней системы координат это отрица-

42

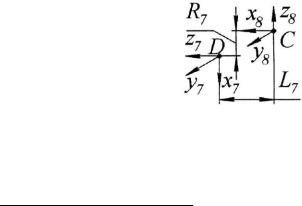
тельное направление. Значит, в матрицу поворота необходимо вместо общего значения угла поворота подставить значение -90°.

Таким образом, переход от системы координат 9 к системе 8, учитывающий все вышеприведенные действия, описывается некоторой матрицей4, которая получается в результате перемножения матриц, учитывающих каждое из оговоренных элементарных действий:

M9 8 M M ' M '' Ms(L8 cos( 8 ), L8 sin( 8 ),0) M z ( 8 ) M y ( / 2).

Перейдем теперь к преобразованию системы координат 8 к системе 7 (рис. 2.19). Обе эти системы ориентированы друг относительно друга постоянным образом, поскольку вращения в кинематической паре 7 не происходит. Также остаются постоянными и величины лилейных смещений точек начал систем координат, поскольку при назначении собственных систем координат для данной кинематической структуры согласно п. 2.2.4 учет линейного перемещения s7 в паре 7 происходит в системе координат 6.

Величины и направления линейных смещений исчерпывающим образом описываются координатами точки С в системе 7: С(-R7,0,-L7). Это означает, что матрица преобразования будет иметь вид: М=Мs(-R7,0,-L7).

Рис. 2.19. Переход от системы 8 к системе 7.

Угловое смещение координатных векторов относительно одноименных им, хотя и постоянное, но имеется. В частности из трех пар координатных векторов со-

4 Здесь и далее матрицы преобразований в целях сокращения видимого объема пояснений в виде таблицы элементов представляться не будут.

43

Для учета этой ситуации необходимо воспользоваться матрицей поворота вокруг оси у на угол -π/2, т.е. M ' M y ( / 2).

Окончательный вид матрицы перехода от системы 8 к системе 7:

M8 7 M M ' Ms( R7 ,0, L7 ) M y ( / 2).

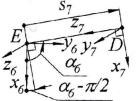
Далее предстоит найти матрицу преобразования координат точек из системы 7 в систему 6 (рис. 2.20). При этом необходимо отметить, что независимо от значений обобщенных координат α6 и s7 координатные вектора z6 и y7 остаются сонаправленными, а, например, пара векторов z в силу конструктивных особенностей манипулятора всегда взаимоперпендикулярна.

Рис.2.20. Переход от системы 7 к системе 6 На величину линейных смещений оказывает влияние не только координата

α6, но и s7, поскольку точка D, являющаяся началом системы 7 в 6й системе имеет следующие координаты: D (s7·cos (α6), s7·sin (α6), 0). Это означает, что для учета линейных смещений между системами необходимо использовать матрицу вида:

M Ms(s7 cos( 6 ), s7 sin( 6 ),0).

Для учета углового смещения, создаваемого обобщенной координатой α6 во вращательной кинематической паре, необходимо использовать матрицу поворота вокруг оси z. Исходя из взаимного расположения координатных векторов, заметим,

угол α6-π/2 вокруг оси z, сонаправив тем самым оси х. Однако остальные одноименные координатные вектора будут смещены вокруг оси х на угол 90°, что математически выльется в использование матрицы M '' M x ( / 2).

Матрица полного перехода между этими системами имеет вид

M7 6 M M ' M '' Ms(s7 cos( 6 ), s7 sin( 6 ),0) M z ( 6 / 2) M x ( / 2).

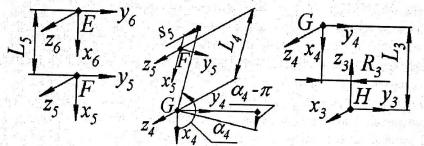
При переходе от системы координат 6 к 5й системе (рис. 2.21) для рассматриваемой кинематической структуры расположение точек начал относительно друг друга постоянно и описывается следующими координатами Е(-L5,0,0). Кинематическая пара 5 не вращательного действия, что в совокупности с фактом изначальной попарной

44

сонаправленности координатных векторов, исключает необходимость учета углового смещения систем координат. Следовательно, матрица перехода будет иметь вид:

M6 5 Ms( L5 ,0,0).

В свою очередь система 5 имеет как линейное, так и угловое смещения относительно системы 4 (рис. 2.22). Оба смещения переменны и находятся в зависимости от обобщенных координат α4 и s5. На величину линейного смещения вдоль осей х4 и у4 влияет обобщенная координата α4 и постоянный параметр L4 (длина звена 4), а вдоль оси Z4-S5. Окончательно имеем координаты точки начала системы 5 в системе 4: F(L4 cos( 4 ), L4 sin( 4 ), s5 ) ; и матрицу учета линейных смеще-

ний: M Ms(L4 cos( 4 ), L4 sin( 4 ), s5 ).

Характер углового смещения для данного перехода аналогичен ситуации, сложившейся при конвертации координат системы 7 в координаты системы 6, т.е.

Учитывая все приведенные данные, касающиеся перехода от 5й системы к 4й, получаем следующую матрицу перехода

M5 4 M M ' Ms(L4 cos( 4 ), L4 sin( 4 ), s5 ) M z ( 4 ).

Система 4, жестко связанная со звеном 3, имеет линейные смещения вдоль осей y3 и z3 , обусловленные конфигурацией и размерами звена 3 (рис. 2.23). Последнее находит свое отражение в координатах точки G(0,-R3,L3). Что касается угловых смещений, то из всех координатных векторов обеих систем сонаправлены только оси у, поэтому требуется учесть угловое смещение относительно указанной оси на величину 90°. Окончательно получаем вид матрицы перехода между системами

45

M4 3 Ms(0, R3 , L3 ) M y ( / 2).

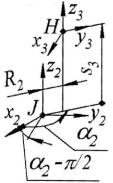
Описывая переход от системы 3 к системе 2 (рис. 2.24) можно заметить, что ротация в кинематической паре 2 звена 2 при сохранении сонаправленности осей z обеих систем, приводит к появлению углового смещения в остальных парах координатных векторов, что необходимо учесть с помощью матрицы поворота вокруг оси z. Задача составления матрицы перехода в этом случае аналогична решенной при конвертации координат системы 5 в координаты системы 6. Однако в данном случае значение углового смещения вокруг оси z равно α2-π/2.

Рис.2.24. Переход от системы 3 к системе 2

Рассматривая линейные смещения, необходимо отметить, что конфигурация звена 2 манипулятора (а именно размер R2) и обобщенные координаты s3 и α2 безусловно оказывают влияние на значение этих смещений. Последнее наглядно можно продемонстрировать на координатах точки Н в общем виде в системе 2: H(R2 cos(α2),R2 sin(α2),s3). Итоговая матрица перехода между системами координат имеет вид:

M3 2 Ms(R2 cos( 2 ), R2 sin( 2 ), s3 ) M z ( 2 / 2).

При конвертации координат системы 2 в систему 1 (рис. 2.25) необходимо, как и во всех предыдущих случаях, учесть как линейные, так и угловые смещения системы, которую приводят, относительно системы, к которой приводят. Система 2, жестко связана со звеном 1 (как впрочем, в данном случае и система 1), которое имеет возможность поступательного перемещения в кинематической паре. Необходимо отметить, что при этом относительном движении линейные смещения точек начал систем координат остаются постоянными - на величину Li (длину звена 1) вдоль оси х, что находит свое отражение в координатах точки J: J(L1, 0,0). Следовательно, матрица учета этого смещения в функциональной форме запишется следующим образом: М = Ms (-L1, 0,0).

46

Рис. 2.25. Переход от системы 2 к системе 1.

Из трех пар одноименных осей постоянно сонаправлены только у, остальные же имеют фиксированное угловое смещение на угол -90°. Последнее находит свое отражение в использовании матрицы перехода вида: М'=Mφy(-π/2).

Итоговое преобразование указанных систем координат осуществляется с помощью матрицы:

M 2 1 M M ' Ms( L1,0,0) M y ( / 2).

И, наконец, последнюю конвертацию необходимо осуществить между системами 1 и 0 (рис. 2.26). Здесь, как и в предыдущем случае, взаимная ориентация осей систем координат имеет фиксированное угловое смещение, однако теперь линейное смещение переменно и зависит от обобщенной координаты s1.

Величины линейных перемещений выявляются уже традиционным способом - нахождением координат точки начала последующей системы относительно предыдущей. При данном направлении осей системы 0 координаты точки начала системы 1 имеют вид: К (s1,0,0). Это приводит к необходимости использования матрицу линейного сдвига: М =Ms(sl,0,0).

Рис.2.26. Переход от системы 1 к системе 0 Угловое смещение происходит вокруг оси у на угол 90°, что находит свое от-

ражение в применении следующей матрицы: М' = Мφу (π/2).

Таким образом, полный переход от координат системы 1 к координатам системы 0 производится с помощью матрицы:

M1 0 M M ' Ms(s1,0,0) M y ( / 2).

Получив матрицы перехода между соседними системами, имеем матрицу пре-

47

образования координат в собственной системе схвата манипулятора к координатам в неподвижной системе, связанной со стойкой робота:

M9 0 M1 0 M2 1 M3 2 M4 3 M5 4 M6 5 M7 6 M8 7 M9 8.

Конечное выражение преобразования координат точки схвата манипулятора к системе стойки робота имеет вид:

А0 M1 0 А9

Компьютерная реализация данного алгоритма и получение вектора, содержащего координаты точки схвата робота относительно его стойки в численном виде, являются решением поставленной прямой задачи о положениях пространственного манипулятора.

Частные вопросы, касающиеся компьютерной реализации алгоритма в среде MathCAD, приведены далее.

3.Реализация вычислительного алгоритма на ЭВМ

Врамках данного раздела будет рассматриваться использование компьютерной техники при решении поставленной прямой задачи о положениях. Работа, проделанная в предыдущем разделе, позволила определить необходимые действия для получения решения. Причем сам алгоритм обладает определенной универсальностью, поскольку все преобразования для конкретного вида кинематической

структуры проведены в общем виде, что при реализации на ЭВМ дает возможность при численном изменении как постоянных (размеров звеньев), так и переменных (обобщенных координат) параметров структуры получать численный ответ.

3.1. Работа с системой MathCAD

Обзор возможностей системы в рамках данного пункта будет производиться на основе версии MathCAD 2001 Professional, работающей в рамках операционных систем класса Windows, однако описанные приемы работы во многом справедливы как для более ранних версий (MathCAD 2000, 8 и т.д.), так и для более поздних версий MathCAD. Объем сведений, приведенные ниже, не описывает систему исчерпывающим образом, однако достаточен для реализации алгоритма решения прямой задачи о положениях.

3.1.1. Общее описание системы и ее запуск

MathCAD – это система компьютерной математики. Сочетание удобного и простого интерфейса системы с довольно гибкими и производительными вычислительными возможностями делает эту среду одной из самых оптимальных для реализации вычислительных алгоритмов средней сложности.

48

Для запуска среды MathCAD имеется несколько вариантов:

– с помощью ярлыка на рабочем столе Windows;

–с помощью ярлыка на панели быстрого запуска Windows;

–через меню «Пуск»: Пуск ► Программы ► Mathsoft Apps ► Mathca Professional (этот путь задается при установке по умолчанию);

–запустить файл C: \ Program Files \ MathSoft \ Mathcad Professional \

math-cad.exe (этот путь задается при установке по умолчанию);

–запустить любой файл с расширением .mcd.

При недостатке или отсутствии опыта работы на ЭВМ лучше обратиться к более опытным пользователям или администратору компьютера.

3.1.2. Общие приемы работы в среде

Прежде всего необходимо отметить, что скорость и удобство работы со средой MathCAD 2001 Pro зависят в конечном счете от самого пользователя: будет ли он активно применять графический интерфейс среды, либо ограничится определенными сочетаниями клавиш (так называемыми «горячими» клавишами). Обычно начинающим проще работать с графическим интерфейсом, и как следствие, с пиктограммами команд. Поэтому необходимо позаботиться о присутствии на экране панелей с нужными пиктограммами с помощью меню View ► Toolbars. Следует отметить, что все пункты этого меню ниже строки Math можно в дальнейшем вызы-

вать с помощью пиктограмм панели Math

Панели можно располагать в произвольном месте рабочей области, перетаскивая их с помощью мыши (нажав и удерживая кнопку команды), либо «приклеивать» панели к краям экрана.

Работа в среде происходит в пределах рабочего пространства – worksheet. Алгоритм реализуется с помощью различных блоков присваивания, а результат выводится на экран с помощью блоков визуализации. По умолчанию фон рабочего поля – белый и границы блоков не видны. Чтобы отчетливо видеть эти границы необходимо задать команду с помощью меню View ► Regions.

Точка, с позиции которой будет осуществляться ввод нового блока, обозначается с помощью символа «+» (красного перекрестья). Влиять на положение этого символа можно с помощью клавиш управления курсором или же с помощью «мыши» указать нужную точку и нажать на клавишу команды (левую при настройке для правши и правую – для левши).

Всреде существуют инструменты, позволяющие облегчить задачу оформления документа. Вертикальные и горизонтальные линии на рабочем поле делят его на страницы, формат, ориентация и поля которых устанавливаются с помощью ме-

ню File ► Page Setup…

Впроцессе работы блоки могут накладываться один на другой, что портит

49

оформление и затрудняет видимость блоков. Для устранения этого необходимо с помощью мыши подвести указатель к границе блока, и когда указатель примет форму ладошки, нажав и удерживая кнопку команды, перетащить блок в другое место. Для автоматического разделения блоков существует команда меню Format ► Separate Regions.

Кроме этого, для выравнивания блоков необходимо воспользоваться соответствующими командами с помощью пиктограмм панели View ► Toolbars ► Stan-

dard:– выравнивание по горизонтали;– выравнивание по вертикали. Эти же команды доступны с помощью меню: Format ► Align Regions ►Across (Down). Данные операции могут понадобиться не только для красоты оформления, но и, например, в следующем случае: блок вывода результата визуально находится после блока выполнения действий (присваивания), однако система MathCAD не отображает результат и, вдобавок, выводит сообщение об ошибке. Дело в том, что выполнение действий происходит последовательно – сверху вниз и слева направо. Это означает, что активные блоки операций выполняются в указанной последовательности, причем позиции блоков строго контролируются системой MathCAD и выравнивание блоков «на глазок» не всегда приводит к правильному результату, поэтому логичнее воспользоваться придумкой разработчиков системы.

Здесь было указано, что исполняются только активные блоки, в то время как неактивные игнорируются системой. По умолчанию все блоки активны, однако при отладке программы может потребоваться деактивация. О неактивности блока говорит небольшой черный прямоугольник «■» в правом верхнем углу блока. Деактивировать блок можно с помощью его меню, щелкнув на блоке «мышиной» клавишей меню, выбрать пункт Disable Evaluation или нажать клавишу «d» при высвеченном меню. Для активации блока указанные действия остаются справедливыми с той лишь разницей, что пункт меню будет называться Enable Evaluation, а клавиша будет «e».

В некоторой степени задачу оформления документа может облегчить отображение линейки, которая вызывается с помощью меню View ► Ruler.

Кроме этого, следует упомянуть о еще одном эффективном средстве, позволяющем сделать структуру алгоритма более наглядной. Этим средством являются области, которые вставляются в документ с помощью меню Insert ► Area5. Визуально область ограничивается двумя горизонтальными линиями, вставка и удаление которых происходит только парами. По умолчанию верхняя линия начинается с символа «▼», а нижняя - с символа «▲». Удобство работы с использованием областей заключается в том, что при двойном щелчке на какой-либо из линий область «схлопывается» в одну линию, начинающуюся с символа «►», и прячет блоки, ра-

5 В MathCAD 11 вставку можно осуществить с помощью контекстного меню на свободном пространстве рабочего листа.

50