Роботы

правлением нормали к последней указанной плоскости.

В этой системе для данной кинематической структуры не происходит учета каких-либо перемещений, обусловленных изменением обобщенных координат, однако ее удобно использовать для описания линейных смещений точки С вращательной кинематической пары 8, вызванных наличием постоянных параметров структуры – размерами и топологией звеньев.

Система 8 служит для описания поворота звена 8 относительно звена 7, обеспечиваемого изменением значения обобщенной координаты α8 во вращательной кинематической паре 8, соединяющей указанные звенья. Начало этой системы находится в точке С (рис.2.5). Ось z8 направлена вдоль оси вращения, ось х8 совмещена с линией звена 7 и исходит из точки С, ось у8 перпендикулярна плоскости звена и дополняет правую тройку координатных векторов. В этом случае также удалось сонаправить оси у систем 7 и 8.

Угол α8, отсчитываемый от положительного направления оси х8 (т.е. фактически от осевой линии звена 7), фиксирует осевую линию звена 8. Другими словами, угол α8 заключен между двумя звеньями.

Система 9 является собственной для звена 9, относительно которой описывается ротация схвата. Ось z9 совпадает с осью ротации, ось х9 параллельна оси z8, а направление оси у9 делает данную систему координат правосторонней. Следует отметить, что при α8 =180o оси у систем 8 и 9 будут сонаправлены (рис. 2.5).

Обобщенная координата α9, описывающая ротацию звена 9, отсчитывается от положительного направления оси х9 и фиксирует плоскость звена 9. В частности на рис. 2.5 изображен случай, когда α9 = 0o .

Подытоживая результаты этого этапа решения прямой задачи о положениях, необходимо отметить, что в том положении кинематической структуры, которое изображено на рис. 2.5, на нас направлены следующие оси: х0, z1, х2, х3, z4, z5, z6, y7, y8, y9. На эскизе порядок их изображения следующий: выбирается направление под произвольным углом и принимается, что в этом направлении будут откладываться координатные вектора, перпендикулярные плоскости листа. Причем, если вектора направлены на нас, то рекомендуется ориентировать их вдоль выбранного направления смотрящими вниз, в то время как направленные от нас – смотрящими вверх. Например, на рис. 2.5 указанные выше вектора параллельны друг другу при любой взаимной ориентации звеньев структуры и смотрят в левый нижний угол, в то время как идущие от нас вектора, сохраняя параллельность смотрели бы в верхний правый угол листа.

21

2.3.Преобразования систем координат

2.3.1.Общие принципы преобразования систем координат

Пусть в пространстве введены две общие декартовы системы координат xyz и х'у'z' (рис.2.6.). Выразим координаты произвольной точки А в системе координат x'y'z' через координаты ее в системе xyz.

Рис. 2.6. Преобразование двух общих декартовых систем координат Имеем

Выражения в скобках в этой формуле суть координаты вектора О' A относительно

В векторно-матричной форме:

(2.2)

Если обе системы координат x, y, z и x' , y' , z' прямоугольные, то коэффициенты формул удовлетворяют условиям ортогональности

Очевидно, что для перехода от системы координат x' , y' , z' к системе x'' , y'' , z'' будет использоваться следующее выражение:

Тогда для перехода от системы x, y, z к системе x'' , y'' , z'' справедливо следующее выражение:

Следует отметить, что выше изложен метод преобразования декартовых систем координат в общем случае. Его достоинство проявляется в получении единственной матрицы перехода между двумя системами и вектора, содержащего координаты точки начала приводимой системы. Этот метод приводит к верным результатам, но довольно громоздок и потому не слишком удобен при решении прямых задач о положениях. Так, например, он трижды требует решения задачи о представлении координатных векторов старой системы в базисе координатных векторов но-

23

вой системы. Следствием этого является увеличение объема вычислительных операций вспомогательного характера и размывание конечной цели расчета.

С увеличением числа конвертируемых систем векторно-матричное уравнение перехода от первой системы к последней усложняется. Кроме этого, в конечном выражении преобразования координат используются матрица и вектор, что нарушает единообразие операций. Это несколько усложняет конструирование вычислительного алгоритма для ЭВМ. Применение механизма рекурсии при росте количества координатных систем также является неоправданным с точки зрения затрачиваемых ресурсов.

В робототехнике (и других областях науки) при решении задач конвертирования декартовых систем координат используется несколько иной подход. Основываясь на особенности исполнительных механизмов ПР, описанной во введении, а именно, что оси соседних кинематических пар или параллельны, или перпендикулярны между собой, можно существенно упростить решение прямой задачи о положениях, назначая ортогональные декартовы системы координат.

Кроме этого, при конвертации применяются расширенные матрицы перехода,

матрица перехода. Введем в рассмотрение матрицу 4х4 следующей архитектуры:

Или в развернутом виде

Матрица М носит название расширенной матрицы перехода

Модифицировав векторы v и v' следующим образом: ' x' , y' , z' ,1 T ,

x, y, z,1 T , получим уравнение, так же описывающее переход от одной системы координат к другой:

24

Для описания перехода от системы координат хуz к системе x'' , y'' , z'' через систему х'y'z' справедливо выражение:

При наличии n систем координат переход от системы n к системе 1 будет выглядеть так:

n

1 M1 2 M2 3 Mn 1 n 2 Mn n 1 n или 1 Mi i 1 n

i 1

Произвольной ориентации твердого тела и жестко связанной с ним системы координат можно добиться с помощью независимых (либо зависимых) друг от друга вращательных и/или поступательных смещений относительно трех осей неподвижной системы координат, что реализует принцип степеней свобод, описанный в п. 1.1.

Каждое из смещений математически описывается с помощью специальной матрицы перехода. Всего таких матриц шесть: по одной на каждую из степеней свободы. Рассмотрим далее принципы получения этих матриц.

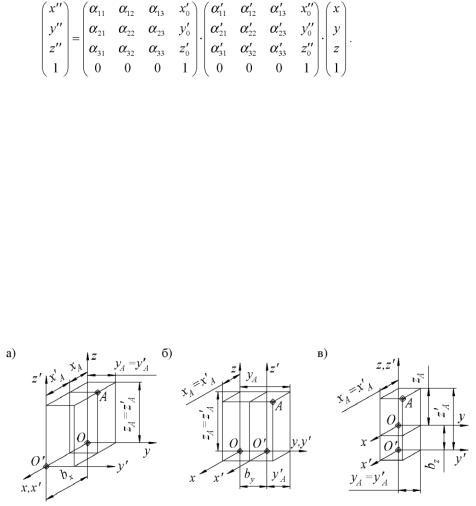
Начнем со случаев математического описания поступательного смещения вдоль какой-либо из координатных осей. Пусть в пространстве введены две ортогональные декартовы системы координат xyz и х'у'z' с точками начал О и О' соответственно, причем одноименные оси обеих систем сонаправлены, а точка О' смещена относительно точки О на величину bx вдоль оси Ох (рис. 2.7 а).

Рис. 2.7. Линейные смещения систем координат относительно друг друга: а – вдоль оси х; б – вдоль оси у; в – вдоль оси z.

Для всех трех рассматриваемых случаев на основании сонаправленности одноименных координатных векторов имеем следующее представление векторов

25

3) Для случая смещения точек начал двух систем вдоль оси Оz на расстояние bz (рис.2.7 в) имеется следующее векторно-матричное уравнение:

Расширенные матрицы перехода для рассмотренных случаев приведены в табл. 2.1.

Таблица 2.1 Расширенные матрицы преобразования координат

для учета линейных смещений

Следует отметить, что они коммутируют между собой, а также любая из этих матриц коммутирует с матрицей, полученной при перемножении двух других. Это математическое свойство находит подтверждение и при анализе действий, описываемых матрицами. Ведь если объект необходимо доставить в точку с координатами (x,y,z), то не важна очередность перемещения объекта вдоль координатных осей, чтобы доставить его в заданную точку. Таким образом, можно использовать вместо трех одну универсальную матрицу, учитывающую линейные смещения приводимой системы относительно той, к которой приводят:

где величины bx, by, bz по существу является координатами точки начала приводимой системы координат в системе координат, к которой приводят (далее это

27

будет рассмотрено на конкретных примерах).

Теперь перейдем к математическому описанию углового смещения вокруг какой-либо из координатных осей. Пусть в пространстве введены две ортогональные декартовы системы координат xyz и x’y'z' с совпадающими точками начал О и О' соответственно. При этом система xyz повернута на некоторый угол

α:

1)вокруг оси Ох (рис. 2.8, а);

2)вокруг оси Оу (рис. 2.9, а);

3)вокруг оси Oz (рис. 2.10, а).

Выразим координаты произвольной точки А в системе координат x'y'z' через координаты ее в системе xyz.

Для всех трех рассматриваемых случаев в силу совпадения точек начал систем координат имеем:

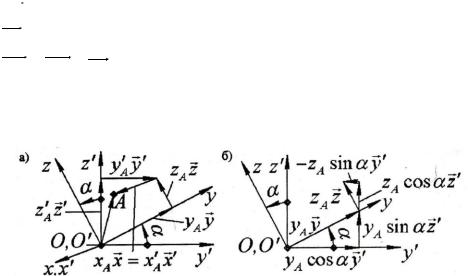
1) при повороте вокруг оси Ох (рис.2.8, б):

Рис.2.8 Угловые смещения систем координат относительно друг друга вокруг оси х: а- векторное представление координат точки; б - преобразование векторов.

28

2) при повороте вокруг оси Оу (рис.2.9, б):

Рис. 2.9. угловые смещения систем координат относительно друг друга вокруг оси y: а – векторное представление координат точки; б – преобразование векторов.

29

3) при повороте вокруг оси Оz (рис.2.10, б):

Рис. 2.10. Угловые смещения систем координат относительно друг друга вокруг оси z: a- векторное представление координат точки; б – преобразование векторов.

Подставляя полученные зависимости в выражение, получим

Расширенные матрицы перехода приведены в табл. 2.2.

Таблица 2.2 Расширенные матрицы преобразования координат для учета

угловых смещений

Таким образом, в табл. 2.1 и 2.2 приведены шесть матриц преобразования, которые реализуют принцип шести степеней свободы. Следует отметить, что матрицы угловых смещений в общем случае между собой не коммутируют, однако они коммутируют с матрицами линейных смещений. Отвлекаясь от математики, вышеска-

30