
- •Конспект лекций.
- •1.1.2.Закон кулона
- •1.1.3.Электрическое поле. Напряженность
- •1.1.4.Принцип суперпозиции электрических полей
- •1.1.5. Примеры расчета полей на основе
- •Лекция 3
- •1.1.6. Густота линий напряженности. Поток вектора напряженности
- •1.1.7. Теорема гаусса
- •1.1.8.Применение теоремы гаусса к расчету полей
- •1.1.9.Потенциальный характер электростатического поля.Работа сил поля при перемещении зарядов. Циркуляция и ротор вектора напряженности
- •1.1.10.Потенциал. Потенциальная энергия заряда в электростатическом поле
- •1.1.11.Связь между напряженностью и потенциалом
- •1.1.12. Уравнение пуассона
- •1.1.13. Эквипотенциальные поверхности
- •Лекция 5
- •1.2. Электрическое поле в диэлектриках
- •1.2.1.Полярные и неполярные молекулы
- •1.2.2. Диполь в однородном и неоднородном электрических полях
- •1.2.3Поляризация диэлектриков
- •1.2.4. Поле внутри диэлектрика. Свободные и связанные заряды
- •1.2.5. Вектор электрического смещения
- •1.2.8.Условия на границе двух диэлектриков
- •1.2.7. Примеры расчета электрических полей в диэлектриках
- •1.3.Проводники в электрическом поле
- •1.3.1.Распределение зарядов на проводнике
- •1.3.2.Проводник во внешнем электрическом поле
- •1.3.3.Электроемкость уединенного проводника
- •1.3.4. Взаимная электроемкость. Конденсаторы
- •1.3.5. Соединения конденсаторов
- •1.4.Энергия электрического поля
- •1.4.1.Энергия заряженного проводника
- •1.4.2.Энергия заряженного конденсатора
- •1.4.3.Энергия поляризованного диэлектрика
- •1.4.4. Закон сохранения энергии для электрического поля в несегнетоэлектрической среде
1.1.8.Применение теоремы гаусса к расчету полей
Найдем напряженность электрического поля бесконечной нити, заряженной с линейной плотностью заряда
 (рис.1.1.10).
Построим гауссову поверхность в виде
ц
(рис.1.1.10).
Построим гауссову поверхность в виде
ц илиндра,
ось которого совпадает с нитью. Радиус
цилиндраr,
высота h
. В силу симметрии
рассматриваемого поля линии вектора
напряженности
илиндра,
ось которого совпадает с нитью. Радиус
цилиндраr,
высота h
. В силу симметрии
рассматриваемого поля линии вектора
напряженности
 расходятся радиально от нити, и поток
вектора
расходятся радиально от нити, и поток
вектора отличен от нуля только через боковую
поверхность цилиндра:
отличен от нуля только через боковую
поверхность цилиндра:
![]()
Очевидно, на одинаковом
расстоянии r
от нити значения Е
будут одинаковы, поэтому
![]() Согласно теореме Гаусса
Согласно теореме Гаусса
![]()
где
![]() -
заряд, заключенный внутри гауссова
цилиндра. Тогда
-
заряд, заключенный внутри гауссова
цилиндра. Тогда
![]()
и
![]() - напряженность поля заряженной нити
на расстоянииr
от нее.
- напряженность поля заряженной нити
на расстоянииr
от нее.
2 .
Поле бесконечной однородной заряженной
плоскости. Поверхностная плотность
заряда
.
Поле бесконечной однородной заряженной
плоскости. Поверхностная плотность
заряда![]() во всех точках плоскости одинакова
во всех точках плоскости одинакова![]() .
Напряженность поля перпендикулярна к
плоскости. В симметричных относительно
плоскости точках напряженность поля
одинакова по величине и противоположна
по направлению. Построим цилиндрическую
поверхность с образующими, перпендикулярными
к плоскости, и основаниями
.
Напряженность поля перпендикулярна к
плоскости. В симметричных относительно
плоскости точках напряженность поля
одинакова по величине и противоположна
по направлению. Построим цилиндрическую
поверхность с образующими, перпендикулярными
к плоскости, и основаниями![]() (рис.1.1.11). В силу симметрии
(рис.1.1.11). В силу симметрии![]() .
.
П оток
через боковую поверхность
равен нулю, так как вектор
оток
через боковую поверхность
равен нулю, так как вектор![]() перпендикулярен к этой поверхности,
таким образом суммарный поток через
поверхность цилиндра равен
перпендикулярен к этой поверхности,
таким образом суммарный поток через
поверхность цилиндра равен![]() ,
и
,
и![]() .
.
3.Рассмотрим электрическое
поле, созданное двумя разноименно
заряженными плоскостями с поверхностными
плотностями заряда
![]() и
и![]() .
Очевидно, напряженности полей плоскостей
направлены в одну сторону (от положительной
плоскости к отрицательной, рис.1.1.12), и
р
.
Очевидно, напряженности полей плоскостей
направлены в одну сторону (от положительной
плоскости к отрицательной, рис.1.1.12), и
р езультирующая
напряженность
езультирующая
напряженность![]() ,
где
,
где![]() - напряженность поля одной заряженной
плоскости. Окончательно получаем
- напряженность поля одной заряженной
плоскости. Окончательно получаем
![]()
4.Вычислим напряженность
электрического поля, создаваемого
заряженной сферой радиуса R.
Заряд сферы q,
его поверхностная плотность
![]() Для определения напряженности построим
гауссову поверхность в виде сферы
радиусаr,
центр которой совпадает с центром
заряженной сферы (рис.1.1.13).
Для определения напряженности построим
гауссову поверхность в виде сферы
радиусаr,
центр которой совпадает с центром
заряженной сферы (рис.1.1.13).
 Приr≤R
внутри гауссовой
поверхности зарядов нет, так как весь
заряд распределен по поверхности сферы.
По теореме Гаусса
Приr≤R
внутри гауссовой
поверхности зарядов нет, так как весь
заряд распределен по поверхности сферы.
По теореме Гаусса
![]() или
или![]() ,
следовательно,
,
следовательно,![]() - напряженность электрического поля
внутри заряженной сферы равна нулю.
- напряженность электрического поля
внутри заряженной сферы равна нулю.
 При
При
![]() внутрь гауссовой
поверхности попадает весь заряд q
сферы. В силу центральной симметрии
поля напряженность на расстоянии r
от центра сферы всюду одинакова, и
внутрь гауссовой
поверхности попадает весь заряд q
сферы. В силу центральной симметрии
поля напряженность на расстоянии r
от центра сферы всюду одинакова, и
![]() или
или![]() при этом
при этом![]() ,
тогда
,
тогда![]() ,
и
,
и![]() С ростомr
значения Е убывают
пропорционально
С ростомr
значения Е убывают
пропорционально
![]() (рис.1.1.14). На поверхности
сферы напряженность испытывает скачек
(рис.1.1.14). На поверхности
сферы напряженность испытывает скачек
![]()
5.Рассмотрим электрическое поле, созданное объемно заряженным шаром радиуса R . Объемная плотность заряда шара ρ. Гауссову поверхность построим в виде сферы, центр которой совпадает с центром шара, а радиус равен r (рис.1.1.15).
При
![]() внутрь гауссовой
поверхности попадает заряд
внутрь гауссовой
поверхности попадает заряд
![]() ,
тогда по теореме Гаусса
,
тогда по теореме Гаусса
![]() ,
и
,
и![]() .
На поверхности шара приr=R
напряженность
.
На поверхности шара приr=R
напряженность
![]() .
.
 При
При![]() внутрь гауссовой поверхности попадает
весь заряд
внутрь гауссовой поверхности попадает
весь заряд![]() ,
и
,
и![]() ,
отсюда
,
отсюда![]() На поверхности сферы
На поверхности сферы![]() т.е.
т.е.![]() и скачка напряженности не происходит.
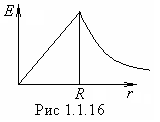
Зависимость
и скачка напряженности не происходит.
Зависимость![]() представлена на рис1.1.16.
представлена на рис1.1.16.
Лекция 4
1.1.9.Потенциальный характер электростатического поля.Работа сил поля при перемещении зарядов. Циркуляция и ротор вектора напряженности
Работа, совершаемая
силами электростатического поля при
перемещении заряда
![]() на отрезок
на отрезок![]() равна:
равна:
![]() .
.
Работа по перемещению единичного положительного заряда численно равна
![]()
Работа, совершаемая при
перемещении единичного положительного
заряда по конечному пути
![]() равна
равна
![]() .
(1.1.2)
.
(1.1.2)
Здесь
![]() - сила Кулона, которая является центральной
силой. Из механики известно, что поле
центральных сил консервативно.
Следовательно, работа электростатического
поля по перемещению заряда не зависит
от траектории, а определяется только
начальной и конечными ее точками. Работа
по замкнутому пути равна нулю. Поле,
обладающее такими свойствами, называется
потенциальным. Тогда из (1.1.2) имеем:
- сила Кулона, которая является центральной
силой. Из механики известно, что поле
центральных сил консервативно.
Следовательно, работа электростатического
поля по перемещению заряда не зависит
от траектории, а определяется только
начальной и конечными ее точками. Работа
по замкнутому пути равна нулю. Поле,
обладающее такими свойствами, называется
потенциальным. Тогда из (1.1.2) имеем:
![]() (1.1.3)
(1.1.3)
- циркуляция
вектора
![]() по замкнутому пути равна нулю.Поле,
обладающее такими свойствами, называется
потенциальным.
по замкнутому пути равна нулю.Поле,
обладающее такими свойствами, называется
потенциальным.
Докажем потенциальный характер электростатического поля.
 Рассмотрим
сначала работу электрических сил в поле
элементарного точечного заряда
Рассмотрим
сначала работу электрических сил в поле
элементарного точечного заряда![]() .
Работа этих сил при бесконечно малом
перемещении
.
Работа этих сил при бесконечно малом
перемещении![]() пробного единичного положительного
заряда равна:
пробного единичного положительного
заряда равна:
![]() ,
,![]()
где
![]() - проекция перемещения пробного заряда
- проекция перемещения пробного заряда![]() на радиус-вектор
на радиус-вектор![]() ,
проведенный из возбуждающего поле
заряда
,
проведенный из возбуждающего поле
заряда![]() .
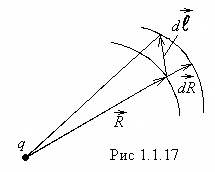
Из рис.1.1.17 видно, что
.
Из рис.1.1.17 видно, что![]() - это приращение
численного значения радиус-вектора
- это приращение
численного значения радиус-вектора![]() ,
то есть увеличение расстояния пробного
заряда
,
то есть увеличение расстояния пробного
заряда![]() от заряда
от заряда![]() .
Поэтому работа
.
Поэтому работа![]() может быть представлена как полный
дифференциал скалярной функции точки
может быть представлена как полный
дифференциал скалярной функции точки![]() :
:
![]() ,
,
где
![]() - численное значение радиус-вектора
- численное значение радиус-вектора![]() .
Тогда работа по перемещению единичного
положительного заряда из точки
.
Тогда работа по перемещению единичного
положительного заряда из точки![]() в точку
в точку![]() по конечному пути
по конечному пути![]() равна:
равна:
![]() ,
,
г де
де![]() и
и![]() - расстояния начальной и конечной точек
пути от заряда
- расстояния начальной и конечной точек
пути от заряда![]() .
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижного
.
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижного
элементарного точечного заряда
действительно зависит от положений
начальной и конечной точек этого пути
и не зависит от формы пути. На рис.1.1.18
работа на пути
![]() равна работе на пути
равна работе на пути![]() :
избыточная работа, совершаемая на пути
:
избыточная работа, совершаемая на пути![]() при перемещении пробного заряда за
пределы сферы радиуса
при перемещении пробного заряда за
пределы сферы радиуса![]() ,
компенсируется отрицательной работой,
совершаемой при последующем приближении
пробного заряда к заряду
,
компенсируется отрицательной работой,
совершаемой при последующем приближении
пробного заряда к заряду![]() на последнем участке пути
на последнем участке пути![]() .
Таким образом, поле неподвижного
точечного заряда есть поле потенциальное.
.
Таким образом, поле неподвижного
точечного заряда есть поле потенциальное.
Очевидно, сумма потенциальных полей тоже есть потенциальное поле (так как если работа слагаемых сил не зависит от формы пути, то и работа равнодействующей от нее не зависит). Поле произвольной системы зарядов можно рассматривать как сумму полей каждого из точечных зарядов, поэтому всякое электростатическое поле есть поле потенциальное.
По определению, проекция
![]() на произвольное направление поля
на произвольное направление поля![]() равна
равна
![]() ,
,
где
![]() - бесконечно малая площадка, проходящая
через точку
- бесконечно малая площадка, проходящая
через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() .
.
Так как циркуляция вектора
![]() по замкнутому контуру равна
по замкнутому контуру равна![]() ,
,![]() ,
то
,
то
![]() ,
или
,
или![]() .
(1.1.4)
.
(1.1.4)
Так как направление
![]() выбрано произвольно, то проекция
выбрано произвольно, то проекция![]() на любые направления равна 0, поэтому
из (1.1.4)
на любые направления равна 0, поэтому
из (1.1.4)![]() во всех точках
электростатического поля, то есть
электростатическое поле является
безвихревым.
Этот результат можно получить и из
теоремы Стокса. Выражения (1.1.3) и (1.1.4)
эквивалентны.
во всех точках
электростатического поля, то есть
электростатическое поле является
безвихревым.
Этот результат можно получить и из
теоремы Стокса. Выражения (1.1.3) и (1.1.4)
эквивалентны.
