
- •2. Динамика материальной точки
- •2.1.Границы применимости классической механики
- •2.2. Инерциальные системы отсчета и первый закон ньютона
- •2.3. Масса, импульс, сила
- •2.3. Второй закон ньютона. Уравнение движения материальной точки
- •2.4. Третий закон ньютона и закон сохранения импульса
- •2.5. Центр масс механической системы, закон движения центра масс
- •2.6. Преобразования галилея. Принцип относительности галилея
- •2.7. Силы
- •2.8. Упругие силы. Идеально упругое тело. Упругие напряжения и деформации. Закон гука. Модуль юнга
- •2.9. Силы сопротивления
- •2.10. Гравитационные силы. Закон всемирного тяготения
- •2.11.Сила тяжести и вес
- •2.12. Движение тел с переменной массой. Уравнение мещерского. Формула циолковского
2.11.Сила тяжести и вес
 Под действием
силы притяжения к Земле все тела падают
с одинаковым относительно поверхности
Земли ускорением
Под действием
силы притяжения к Земле все тела падают
с одинаковым относительно поверхности
Земли ускорением
![]() .
Это означает, что в системе отсчета,
связанной с Землей, на всякое тело массы
.
Это означает, что в системе отсчета,
связанной с Землей, на всякое тело массы
![]() действует
сила
действует
сила![]() ,
называемая силой тяжести. Когда тело
покоится относительно поверхности
Земли, сила
,
называемая силой тяжести. Когда тело
покоится относительно поверхности
Земли, сила![]() уравновешивается реакцией
уравновешивается реакцией
![]() подвеса или опоры, удерживающих тело
от падения
подвеса или опоры, удерживающих тело
от падения
![]() .
По третьему закону Ньютона тело в этом
случае действует на подвес или опору с
силой равной -
.
По третьему закону Ньютона тело в этом
случае действует на подвес или опору с
силой равной -![]() ,
т.е. с силой
,
т.е. с силой
![]() .
.
Сила
![]() ,
с которой тело действует на подвес или
опору, называется весом тела. Эта сила
равна
,
с которой тело действует на подвес или
опору, называется весом тела. Эта сила
равна
![]() лишь в том случае, когда тело и опора
(или подвес) неподвижны относительно
Земли. В случае их движения с ускорением
лишь в том случае, когда тело и опора
(или подвес) неподвижны относительно
Земли. В случае их движения с ускорением![]() вес
вес
![]() не будет равен
не будет равен
![]() .
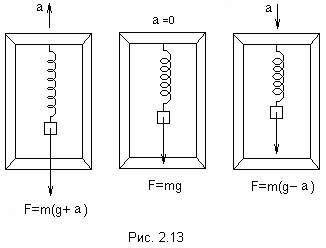
Рассмотрим пример (рис.2.13). Подвес в виде
укрепленной на рамке пружины движется
вместе с телом с ускорением
.
Рассмотрим пример (рис.2.13). Подвес в виде
укрепленной на рамке пружины движется
вместе с телом с ускорением![]() .
Уравнение движения тела имеет вид
.
Уравнение движения тела имеет вид
![]() ,
,
где
![]() –
реакция подвеса, т.е. сила, с которой
пружина действует на тело. По третьему
закону Ньютона тело действует на пружину
с силой –
–
реакция подвеса, т.е. сила, с которой
пружина действует на тело. По третьему
закону Ньютона тело действует на пружину
с силой –![]() ,
которая по определению представляет
собой вес тела
,
которая по определению представляет
собой вес тела
![]() .
Тогда
.
Тогда
![]() .
(2.24)
.
(2.24)
Эта формула определяет вес тела в общем случае.
Предположим, что тело и подвес движутся в вертикальном направлении (демонстрация 5). Спроектировав (2.24) на направление отвеса, получаем:
![]() .
.
Знак «+»
соответствует ускорению, направленному
вверх, а знак «- » - ускорению, направленному
вниз. При свободном падении рамки
![]() и
и
![]() =0.
Тело находится в невесомости.
=0.
Тело находится в невесомости.
Не следует
путать силу тяжести и вес. Эти силы
приложены к разным телам:
![]() –к телу, а
–к телу, а
![]() – к опоре. Сила
– к опоре. Сила
![]() всегда равна
всегда равна![]() ,
независимо от того, движется тело или
покоится, сила же веса
,
независимо от того, движется тело или
покоится, сила же веса
![]() зависит от ускорения, с которым движутся
опора и тело, и может быть как больше,
так и меньше
зависит от ускорения, с которым движутся
опора и тело, и может быть как больше,
так и меньше
![]() .
.
2.12. Движение тел с переменной массой. Уравнение мещерского. Формула циолковского
![]()
 В ньютоновской
механике масса считается независящей
от скорости, однако это вовсе не означает,
что она должна оставаться постоянной
в процессе движения тела. Она может
меняться, например, при обмене веществом
между телом и оружающей средой. Типичным
примером движения тела переменной массы
является реактивное движение. В процессе
работы установленного на ракете двигателя
продукты сгорания топлива выбрасываются
через сопло двигателя, и масса ракеты
постепенно уменьшается.
В ньютоновской
механике масса считается независящей
от скорости, однако это вовсе не означает,
что она должна оставаться постоянной
в процессе движения тела. Она может
меняться, например, при обмене веществом
между телом и оружающей средой. Типичным
примером движения тела переменной массы
является реактивное движение. В процессе
работы установленного на ракете двигателя
продукты сгорания топлива выбрасываются
через сопло двигателя, и масса ракеты
постепенно уменьшается.
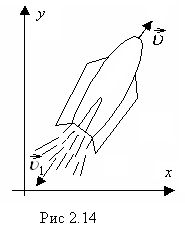
Основное
уравнение динамики материальной тела
переменной массы было получено И.В.
Мещерским. Рассмотрим систему, состоящую
из поступательно движущегося тела
переменной массы и отделяющихся от него
частиц (рис.2.14). В момент времени
![]() масса тела равна
масса тела равна
![]() ,
его скорость
,
его скорость
![]() ,
полный импульс системы равен
,
полный импульс системы равен
![]() .
От тела отделяются частицы со скоростью
.
От тела отделяются частицы со скоростью
![]() .За
время
.За
время
![]() масса отделившихся частиц составила
масса отделившихся частиц составила
![]() ,
а масса тела стала равна
,
а масса тела стала равна
![]() ,
скорость тела увеличилась до значения
,
скорость тела увеличилась до значения
![]() ,
тогда изменение импульса системы за
время
,
тогда изменение импульса системы за
время![]() равно
равно![]() .
Раскрыв
скобки и пренебрегая величиной
.
Раскрыв
скобки и пренебрегая величиной
![]() ,
получаем
,
получаем
![]() ,
или
,
или![]() ,
где
,
где![]()
– скорость отделяющихся частиц по отношению к рассматриваемому телу (относительная скорость). Подставив последнее выражение в закон изменения импульса (2.5), получим уравнение Мещерского:
![]()
векторная величина
![]() имеет
размерность силы и называется реактивной
силой. Положив в этом уравнении
имеет
размерность силы и называется реактивной
силой. Положив в этом уравнении![]() ,
получим формулу Циолковского для
движения ракеты под действием одной
только реактивной тяги:
,
получим формулу Циолковского для
движения ракеты под действием одной
только реактивной тяги:
![]()
где
![]() -
скорость истечения продуктов сгорания
из сопла ракеты, измеренная относительно
ракеты. Если начальная скорость ракеты
равна нулю, а траектория – прямая линия,
то скорости
-
скорость истечения продуктов сгорания
из сопла ракеты, измеренная относительно
ракеты. Если начальная скорость ракеты
равна нулю, а траектория – прямая линия,
то скорости
![]() и
и
![]() направлены противоположно, и в проекции
на направление движения ракеты получаем
направлены противоположно, и в проекции
на направление движения ракеты получаем
![]() или
или![]() .
.
Если
![]() –стартовая скорость ракеты, а
–стартовая скорость ракеты, а
![]() – конечная масса ракеты после окончания
работы двигателей вследствие выгорания
всего топлива,
– конечная масса ракеты после окончания
работы двигателей вследствие выгорания
всего топлива,
![]() -
масса топлива, тогда интегрируя последнее
выражение, получим максимальную скорость
ракеты:
-
масса топлива, тогда интегрируя последнее
выражение, получим максимальную скорость
ракеты:
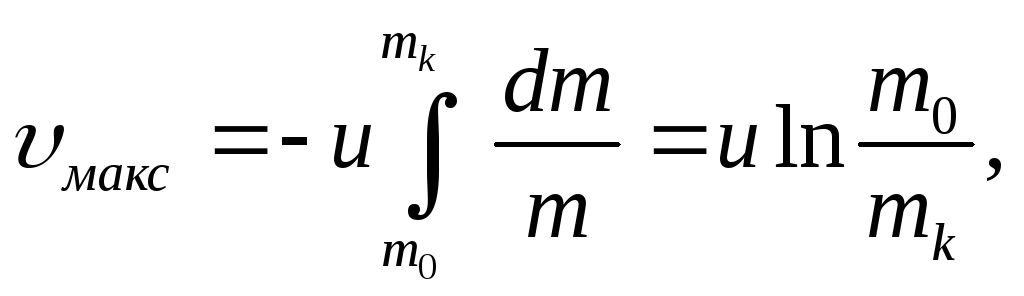 или
или
![]()
Эта формула называется формулой Циолковского.
