2.6. Преобразования галилея. Принцип относительности галилея

Рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью . Одну из систем, обозначенную на рис.2.5 буквой , будем условно считать неподвижной. Тогда вторая системабудет двигаться прямолинейно и равномерно. Выберем координатные оси системы и оси системы так, чтобы оси и совпадали, а оси и , а также и были параллельны друг другу.

Найдем связь между координатами некоторой точки в системе и координатами той же точки в системе . Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рис.2. 5,

, .

В классической механике считается, что время в обеих системах течет одинаковым образом, . Тогда получаем совокупность четырех уравнений, называемых преобразованиями Галилея:

, ,. (2.14)

Продифференцировав выражения (2.14) по времени, найдем связь между скоростями точки по отношению к системам отсчета и:

. (2.15)

В векторной форме . (2.16)

Формулы (2.15) и (2.16) выражают правило сложения скоростей в классической механике. При этом следует помнить, что выражения (2.15) справедливы лишь в случае выбора осей, показанных на рис.2.5. Выражение (2.16) справедливо при любом выборе осей. Продифференцировав (2.16) по времени, получаем:

(2.17)

- ускорение тела во всех инерциальных системах отсчета одинаково. Это означает, что и силы, действующие на тело в инерциальных системах отсчета одинаковы. Следовательно, уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой, т.е. инвариантны к преобразованиям Галилея. С механической точки зрения все инерциальные системы отсчета совершенно эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Это означает, что никакими механическими опытами, проведенными в пределах данной системы отсчета, нельзя установить, находится ли она в состоянии покоя или движется прямолинейно и равномерно. Эти положения носят название принципа относительности Галилея.

2.7. Силы

В современной физике различают четыре вида взаимодействий: гравитационное (вызванное всемирным тяготением), электромагнитное (осуществляемое через электрические и магнитные поля), сильное или ядерное (обеспечивающее связь частиц в атомном ядре) и слабое (проявляющееся при распаде элементарных частиц).

В классической механике имеют дело с гравитационными и электромагнитными силами, а также с упругими и силами трения. Два последних вида сил определяются характером взаимодействия между молекулами вещества и имеют электромагнитное происхождение.

Гравитационные и электромагнитные силы являются фундаментальными, их нельзя свести к другим, более простым силам. Упругие силы и силы трения не являются фундаментальными.

2.8. Упругие силы. Идеально упругое тело. Упругие напряжения и деформации. Закон гука. Модуль юнга

Всякое реальное тело под действием приложенных к нему сил деформируется,

т.е.изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый предел, называемый пределом упругости. Тело, в котором возникают только упругие деформации, называется абсолютно упругим.

Если после прекращения действия сил форма и размеры тела не восстанавливаются, говорят о неупругой деформации.

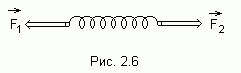
Рассмотрим пружину, имеющую в недеформированном состоянии длину , и приложим к ее концам равные по величине, противоположно направленные силы и(рис.2.6). Под действием этих сил пружина растянется на некоторую величину , после чего наступит равновесие. В состоянии равновесия внешние силы и будут уравновешены упругими силами, возникшими в пружине в результате деформации. При небольших деформациях удлинение пружины оказывается пропорциональным растягивающей силе:

(2.18)

-это закон Гука. Здесь- коэффициент жесткости пружины.

Упругие натяжения возникают во всей пружине. Любая часть пружины действует на другую часть с силой, определяемой формулой (2.18). Поэтому, если разрезать пружину пополам, та же по величине упругая сила будет возникать в каждой из половин при в два раза меньшем удлинении. Таким образом, при заданных материале пружины и размерах витка величина упругой силы определяется не абсолютным удлинением пружины , а относительным удлинением

При сжатии пружины также возникают упругие натяжения, но другого знака. Обобщим формулу (2.18) следующим образом. Закрепим один конец пружины неподвижно (рис.2.7), а удлинение пружины будем рассматривать как координату другого конца, отсчитываемую от его положения, отвечающего недеформированной пружине. Подбудем понимать проекцию на осьупругой силы. Тогда можно записать:

. (2.19)

Из рис.2.7 видно, что проекция упругой силы на ось и координатавсегда имеют разные знаки.

Однородные стержни ведут себя при растяжении или одностороннем сжатии подобно пружине. Если к концам стержня приложить направленные вдоль его оси силы и , действие которых равномерно распределено по всему сечению, то длина с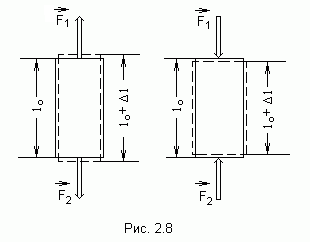тержня получит положительное ( при растяжении) или отрицательное (при сжатии) приращение (рис.2.8).Деформация стержня характеризуется относительным изменением длины:

Экспериментально доказано, что для стержней из данного материала относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:

. (2.20)

Коэффициент пропорциональности  называется коэффициентом упругой податливости.

Величина, равная отношению силы к площади поверхности, на которую действует сила, называется напряжением. В результате взаимодействия частей тела друг с другом напряжение передается во все точки тела и весь объем стержня оказывается в напряженном состоянии. Если сила направлена по нормали к поверхности, напряжение называется нормальным и обозначается . Если сила направлена по касательной к поверхности, возникает тангенциальное напряжение .

В выражении (2.20) , поэтому.

Величина, обратная упругой податливости, называется модулем Юнга С учетом сказанного, . Модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение было бы равно единице.

Решив записанные уравнения относительно F получаем: .

Это закон Гука для стержня.