22. Условный экстремум функции

Пусть у функции аргументы являются не независимыми переменными, а связаны между собойсоотношениями:

Эти соотношения называются условиями связи. Пусть координаты точкиудовлетворяют этим уравнениям.

Говорят, что функция имеет в точкеусловный (относительный) минимум(максимум) при условиях связиесли существует такая окрестность точки, что для любой точкииз этой окрестности, координаты которой удовлетворяют заданным условиям связи, выполняется неравенство.

Иначе говоря, условный(относительный) максимум(минимум) – это наибольшее (наименьшее) значение функции в точкепо отношению не ко всем точкам из некоторой окрестности точки, а только к тем из них, которые связаны между собой условиями связи.

Задачу отыскания условного экстремума функции можно решить двумя способами.

1. Метод исключения. Если уравнения связи можно разрешить относительно части переменных. Найденные выражения подставляются в исследуемую функцию, тем самым задача нахождения условного экстремума сводится к исследованию на экстремум функции одной переменной. Рассмотренный выше пример, когда мы исследовали заданную функцию на границе области, по сути своей, был на нахождение условного экстремума функции. И решали мы его именно методом исключения.

2. Метод Лагранжа. Этот метод обычно используется, когда уравнения связи неразрешимы относительно переменных. В таком случае задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа:

.

Коэффициенты называются множителями Лагранжа.

Необходимое условие экстремума выражается системой уравнений:

Решая эту систему, находим точки , подозрительные на экстремум. Их может быть несколько.

Достаточным условием экстремума в каждой из исследуемых точек является положительная (минимум) или отрицательная (максимум) определенность второго дифференциалафункции Лагранжа в этой точке.

Рассмотрим два метода решения задачи об условном экстремуме функции на примерах.

Пример 20. Методом исключения части переменных найти экстремум функции

(1)

при условиях связи

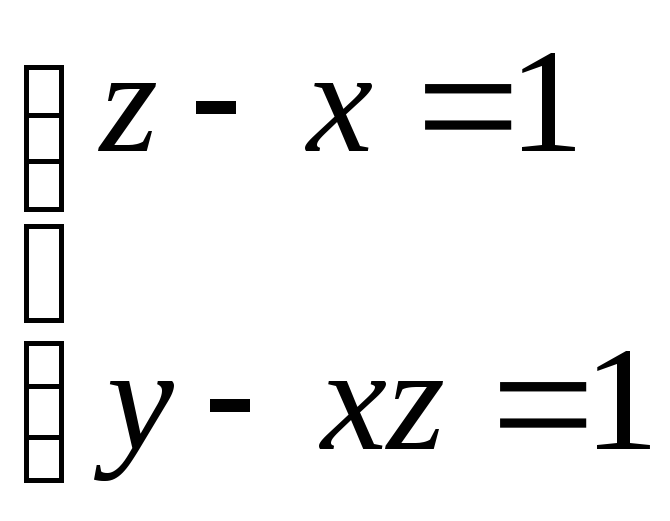(2)

Решение.Решая систему уравнений (2) относительно, находим

(3)

Подставляя выражения (3) в равенство (1), приходим к функции одной переменной :

,

для которой рассмотрим задачу о безусловном экстремуме. Так как при, то функцияимеет единственную точку возможного экстремума. Поскольку вторая производная в этой точке, то в точкефункцияимеет минимум. Подставляяв (3), находим соответствующие значенияи:,. Итак, функция (1) при условиях связи (2) имеет в точкеминимум, причём

Пример 21. Методом Лагранжа найти экстремум функции (1) при условиях связи (2).

Решение. Составим функцию Лагранжа

и рассмотрим систему уравнений:

Она имеет единственное решение: , т.е.– единственная точка возможного экстремума функции (1) при условиях связи (2). Отметим, что в окрестности точкисистема (2) определяет единственную пару неявных функций. Хотя в данном случае их легко найти в явном виде, нам эти явные выражения не понадобятся. Предполагая, что в систему (2) подставлено её решение, и дифференцируя полученные тождества, приходим к равенствам:

(4)

Теперь вычислим второй дифференциал функции Лагранжа:

и подставим и выражение (4) для; получаем

Отсюда следует, что функция (1) при условиях связи (2) имеет в точке условный минимум.

Пример 22. Найти наименьшее значение для суммы четырех положительных чисел при условии, что их произведение сохраняет постоянную величину, т.е..

Решение. Составим функцию Лагранжа

и рассмотрим систему уравнений:

Из первых четырех равенств следует, что

,

поэтому, учитывая условие связи, получаем, что

. .

Подставим найденное значение в выражение для функции Лагранжа и найдем ее второй дифференциал в точке :

.

Продифференцируем условие связи в той же точке:

,

.

Выразив из последнего, например, и подставив в выражение для второго дифференциала функции Лагранжа, получим, что

Очевидно, что выражение, стоящее справа, положительно при любых значениях дифференциалов переменных, следовательно, в данной точке функция Лагранжа будет достигать минимума. Тогда и заданная функция в точке с координатами >0 будет достигать требуемого, а именно: своего наименьшего значения

при заданном условии .

53