21. Наибольшее и наименьшее значения функции

Пусть функция определена и непрерывна в некоторойограниченной замкнутойобластиD и имеет в ней, за исключением, быть может, отдельных точек, конечные частные производные.

Наименьшее или наибольшее значение функции в заданной области называется абсолютным экстремумом функции(соответственно,абсолютным минимумом или абсолютным максимумом) в этой области.

Теорема Вейерштрасса.Функция, непрерывная в ограниченной и замкнутой области, достигает в ней своих наименьшего и наибольшего значений.

Теорема.Абсолютный экстремум функции вограниченной замкнутойобласти достигается либо в стационарной (или критической) точке функции, принадлежащей этой области, либо в граничной точке области.

Поэтому для отыскания наибольшего и наименьшего значений функции в областиD нужно:

найти все внутренние точки, «подозрительные на экстремум», а именно: стационарные или критические и вычислить значения функции в них,
найти наибольшее и наименьшее значение функции на линиях, образующих границу области,
сравнить полученные значения функции внутри области со значениями функции на границе: наибольшее из них будет наибольшим значением функции во всей области D, а наименьшее – наименьшим.

Пример 19.Найти наибольшее и наименьшее значения функции в замкнутой области, заданной неравенствами,,.

Решение.Данная функция непрерывна на всей плоскости. Заданная область – замкнутая и ограниченная, так как представляет собой треугольник, лежащий в первой четверти координатной плоскости, ограниченный координатными осями и прямой . Следовательно, по теореме Вейерштрасса заданная функция принимает на этой области свои наибольшее и наименьшее значения. Найдем их.

1. Находим стационарные точки внутри области задания функции

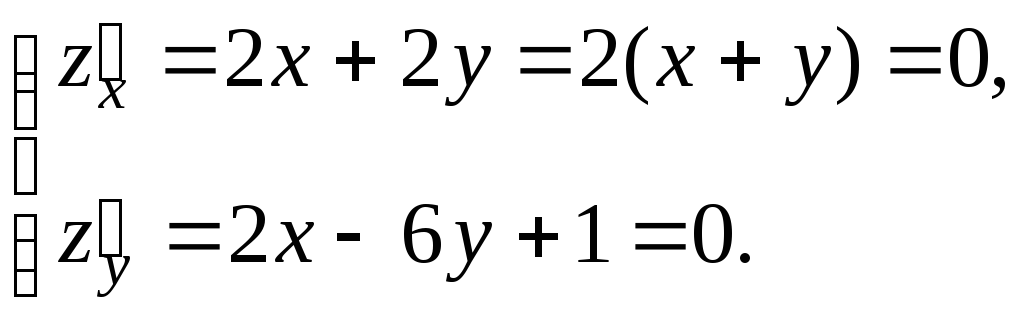
Решаем полученную систему: ,.

Других стационарных точек нет. Так как точка лежит во второй четверти координатной плоскости, то она не принадлежит рассматриваемой области, и значение функции в ней не вычисляем и не учитываем.

2. Исследуем функцию на границе области. Поскольку граница состоит из трех участков, описанных тремя разными уравнениями, то будем исследовать функцию на каждом участке отдельно.

a). Исследуем функцию на участке ОА,гдеА(1,0).Уравнением этого отрезка, или уравнением связи. является. Поэтому на этом участке границы после подстановки в выражение для функции уравнения границы функция будет иметь вид. Это уже функция одной переменной. Она непрерывна и дифференцируема всюду. Поэтому на замкнутом отрезке она принимает свои наибольшее и наименьшее значения либо в стационарной точке внутри отрезка, либо на его концах.

Из полученного уравнения сразу видно, что функция возрастает на ОА от 0 до 1. Следовательно, наименьшее значение функция будет иметь при, т.е. в начале координат, , а наибольшее – при, т.е. в точкеА,

б). Исследуем функцию на участке ОВ, гдеВ(0,1). Уравнением границы является уравнение.Поэтому на этом участке границы функция принимает вид:

Как и в предыдущем пункте, находим стационарные точки функции, принадлежащие отрезку, вычисляем значения функции в этих точках и на концах и сравниваем.

, .