Предел и непрерывность функции

7. Предел функции нескольких переменных

Говорят, что последовательность точек с координатами стремится к точке сгущения некоторого множества , если

…, .

При этом расстояние между точками последовательности и точкой , когда неограниченно возрастает, стремится к нулю, т.е.

так как

= = .

Верно и обратное: если то последовательность точек стремится к точке .

Пусть функция определена в некоторой окрестности D точки , за исключением, быть может, самой точки .

По аналогии с определением предела функции одной переменной, говорят, что функция имеет пределом число при стремлении переменных , соответственно, к , если для каждого сколь угодно малого наперед заданного положительного числа (эпсилон) существует такое число , что

(2)

как только

, …, .

При этом точка предполагается взятой из D и отличной от . Итак, неравенство (2) для функции должно выполняться во всех точках множества D, лежащих в достаточно малой окрестности

точки , но исключая саму эту точку (если она принадлежит D). В этом случае обозначают предел функции так:

.

В геометрических терминах можно перефразировать данное определение следующим образом.

Говорят, что число является пределом функции при стремлении точки к точке (или – пределом функции в точке ), если для каждого сколь угодно малого наперед заданного положительного числа существует такое число , что

()

как только расстояние между точками .

Как и выше, точка предполагается взятой из D и отличной от , а неравенство для функции должно выполняться во всех точках множества D, лежащих в достаточно малой сферической окрестности точки , за исключением самой этой точки.

Обозначение предела функции, соответствующее данному определению:

.

Два приведенных выше определения предела функции многих переменных являются равносильными.

Аналогично устанавливается понятие о бесконечном пределе функции: неравенство (2) заменяется на

, если , и

, если ,

где – произвольное наперед заданное сколь угодно большое положительное число.

Распространим понятие точки сгущения на тот случай, когда все координаты (или некоторые из них) этой точки бесконечны:

Точка является для области D точкой сгущения, если в этой области найдутся точки со сколь угодно большими (положительными) координатами.

Тогда говорят, что функция имеет пределом число при стремлении переменных к , если для каждого сколь угодно малого наперед заданного положительного числа существует такое число , что

как только

.

Обозначаем это следующим образом:

.

Условие, необходимое и достаточное для существования предела функции в точке формулирует следующая теорема.

Теорема. Если из множества D извлечь последовательность отличных от точек, сходящуюся к , то числовая последовательность , состоящая из соответствующих значений функции, всегда сходится к .

8. Повторные пределы

Наряду с рассмотренным пределом функции при одновременном стремлении всех ее аргументов к их пределам, определим несколько иной предел для функции многих переменных, который получается в результате ряда последовательных предельных переходов по каждому ее аргументу в том или ином порядке. Будем называть такой предел повторным, тогда как рассмотренный ранее — кратным (или двойным, тройным и т.д. – при , соответственно).

Для простоты ограничимся случаем функции двух переменных . Пусть область D изменения переменных и такова, что независимо от может принимать любое значение из некоторого множества , для которого служит точкой сгущения, но не принадлежит ему, а переменная , тоже независимо от , – любое значение из множества с не принадлежащей ему точкой сгущения . Тогда область D .

Если при любом фиксированном для функции (которая при фиксированном будет функцией одной переменной ) существует предел при , то он, этот предел, вообще говоря, будет зависеть от зафиксированного :

.

Если теперь существует предел функции при ,

,

то он и будет являться одним из повторных пределов функции .

Если предельные переходы произвести в другом порядке, то получим другой повторный предел этой же функции:

.

Вообще говоря, повторные пределы не обязательно равны между собой. Может случиться и так, что один из повторных пределов существует, а другой – нет.

Для иллюстрации этого рассмотрим несколько примеров. Пусть в области заданы функции:

1. и . Тогда

,

,

а ,

.

2. 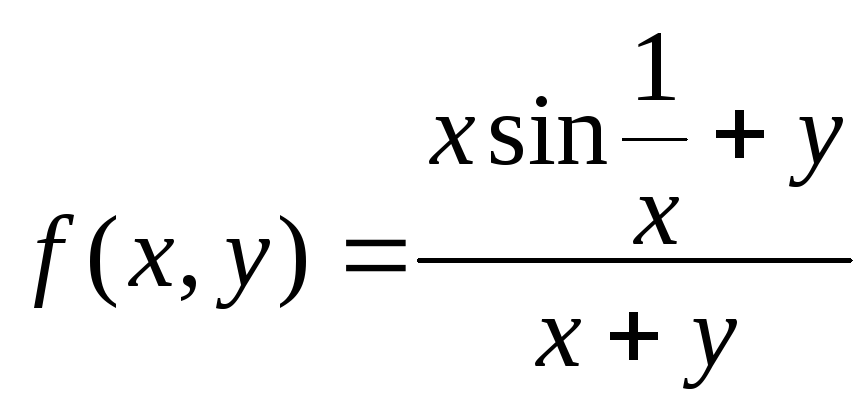3. .

Здесь в обоих случаях существует повторный предел , но нет повторного предела . А в последнем примере нет и простого предела . Проверьте!

Связь между двойными и повторными пределами устанавливает следующая теорема.

Теорема. Если

1. существует двойной предел (конечный или нет)

и

2. при любом существует конечный простой предел по

,

то существует повторный предел

и равен двойному:

=.

Если, наряду с условиями 1 и 2 теоремы, при любом существует конечный простой предел по

,

то существует и второй повторный предел, который тоже равен двойному, т.е.

,

тем самым мы определили условия, при которых оба повторных предела равны.

Из этой теоремы становится ясно, что в примерах 1 и 2 двойной предел не существует, а в примере 3 он существует и равен 0, откуда следует, что выполнение условия 1) теоремы не влечет за собой выполнения условия 2).

Замечание. Существование двойного предела не является необходимым условием для равенства повторных пределов.

Рассмотрим еще один пример. Функция определена на всей плоскости за исключением точки .

Возьмем две сходящиеся к последовательности точек из области :

и .

Построим две соответствующие последовательности значений функции:

и .

Очевидно, что эти последовательности «сходятся» к разным значениям. Отсюда следует, что у данной функции двойного предела в точке не существует.

Рассмотрим повторные пределы этой функции:

и .

, ,

, .

Мы видим, что оба повторных предела функции в точке существуют и оба равны 0, хотя двойного предела данная функция в данной точке не имеет.

Примеры.

1. , .

2. , .

3. , .

4. .

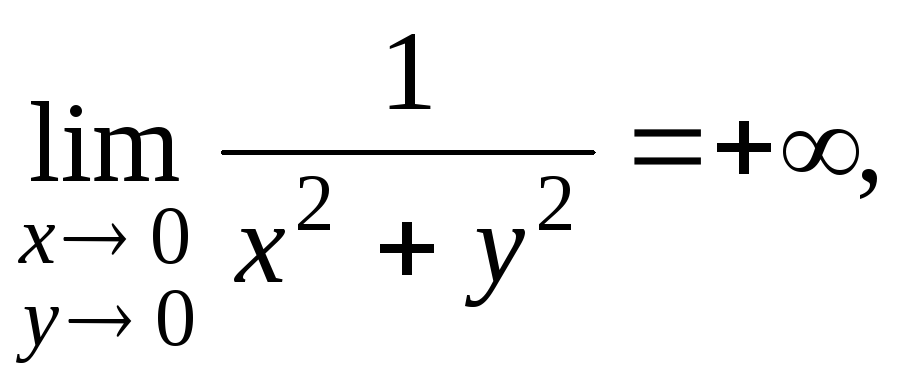
9. Непрерывность

Пусть функция определена в некотором множестве D точек мерного пространства, и – точка сгущения этого множества, принадлежащая самому множеству, т.е. D.

Говорят, что функция непрерывна в точке , если имеет место равенство

, (3)

в противном случае говорят, что функция в данной точке терпит разрыв.

На языке «ε – δ» (эпсилон – дельта) определение непрерывности функции в точке будет звучать так: функция непрерывна в точке , если для каждого сколь угодно малого наперед заданного положительного числа найдется такое число , что

(4)

как только расстояние между точками будет удовлетворять неравенству

, или

, …, . (5)

При этом точка предполагается взятой из D и, в частности, может совпадать с точкой . По причине того, что предел функции в точке должен быть равен значению функции в этой точке, требование, чтобы не совпадала c становится лишним.

Рассматривая разности в (5) как приращения независимых переменных, а разность в (4) – как приращение функции, можно данное определение перефразировать следующим образом:

Функция непрерывна, если бесконечно малым приращениям независимых переменных соответствует бесконечно малое приращение функции.

Если функция непрерывна в каждой точке множества D, то говорят, что она непрерывна в D.

Все основные теоремы о непрерывных функциях, приводимые для функций одной переменной, распространяются и на случай функций нескольких переменных.

Теорема. Сумма, разность, произведение и частное непрерывных в точке функций есть непрерывная в этой точке функция, если, конечно, в случае частного, функция, стоящая в знаменателе, в точке не обращается в ноль.

Функцию будем называть элементарной функцией переменных, если она может быть получена из этих переменных и констант при помощи конечного числа алгебраических операций.

Как и в случае одной переменной, элементарные функции непрерывны внутри своих естественных областей определения. Суперпозиция (сложная функция) непрерывных функций является непрерывной функцией в своей области определения.

Примерами элементарных функций, непрерывных на всей плоскости, могут служить функции

,

.

Функция , являясь суперпозицией элементарных функций, тоже непрерывна на всей плоскости. А функция определена и непрерывна только в тех точках, в которых дробь неотрицательна, а знаменатель этой дроби не равен нулю.

18