В разделе математики «Теория функции вещественной переменной» мы изучали совместное изменение двух переменных, одна из которых зависелаот другой. В этом случае значениемнезависимой переменнойвполне определялось и значениезависимой переменнойили функции. В науке и в жизни, однако, нередки случаи, когданезависимых переменныхоказывается несколько. В этом случае для определения значения функции необходимо предварительно установить значения, которые могут принимать совместно все независимые переменные.

«Функции многих переменных» – это раздел математики, развивающий и обогащающий наши представления о количественных соотношениях, которые выражают наиболее важные закономерности в естественных науках и экономике.

Сложности, возникающие при изучении это раздела, связаны, в частности, с тем обстоятельством, что большинство используемых терминов (функция, независимая переменная, область определения функции и т.д.) использовались и ранее, при изучении раздела «Функции одной действительной переменной». Но теперь большинство из них нужно определить заново. При этом, несмотря на внешнюю похожесть определений, в них появляется ряд особенностей, новое, более богатое содержание. То же самое касается и теорем, которые приводятся в этом разделе. Существенно ограничиваются и наши возможности наглядных иллюстраций с помощью изображения графиков функций. Если для случая функции двух независимых переменных эта проблема как-то решается, то когда переменных больше трех, сделать это уже практически невозможно. Тем не менее, не следует пренебрегать наглядными примерами. В самом деле, если вы разобрались с функциями двух переменных, то большинство утверждений, касающихся функций с числом аргументов , можно проиллюстрировать примерами, использующими функции двух переменных.

Основные понятия

1. Области. Граничные точки. Замкнутые области

Множество точек называется плоским множеством, если его точки лежат в одной плоскости.

Плоское множество называется ограниченным, если существует круг, внутри которого оно содержится. Отрезок, треугольник, многоугольник и т.п. являются ограниченными множествами. Прямая не является ограниченным множеством.

Окрестностью точки P называется внутренность любого круга с центром в . Точканазываетсявнутренней точкой множества , если существует ее окрестность, целиком принадлежащая множеству . Множество, состоящее лишь из внутренних точек, называется открытой областью, или, короче, областью. Внутренние части треугольника, круга, эллипса, квадрата являются примерами таких областей.

«Кривая», состоящая из конечного числа «прямолинейных отрезков», называется «ломаной».

Область называется связной, если любые две ее точки можно соединить ломаной, целиком лежащей в данной области. Все вышеупомянутые области являются связными. На рис. 1 представлено несколько связных областей на плоскости. Примером несвязной области может служить множество точек круга, если исключить из него его диаметр.

Точка , не принадлежащая области, называетсяграничной, если любая ее окрестность содержит точки, принадлежащие области . Множество всех граничных точек областиназываетсяграницей области и обозначается. Границей для внутренности круга служит окружность.

Множество, образованное областью и ее границей, называется замкнутой областью.

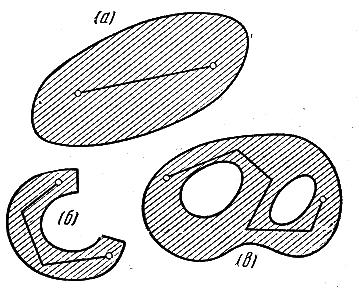
Рис. 1

Точка называетсяточкой сгущения для множества , если в каждой ее окрестности есть точки из множества, отличные от. В частности, любая граничная точка является точкой сгущения.

Сравним введенные выше понятия с похожими понятиями для точечных множеств на числовой прямой .

Окрестностями точки являются интервалы вида, где. Области будут представлены всевозможными объединениями интервалов. Граничные точки – это концы замкнутых отрезков.

Заметим, что роль окрестностей для точек плоского множества могут играть не только внутренние части некоторых кругов, но и квадратов с центром в точке. Действительно, если точкаокружена некоторым кругом радиуса, то она будет лежать и внутри квадрата, вписанного в этот круг. Если же она «окружена» квадратом со стороной, то круг радиусас центром в точкебудет окрестностью точки. Поэтому, если дать определение внутренней точки множествана языке «квадратных» окрестностей, то это определение будет равносильно данному выше. Легко сообразить, что в качестве окрестностей можно использовать и прямоугольники.

2. Функции двух переменных и области их определения

Уточнение понятия функции в случае нескольких независимых переменных начнем со случая, когда этих переменных всего две.

Пусть – произвольное множество точек, лежащих в координатной плоскости . Говорят, что на множествеопределена функция, если каждой точкемножества – по некоторому правилу или закону – поставлено в соответствие одно определенное действительное число. Переменная(собластью изменения) называетсяфункцией независимых переменных и .

Множество пар , которым обычно является открытая или замкнутая область, называется областью определения функции. Сами переменные и – по отношению к их функции – называются ееаргументами. Функциональная зависимость между и обозначается, аналогично случаю одной независимой переменной,

, , и т.п.

Множество называетсяобластью значений (или изменения) функции . Если для функции одной переменной стандартной областью изменения аргумента являлся некоторый промежуток (конечный или бесконечный) числовой оси , то в случае функции двух переменных мы сталкиваемся с большим разнообразием и сложностью возможных областей изменения ее аргументов. В декартовой системе координат это может быть либо вся плоскость , либо ее часть.

Вот несколько примеров функций, заданных аналитически, т.е. с помощью формул, с указанием их областей определения. Формулы