
2_Элементы теории множеств
.pdf
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
|
Множество – основное математическое понятие. В |
|
обычной жизни его смысл заложен в словах: |
|
«совокупность», «класс», «стая», «табун», «стадо» и т.п. |
|
Теория множеств как математическая дисциплина создана |
|
немецким математиком Г. Кантором, которая получила |
|
признание в качестве самостоятельного раздела математики |
|
к 1890 году, когда были получены ее приложения в анализе |
|
и геометрии. Главная заслуга Георга Кантора заключается в |
|
установлении того факта, что понятие бесконечность |
|
является не абстракцией, придуманной философами, а |
|
реальностью; бесконечные совокупности предметов |
Георг Кантор |
существуют наравне с конечными. |
(1845 – 1918 гг.) |
Множество относится к математическим объектам, |
немецкий математик |
для которых нет строго определения. Мы можем лишь в |
|
какой-то мере дать описание основных его свойств. |
Кантор описывает множество следующим образом:
О п р е д е л е н и е . Множество S есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое.
Понятие множества. Способы задания множества
Мы под множеством будем понимать следующее:
О п р е д е л е н и е . Множество – набор (совокупность) определенных, различимых между собой объектов, рассматриваемых как единое целое, и обладающий некоторым общим свойством.
А, B, C и т.п. .
Объекты, составляющие данное множество, называют его
элементами.
х, a, b и т.п. .
Для того, чтобы указать, что х – элемент множества А, записывают х А и читают «х принадлежит А». Чтобы указать, что х не является элементом множества А, записывают х А и читают «х не принадлежит множеству А».
Для ряда числовых множеств в математике приняты стандартные обозначения:
Обозначения числовых множеств:
1)N – множество натуральных чисел.
2)Z – множество целых чисел.
3)Q – множество рациональных чисел (дроби).
4)R – множество действительных чисел
2
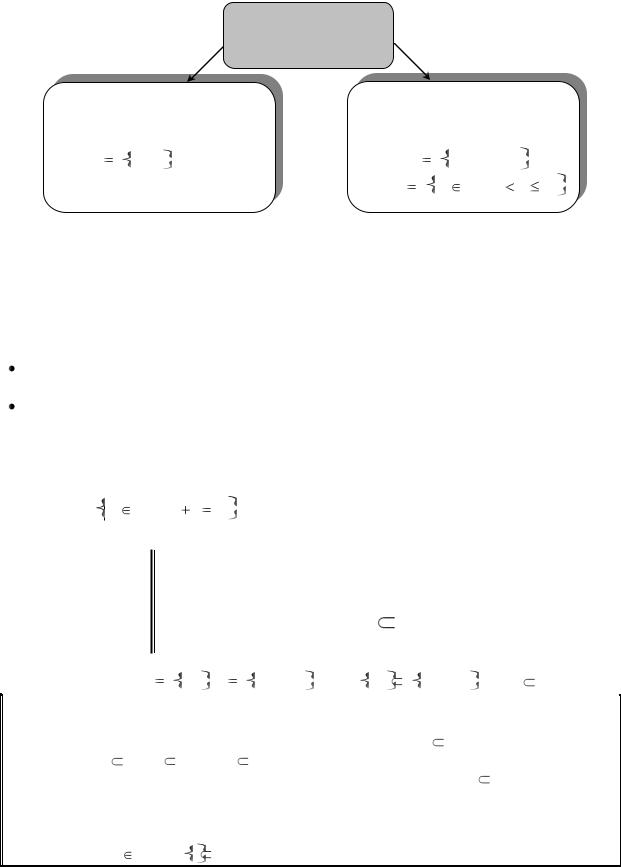
Существует два способа задания множества:
Способы задания множеств
Перечисление его |
|
Указания |
|
|||
элементов |
характеристического |
|||||
|
|
|
свойства |
|
||
|
|
|
|
|
||
пр: А 1, 2, 3 |
A |
|
a |
свойство |
|
|
|
|
пр: С |
|
|
||
|
|
х |
х N и 2 |
x 7 |
||
|
Рисунок 1. Способы задания множеств |
|
||||
Множества можно разделить на конечные и бесконечные. |
|
|||||
О п р е д е л е н и е . |
|
множеством называется |
множество, |
состоящее из |
||
Конечным |
||||||
|
конечного числа элементов. |
|
|
|
|
|
|
Множество называется бесконечным, если оно состоит из |
|||||
|
бесконечного числа элементов |
|
|
|
|
|
П р и м е р 1 . |
|
|
|
|
|
|
Конечные множества: множество букв алфавита, множество студентов 2 курса специальности «Юриспруденция» и т.д.
Бесконечные множества: множество натуральных чисел, множество точек прямой
ит.д.
Кконечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустым и обозначают Ø.
П р и м е р 2 .
Ø = х х R и x2 1 0 , поскольку среди действительных чисел нет решения данного уравнения.
О п р е д е л е н и е . Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется
подмножеством множества А.
|
|
|
|
В |
А |
|
|
|
|
(В включено в А). |
|||
|
П р и м е р 3 . |
|
|
|
|
|
|
Множество В |
2, 3 , А |
2, 3, 4, 5 , тогда 2, 3 |
2, 3, 4, 5 , т.е. В А. |
||
|
|
|
|
|
||
Основные свойства включений: |
|
|
|
|
||
1) |
Каждое множество есть подмножество самого себя: A A. |
|||||
2) |
Если A B , B |
C , то A |
C . |
|
|
|
3) |
Пустое множество есть подмножество любого множества: Ø A. |
|||||
4)Каждое не пустое множество A 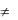 Ø имеет по крайней мере два различных подмножества: само А и пустое множество Ø.
Ø имеет по крайней мере два различных подмножества: само А и пустое множество Ø.
5)Каждый элемент множества А определяет некоторое подмножество множества
А: если a A , то a A .
3

О п р е д е л е н и е . Множества А и В называются равными (или совпадающими), если они состоят из одних и тех же элементов, т.е. А В и
ВА.
|
|
|
|
|
|
|
В А |
|
Если множества не равны, то пишут A |
B . |
|
|
|||||
П р и м е р 4 . |
|
|
|
|
|
|
|
|
Множества Х |
2, 3 и Y |
y |
|
y2 5y |
6 |
|
0 , где y 2 и y 3 удовлетворяют |
|
|
|
|||||||
уравнению y2 5y 6 0 , т.е. Y |
2, 3 , значит X |
Y . |
||||||
О п р е д е л е н и е . |
Множество |
всех подмножеств множества А называется |
||||||
|
множеством-степенью множества А. |
|||||||
P A |
П р и м е р 5 . |
|
|
Пусть Х |
2, 3 , тогда P X |
{ A, {2}, {3}, Ø}, т.е. если множество состоит из |
двух элементов, то множество-степень состоит из четырех подмножеств. |
||
Пусть Y |
2, 3, 4 , тогда P Y |
{ A, {2}, {3}, {4}, {2,3}, {3,4}, {2,4}, Ø}, т.е. |
если множество состоит из трех элементов, то множество-степень состоит из восьми подмножеств.
Таким образом, если конечное множество А состоит из n элементов, то число всех его подмножеств равно 2n .
О п р е д е л е н и е . Множество U называется универсальным для системы множеств А, B, C, …, если каждое множество системы является подмножеством U, т.е. A U , B U , C U , …. .
U |
Операции над множествами |
|
|
|
|
|
|
|
||||
|
Если имеются два (или |
|
|
|
|||||||
|
|
|
|
||||||||
|
более) множества, то на основе их |
|
|
|
|||||||
|
можно получить новые множества |
|
|
|
|||||||
|
при |
помощи |
операций |
|
|
|
|||||
|
(отношений) |
|
над |
|
ними. |
|
|
|
|||
|
Геометрически, |
для |
наглядного |
|
|
|
|||||
|
представления, данные отношения |
|
|
|
|||||||
|
можно |
представить при помощи |
|
|
|
||||||
|
кругов, |
которые один из первых |
|
|
|
||||||
|
использовал |
для |
решения |
задач |
|
|
|
||||
|
Г.Лейбниц, затем |
развил |
их |
|
Леонард Эйлер |
||||||
Джон Венн |
применение |
Леонард |
Эйлер |
и |
|
(1707 – 1783 гг.) |
|||||
особенного расцвета достигшие в |
|
немецкий математик |
|||||||||
(1843–1923) |
|
||||||||||
сочинениях |
английского |
логика |
|
|
|
||||||
английский логик |
|
|
|
||||||||
Джона |
Венна, |
поэтому |
такие |
схемы иногда называют |
|||||||
|
|||||||||||
Диаграммы Эйлера-Венна.
Диаграммы используются в математике, логике, менеджменте, особое применение они нашли в современной логико-математической теории «формальных нейронных сетей».
4

Мемориальное окно Джона Венна в Кембридже
На Диаграммах Эйлера-Венна универсальное множество U изображается в виде прямоугольника, его подмножества – в виде кругов (реже прямоугольников), а элементы принадлежащие данным подмножествам в виде точек (см. Рисунок 2).
U
x 
A a
B
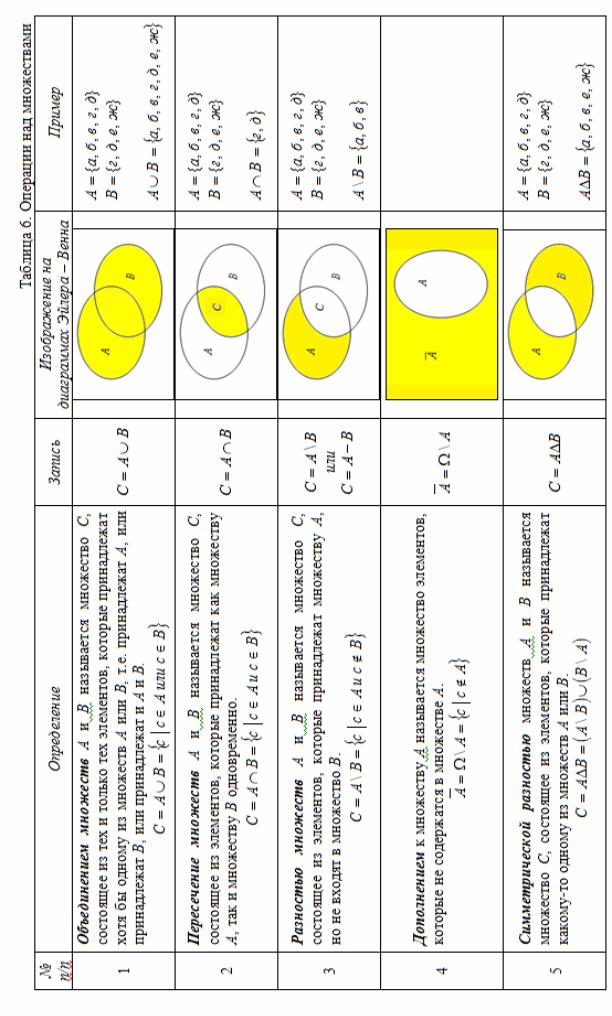
Рисунок 2. Пример диаграммы Эйлера-Венна Рассмотрим операции над множествами, некоторые
из которых (объединение и пересечение) аналогичны операциям сложения и умножения целых чисел.
Операции пересечение и объединение множеств выполняются для любой пары множеств. Операция дополнение имеет смысл для тех множеств, когда второе является подмножеством первого.
Следует провести аналогию между логическими операциями и операциями над множествами.
Высказывание |
|
Множество |
|||
|
(конъюнкция) |
Пересечение |
|||
|
(дизъюнкция) |
Объединение |
|||
|
|
(импликация) |
|
|
Разность \ |
|
|
(отрицание) |
|
|
( дополнение) |
|
|
|
|||
|
тавтология |
U (универсальное множество) |
|||
|
противоречие |
Ø (пустое множество) |
|||
Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы
алгебры множеств. Например, А В , A B \ C – формулы алгебры множеств.
5
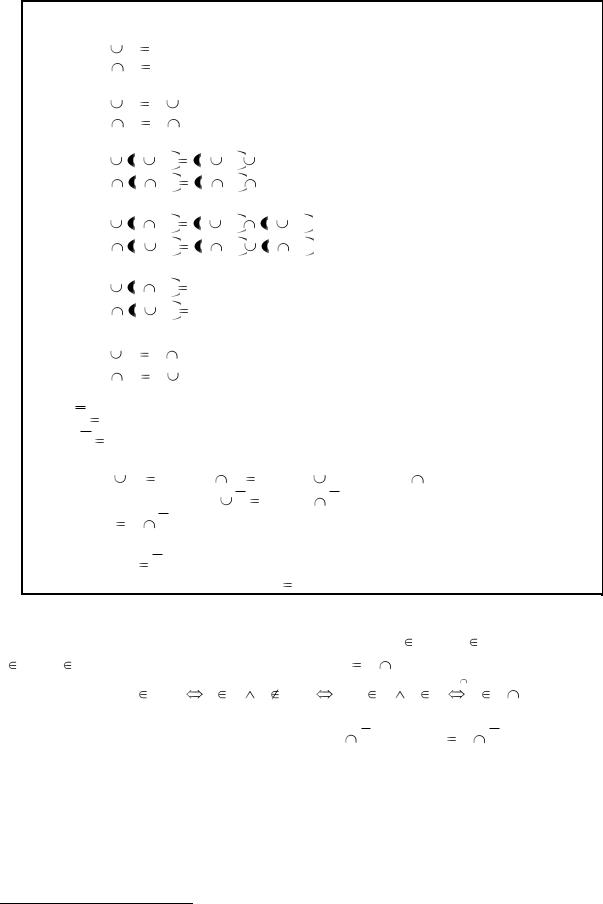
Основные законы над множествами
Законы: |
|
|
|
|
|
|
|
|
|
|
|
|
1) |
Закон идемпотентности: |
|
|
|||||||||
|
a) |
|
А |
А |
А |
|
|
|
|
|
||
|
б) А |
А |
А |
|
|
|
|
|
||||
2) |
Закон коммутативности: |
|
|
|||||||||
|
a) |
|
A |
B |
B |
A |
|
|
|
|||
|
б) A |
B |
B |
A |
|
|
|
|||||
3) |
Закон ассоциативности: |
|
|
|||||||||
|
a) |
|
A |
B |
C |
|
A |
B |
C |
|
||
|
б) A |
B |
C |
|
A |
B |
C |
|
||||
4) |
Закон дистрибутивности: |
|
||||||||||
|
a) |
|
A |
B |
C |
|
A |
B |
A |
C |
||
|
б) A |
B |
C |
|
A |
B |
A |
C |
||||
5) |
Закон поглощения: |
|
|
|
||||||||
|
a) |
|
A |
A |
B |
|
A |
|
|
|
||
|
б) A |
A |
B |
|
A |
|
|
|
||||
6) |
Закон де Моргана: |
|
|
|
||||||||
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
B |
A |
B |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) A |
B |
A |
B |
|
|
|
|||||
7)Закон двойного отрицания:
A A
8)U Ø
9)Законы для объединения, пересечения и дополнения:
а) A U U ; б) A U A ; в) A Ø = A; г) A Ø = Ø;
д) A A U ; е) A A  Ø
Ø
10) A \ B A B
11) Законы для разностей:
а) U \ A A ; б) A \ U 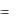 Ø; в) A \ Ø = A; г) Ø \ A
Ø; в) A \ Ø = A; г) Ø \ A 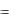 Ø;
Ø;
д) A \ A Ø
Доказательство каждого из перечисленных законов основано на определении равенства множеств и определений операций над множествами. Чтобы доказать некоторое
тождество A = B, нужно доказать, что, во-первых, |
если x |
|
А, то x |
В и, во-вторых, если |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x В, то x |
А. Докажем один из этих законов: |
A \ B |
A |
|
B . |
|
|
|
|
|
|
|
|
||||
|
|
|
def \ |
defдополнения |
|
|
|
|
|
|
def |
|
|
|
1. |
|
|
Пусть |
х |
A \ B х A |
х B |
|
х |
A |
х |
|
B |
х |
A |
B |
Таким |
||||
образом, |
мы |
взяли |
произвольный |
элемент |
х из |
A \ B |
и |
при |
помощи равносильных |
||||||||
преобразований получили, что он принадлежит A B , т.е. A \ B A B .
И действительно это так, проиллюстрируем это на диаграммах Эйлера-Венна (см.
Рисунок 3).
1 def – это действие по определению.
7

|
|
|
|
|
|
Правая часть |
|
|
|
|
|
|
|
|
|
|
|
Левая часть |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|||||
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
А |
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
В |
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
В |
= |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A \ B |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
A |
B |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Рисунок 3. Пример иллюстрации равенства множеств A \ B A |
B на диаграммах |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эйлера-Венна |
|
|
|
|
|
|
|
|
||||||||
|
|
П р и м е р 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Пусть |
|
|
А, |
|
В |
|
|
и |
С |
|
произвольные |
множества. |
|
Докажите, |
что |
||||||||||||||
A |
B |
C |
A |
B |
A |
C (закон дистрибутивности). |
|
|
|
|
|
|
|||||||||||||||||||
|
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
высказывание |
|
|
по закону дистрибутивности |
|||||
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
над высказываниями |
||||||
х A B C |
x A x B C |
|
|
|
|
x A |
|
x B |
x C |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
высказывание |
|
|
|
высказывание |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|||
|
x A x B x A x C |
|
|
|
x A B x A C |
x A B |
A C , т.е. |
||||||||||||||||||||||||
A |
B |
C |
|
A |
B |
A |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
высказывание |
|
|
высказывание |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x A B |
A C |
x A B x A C |
x A |
x B |
|
x A |
x C |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
высказыв. |
|
|
высказыв. |
|
||||
по закнону дистрибутивности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
над высказываниями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
def |
|
|
|
|
|
|||
|
|
|
|
|
|
x A x B x C |
|
|
x A x B C |
x A B C , т.е. |
|||||||||||||||||||||
A |
B |
A |
C |
A |
B |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Так как A |
B |
C |
A |
|
B |
|
|
|
A |
C и |
A |
B C |
A |
B A |
C , |
значит |
|||||||||||||
A |
B |
C |
A |
B |
A |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Основные законы алгебры множеств можно использовать для доказательства |
|||||||||||||||||||||||||||||
других тождеств. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
П р и м е р 7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Докажите равенство A |
A |
B |
|
A |
|
B . |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
9д |
|
|
9б |
|
|
|
|
|
|
|
|
|
||||
|
|
A B |
|
|
A B |
A |
B |
|
B |
|
A |
|
U A , что и требовалось доказать. |
|
|
|
|||||||||||||||
Формула включений и исключений
После определения операций и основных законов над множествами возникает вопрос относительно числа элементов полученных множеств.
Пусть дано конечное не пустое множество А, т.е. А Ø, состоящее из n элементов. Закрепим за каждым элементом множества А соответствующий номер 1, 2, 3, …, n. Тогда элементы множества А предстанут в занумерованном виде: a1 , a2 , a3 , , an , где номер
последнего элемента и означает число элементов множества А. Значит число n, соответствующее количеству элементов множества А 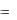 a1 , a2 , a3 , , an , будет
a1 , a2 , a3 , , an , будет
8
количественной характеристикой данного множества. Число элементов конечного множества А будем обозначать N A . Число элементов пустого множества Ø равно нулю, т.е. N A 0 .
0 .
Пусть существуют множества А и В, количество элементов которых N A и N В ,
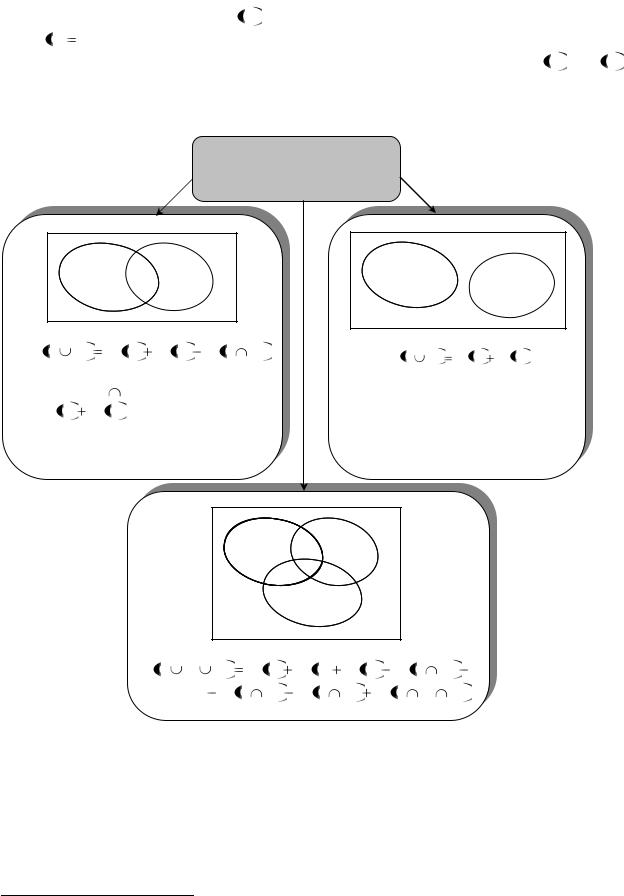
тогда общее количество элементов А и В вычисляет формула, называемая формулой включений и исключений2 (ее можно обобщить на три и более множества), которая позволяет решать многие задачи теории множеств (см. Рисунок 4).
Формула включений и исключений
|
U |
|
U |
A |
B |
A |
B |
|
|
N A |
B |
N A N B N A |
B |
N A B N A N B |
|
|
|
|
|
Так как A |
B входит в сумму |
|
Так как множества А и В не |
|
N A |
N B дважды, поэтому |
|
пересекаются, то общая часть |
|
один раз общую часть |
|
у них отсутствует и ее |
||
необходимо вычесть. |
|
вычетать не надо. |
||
|
U |
A |
B |
|
|
|
С |
N A B С N A N B N C N A B
N C N A B
N B C N A C N A B C
Рисунок 4. Формула включений и исключений.
П р и м е р 7 .
Из 16 студентов группы, изучающих английский или китайский язык, 11 – изучают китайский. Сколько студентов изучают оба языка, если английский язык изучают 9 из них?
Р е ш е н и е .
Что дано?
Даны два множества:
2 Впервые формулу включений и исключений опубликовал португальский математик Даниэль да Сильва в 1854 года. Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи о встречах.
9
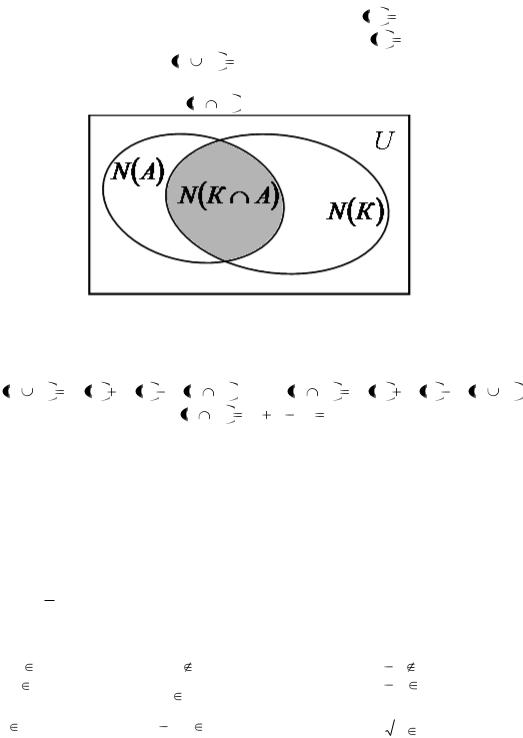
К – студенты, изучающие китайский язык, которых N К |
11. |
|
А – студенты, изучающие английский язык, которых N А |
9 . |
|
Всего студентов 16, т.е. N К |
А 16 . |
|
Что нужно сделать? Узнать сколько студентов изучают оба языка одновременно |
||
(и китайский, и английский), т.е. N К |
А (см. рисунок 5). |
|
Рисунок 5
Значит, количество студентов в группе изучающих оба языка можно вычислить по формуле включений и исключений:
N К А N К N А N К А , т.е. N К А N К N А N К А
N К А 11 9 16 4 .
О т в е т . 4 человека изучают оба языка: китайский и английский язык.
Упражнения для выполнения
1)Приведите примеры множеств из обычной жизни. Какие множества, из приведенных примеров, является конечными, а какие нет. Поясните свой ответ.
2)Запишите, используя символы: а) число 12 – натуральное;
б) число – 6 – не является натуральным; в) число 0 является рациональным; г) число 
 2 - действительное.
2 - действительное.
3)Прочитайте следующие высказывания и укажите среди них верные, поясните свой ответ:
а) |
100 |
N ; |
г) |
103 |
R ; |
ж) |
3 |
N ; |
|||
б) |
5,2 |
Q ; |
д) |
4 |
N ; |
з) |
4 |
Z ; |
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
7 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
в) |
0 |
N ; |
е) |
|
|
6,7 |
R ; |
и) |
|
|
Q . |
|
|
5 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
4)Перечислите элементы следующих множеств:
а) А – множество нечетных однозначных множеств; б) В – множество натуральных чисел меньших или равных13; в) С – множество двухзначных чисел, делящихся на 5.
5)Задайте множество D, которое состоит из натуральных чисел: а) кратных 3; б) больших 40, но меньших 70;
в) не больших 13; г) четных двухзначных чисел;
д) по крайней мере равных 10.
6)Укажите характеристическое свойство элементов множества:
а) {а, е, ѐ, и, о, у, э, ю, я, ы};
10
