§ 7. Энергия в релятивистской механике

Найдем кинетическую энергию ре­лятивистской частицы. Элементарная работа силы F на малом перемещении 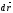равна 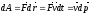(учли основной закон релятивистской динамики (18)]. Тогда

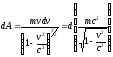
(этот результат можно проверить дифференцированием).

Приращение кинетической энергии материальной точки на элементарном перемещении равно элементарной работе на том же перемещении dT = dA. Тогда

.

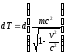Интегрируя это выражение получим

.

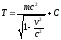Поскольку кинетическая энергия при v 0 должна обращаться в нуль, то постоянная интегрирования С= —mc². Следовательно, кинетическая энергия релятивистской частицы

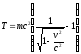. (20)

Выражение (20) при скоростях v << c переходят в классическое:

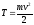, (21)

(разлагая в ряд 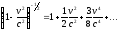, приv << c правомерно пренебречь слагаемыми второго порядка малости).

Полная энергия свободной частицы, т.е. частицы, на которую не действуют силы,

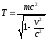. (22)

Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле. Полная энергия частицы в разных системах отсчета различна.

В случае покоящейся частицы (v = 0) из формулы (22) найдем, что

E₀ = m c² (23)

Величина, определяемая выражением (23), называется энергией покоя. Значения т и Е₀ не зависят от выбора инерциальной системы отсчета. В энергию покоя, как и в полную энергию (22), не входит энергия тела во внешнем силовом поле. В классической механике энергия покоя не учитывается, считая, что при v = 0 энергия покоящегося тела равна нулю.

Как энергия Е, так и импульс р реля­тивистской частицы имеют различные значения в разных системах отсчета. Но существует величина Е — р²с² = inv, являющаяся инвариантной (имеющей одно то же значение в разных системах отсчета):

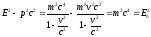. (24)

(учли формулы (19), (22) и (23)). Согласно формуле (24), получим 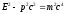, откуда связь между энергией и импульсом

или

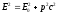. (25)

Из выражений (22), (20) и (23) следует, что полная энергия системы

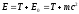, (26)

т.е. складывается из ее кинетической энергии и энергии покоя. Подставив (26) в (25), получим

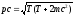, (27)

откуда следует, что при T << mc² выражение (27) переходит в ньютоновское (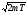), а при T >> mc² приобретает вид .

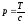Согласно формуле (23), масса тела и его энергия покоя связаны между собой. Это означает, что всякое изменение массы тела m сопровождается изменением энергии покоя Е₀, и эти изменения пропорциональны друг другу, т. е.

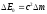. (28)

Выражение (28) носит название закона взаимосвязи массы и энергии покоя.

Чтобы охарактеризовать прочность связи и устойчивость системы каких-либо частиц (например, атомного ядра как системы из протонов и нейтронов), вводят понятие энергии связи. Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро — на протоны и нейтроны). Энергия связи системы ,

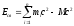где m_i — масса i-й частицы в свободном состоянии; М— масса системы. Закон взаимосвязи массы и энергии покоя (иногда говорят просто энергии) подтвержден экспериментами о выделении энергии при протекании ядерных реакций. Он широко используется для расчета энергетических эффектов при ядерных реакциях и превращениях элементарных частиц.

Выводы специальной теории относительности, как, впрочем, и любые крупные открытия, потребовали пересмотра многих установившихся и ставших привычными представлений. Так, длина тел и длительность событий не являются абсолютными величинами, а носят относительный характер, масса и энергия покоя оказались связанными друг с другом, хотя они и являются качественно различными свойствами материи.

Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи «пространство — время». Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи

Контрольные вопросы

• В чем физическая сущность механического принципа относительности?

• В чем заключается правило сложения скоростей в классической механике?

• Каковы причины возникновения специальной теории относительности?

• В чем заключаются основные постулаты специальной теории относительности?

• Зависит ли от скорости движения системы отсчета скорость тела? скорость света?

• Запишите и прокомментируйте преобразования Лоренца.

• При каких условиях они переходят в преобразования Галилея?

• Какой вывод о пространстве и времени можно сделать на основе преобразований Лоренца?

• Одновременны ли события в системе К', если в системе К они происходят в одной точке и одновременны? в системе К события разобщены, но одновременны? Обоснуйте ответ.

• Какие следствия вытекают из специальной теории относительности для размеров тел и длительности событий в разных системах отсчета? Обоснуйте ответ.

• При какой скорости движения релятивистское сокращение длины движущегося тела составит 25 %?

• В чем состоит «парадокс близнецов» и как его разрешить?

• В чем заключается релятивистский закон сложения скоростей? Как показать, что он находится в согласии с постулатами Эйнштейна?

• Как определяется интервал между событиями? Докажите, что он является инвариантом при переходе от одной инерциальной системы отсчета к другой. Какой вид имеет основной закон релятивистской динамики? Чем он отличается от основного закона ньютоновской механики?

• В чем заключается закон сохранения релятивистского импульса?

• Как выражается кинетическая энергия в релятивистской механике? При каком условии релятивистская формула для кинетической энергии переходит в классическую формулу? Сформулируйте и запишите закон взаимосвязи массы и энергии. В чем его физическая сущность? Приведите примеры его экспериментального подтверждения.

ЗАДАЧИ

1. Определите собственную длину стержня (длину, измеренную в системе, относительно которой стержень покоится), если в лабораторной системе (системе отсчета, связанной с измерительными приборами) его скорость v = 0,8 с, длина I = 1 м и угол между ним и направлением движения 30⁰

2. Собственное время жизни частицы отличается на 1,5 % от времени жизни по неподвижным часам. Определите отношение v/c

3. Тело массой 2 кг движется со скоростью 200 Мм/с в системе К', движущейся относительно системы К со скоростью 200 Мм/с. Определите: 1) скорость тела относительно системы К; 2) его массу в этой системе.

4. Воспользовавшись тем, что интервал — инвариантная величина по отношению к преобразованиям координат, определите расстояние, которое пролетел -мезом с момента рождения до распада, если время его жизни в этой системе отсчета At = 5 мкс, а собствен­ное время жизни (время, отсчитанное по часам, движущимся вместе с телом) Д = 2,2 мкс.

5. Определите скорость, при которой релятивистский импульс частицы превышает ее ньютоновский импульс в пять раз.

6. Определите скорость, полученную электроном, если он прошел ускоряющую разность потенциалов 1,2 МэВ.

7. Определите релятивистский импульс электрона, кинетическая энергия которого 1 ГэВ.