§ 9. Экстремумы функции. Необходимые условия существования экстремума

Определение 1. Точка х₀ из области определе­ния функции f называется точкой минимума этой функ­ции, если найдется такая -окрестность ]х₀-; х₀ +[ точких₀, что для всех хх₀ из этой окрестности вы­полняется неравенство

f(x)>f(x₀).

Определение 2. Точка х₀ из области определения функции f называется точкой максимума этой функции, если найдется такая -окрестность ]х -; х +[ точких₀ , что для всех хх₀ из этой окрестности выполняется неравенство

f(x)<f(x₀).

Точки минимума и максимума называются точками экстремума, а значения функции в этих точках назы­ваются экстремумами функции.

Рассмотрим график функции y = f(x), х [а; b] (рис. 6). Точки хи х₃ являются точками максимума, а х₂ и — точками минимума. Из рис. 6 видно, что

Рис 6 Рис 7

минимум в точке хбольше максимума данной функции в точке х.Это объясняется тем, что экстремум функции связан с определенной -окрестностью точки экстре­мума, а не со всей областью определения функции. По этой причине употребляется термин «локальный экстре­мум», т. е. экстремум, связанный с данным местом. Этим же объясняется и тот факт, что точки а иb не от­носятся к точкам экстремума. Для них не существуют -окрестности, принадлежащие области определения функции.

Необходимые условия существования экстремума дает теорема Ферма, которая известна по школьному курсу, поэтому мы приводим лишь ее формулировку.

Теорема Ферма. Если точка х₀ является точкой экстремума функции у = f(x) и в этой точке существует производная f (х₀), то = 0.

Эта теорема имеет простой геометрический смысл: касательная к графику функции у = f(x) в точке, удов­летворяющей условиям теоремы Ферма, параллельна оси абсцисс (рис. 7).

Напомним, что точки, в которых производная функ­ции обращается в нуль или не существует, называются критическими точками (первого рода).

Теорема Ферма дает лишь необходимое условие существования экстремума, но не достаточное.

Пример 1. Производная функ­ции f(x)=x³ в точке х₀ = 0 обра­щается в нуль, а экстремума в этой точке функция не имеет (рис. 8).

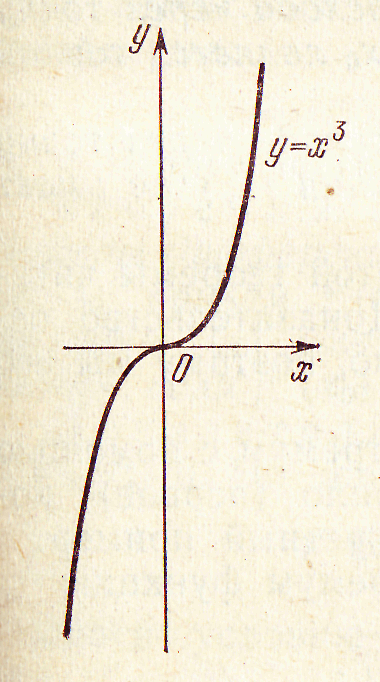
Рис 8

Можно показать, что и в тех критических точках, в которых про­изводная не существует, функция

также может иметь или не иметь экстремум.

Пример 2. Функция f(x) = |x| в точке х₀ = 0 не имеет производной (см. § 1) Однако, как видно из

рис. 3, в точке она имеет экстремум (минимум)

Пример 3. Рассмотрим функцию f(x) = (рис. 9). По графику видно, что в точке х₀ = 0

данная функция экстремума не имеет. Производная в рассматриваемой точке не существует.

Рис 9

Таким образом, экстремум функции, если он сущест­вует, может быть только в критических точках. Но это не означает, что во всякой критической точке функция имеет экстремум.

Чтобы выяснить, в каких критических точках функ­ция имеет экстремум, рассмотрим достаточные условия существования экстремума.

§ 10. Достаточные условия существования экстремума

1. Первое достаточное условие.

Теорема 1. Пусть функция y = f(x) непрерывна в точке х₀ и в ее-окрестности имеет производную, кроме, быть может, самой точке х₀. Тогда:

1) если производная f (х) при переходе через точку х₀ меняет знак с плюса на минус, то х₀ является точкой максимума;

2) если производная f (х) при переходе через точку х₀ меняет знак с минуса на плюс, то х₀ является точкой минимума;

3) если производная f'(x) при переходе через точку х₀ не меняет знак, то в точке х₀ функция f(x) не имеет экстремума.

С доказательством первой части этой теоремы чита­тель знаком по школьному курсу. Доказательство ос­тальных частей проводится аналогично, поэтому мы его не приводим.

При исследовании функции на экстремум с помощью первой производной применяют правило (первое), которое мы сформулируем, решая конкретный пример.

Пример 1. Исследовать на экстремум функцию

f (х) = (2х + 1).

Решение.

1. Находим производную данной функ­ции:

2. Находим критические точки: а) решая уравнение

получим х =1.

б) f'(x) не существует при х = 2. Следовательно, критические точки: = 1 и х= 2.

3. Методом пробных точек определяем знак произ­водной в каждом из интервалов: ]-; 1 [, ]1; 2[, ]2; +[ (рис. 10). Имеем:

при

при

при

Таким образом, = 1 — точка максимума, а = 2 — точка минимума.

Рис 10

4. Вычисляем значения данной функции в точках экстремума:

;