2. Двухкартинный комплексный чертеж и его основные свойства
Определение двухкартинного чертежа: Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинный или комплексным.
Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.
В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П1 располагают горизонтально, а вторую П2 - вертикально. П1 - горизонтальная плоскость проекций, П2- фронтальная. Плоскости бесконечны и непрозрачны.
Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.
Линия пересечения плоскостей проекций называется осью координат и обозначается x12.
Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти.
Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2 (рис.6). Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа (франц. Epure – чертеж.) или комплексным чертежом.
Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы).
Поле
точек, имеющих равные координаты (y=z)
образует плоскость П13,
которая называется нечетной
бисекторной плоскостью.
Она делит четверти I
III
пополам.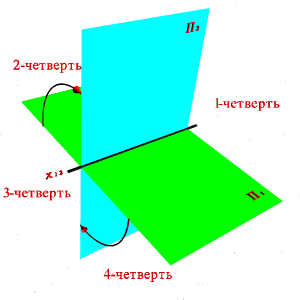
Плоскость П24, которая делит пополам II и IV четверти, называется четной биссекторной плоскостью. Координаты ее точек равны по величине, но противоположны по знаку.
На рисунке 8 представлены точки A, B, C и D, расположенные в разных четвертях пространства и их эпюр (A - в первой, B - во второй, C - в третьей и D - в четвертой четвертях)
3. Трехкартинный комплексный чертеж и его основные свойства
Трехкартинный комплексный чертеж образуется методом ортогонального проецирования на три взаимно перпендикулярные плоскости проекций: /7, _L П2 -L П3 (рис. 5.6).
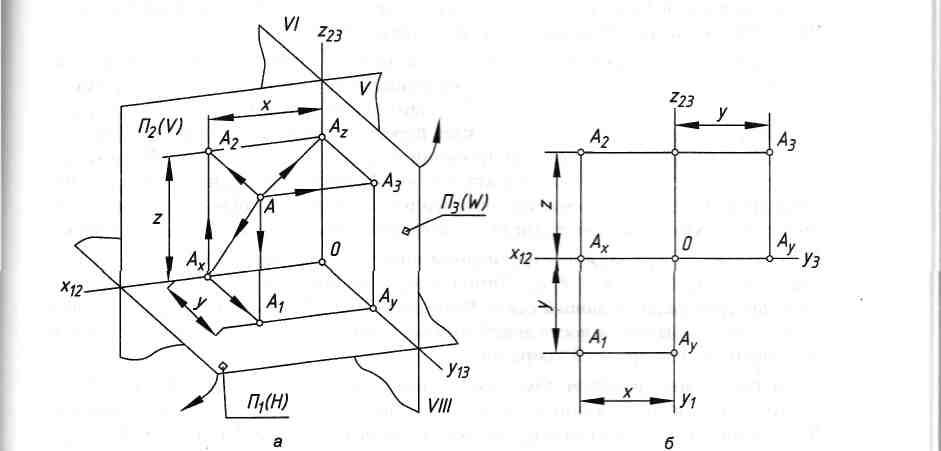
Введением плоскости fl3{W) мы разделили все пространство на восемь частей, каждая из которых называется октантом. Нумерация четвертей сохраняется за первыми четырьмя октантами, а новым октантам присваиваются номера с V по VIII, как показано на рис. 5.6, а, где октант VII не показан, так как его не видно.
Постоянная чертежа- диагональ.
Задачи 2 и 3.
4. Проецирование прямой
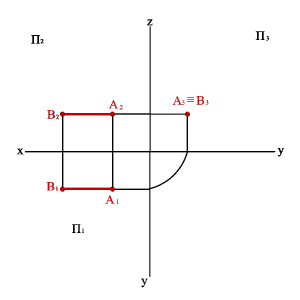
Прямая может иметь свои проекции в виде двух прямых или в виде точки и прямой.
Виды прямых:
Общего положения
Горизонталь
Фронталь
Профильная прямая
Гориз. Проец.
Фронт. Проец.
Проф. Проец.
Определения:
Прямая не параллельная ни одной плоскости проекций называется прямой общего положения
Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями
Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями
Прямые параллельные профильной плоскости проекций называются профильными