Плотность распределения отклонений

Найдем вероятности попадания в разряды по формуле

Получим

;

Умножив эти вероятности на количество выстрелов n=500, получим теоретические частоты попадания в каждый из интервалов. Сопоставим теоретические и статистические частоты

i	-4,-3	-3,-2	-2,-1	-1,0	0,1	1,2	2,3	3,4
mi	6	25	72	133	120	88	46	10
pin	7,2	26,4	71,4	121.9	130,2	91,45	38,8	12,65

Рассчитаем величину критерия

Число степеней свободы  = 8 – 3 = 5. По таблице находим:

для ²=3,00 р=0,7;

для ²=4,35 р=0,5;

Интерполяцией находим

.

Эта вероятность малой не является, поэтому гипотезу о том, что разброс результатов подчиняется нормальному закону, можно считать правдоподобной.

15. В ряде случаев необходимо оценить доверительный интервал генеральной дисперсии D_x или _х² (теоретической величины) по выборочной дисперсии. Доказано, что если результаты измерения случайной величины Х (x₁, , x_n) распределены по нормальному закону, то сумма

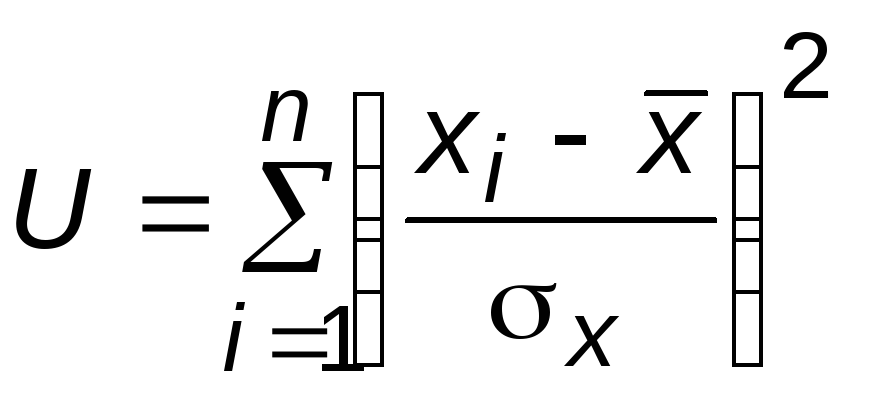
имеет распределение ² с =n-1 степенями свободы.

Сделаем некоторые преобразования.

.

Отсюда искомая величина

.

В таблицах распределения ² для ряда уровней значимости  и числа степеней свободы  приводятся критические значения параметра ²_кр. Эти значения показывают, что случайная величина U, распределенная по закону ², с вероятностью  будет больше табличного значения ²_кр.

Предположим, что было произведено 10 измерений. Число степеней свободы =10-1=9. Из таблицы находим, что для =0,95 ²_кр=3,325; для =0,05 ²_кр=16,92. Таким образом, с вероятностью 95% величина U>3,325; c вероятностью 5% U>16,92. Отсюда с вероятностью 90% величина U находится в интервале 3,325<U<16,92. Поэтому с вероятностью 90%

.

При измерении одних и тех же величин различными способами или в различные периоды времени результаты, как правило, несколько отличаются друг от друга. Если исходить из того, что каждый результат может быть отягощен некоторой ошибкой, абсолютная величина и знак которой неизвестны, то при сопоставлении результатов возникает неопределенность в оценке: соответствует ли наблюдаемое между ними различие различию между измеряемыми параметрами или же мы наблюдаем две реализации одной случайной величины, а видимое различие связано только со случайными колебаниями неконтролируемых параметров. Эта неопределенность проясняется при решении двух взаимосвязанных вопросов: значимо ли различается воспроизводимость результатов (другими словами, равноточны ли измерения) в разных сериях опытов и значимо ли различаются средние значения результатов в сериях?

Вопрос о равноточности двух серий измерений решается путем сопоставления дисперсий результатов измерений в этих сериях. Мерой оценки статистически значимого различия дисперсий является критерий Фишера

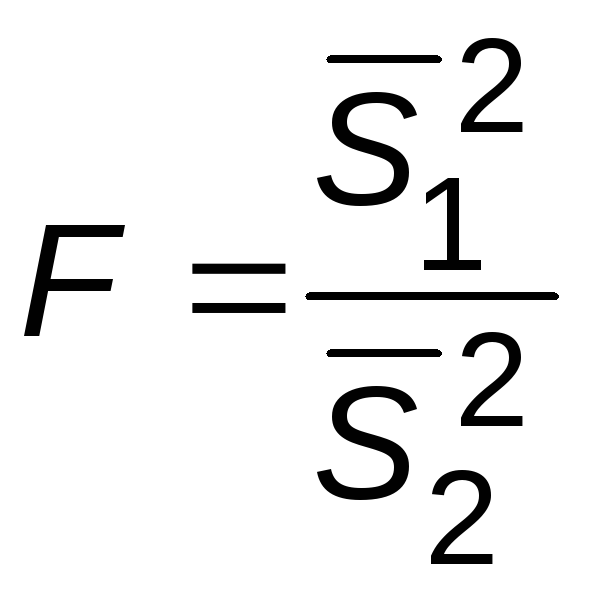, (8.7)

где - наибольшая дисперсия,.

Рассчитанное по этой формуле значение критерия сравнивают с критическим , величина которого для разных уровней значимости  и степеней свободы ₁=n₁-1 и ₂=n₂-1 приводятся в соответствующих таблицах. Здесь n₁ и n₂ - количество параллельных измерений в сериях опытов соответственно с результатами, имеющими наибольшую и наименьшую дисперсии.

При F>F_кр c доверительной вероятностью =1- можно считать, что дисперсии в первой и второй сериях опытов статистически неодинаковы, воспроизводимость опытов во второй серии выше (в этой серии разброс данных относительно среднего значимо меньше). При F<F_кр данные измерений не дают основания считать, что разброс значений во второй серии меньше, чем в первой.

Если дисперсии двух серий опытов не отличаются значимо друг от друга, то определить, есть ли статистически значимая разница в результатах серий, можно с помощью t-распределения Стьюдента. Для этого вычисляют среднее взвешенное двух дисперсий

(8.8)

и параметр

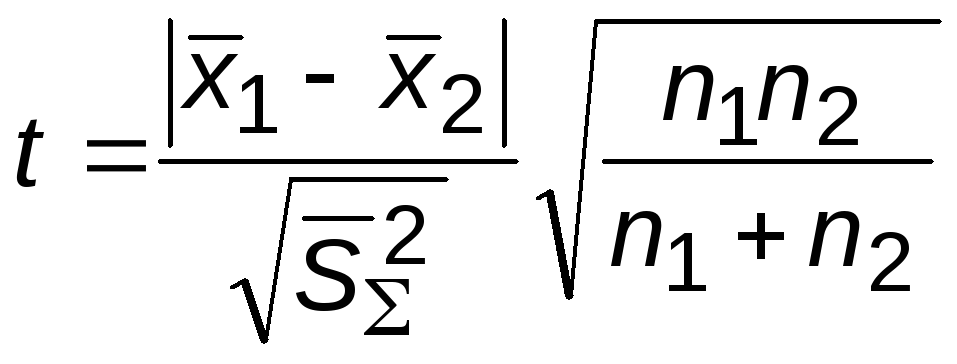. (8.9)

Далее по соответствующей таблице для числа степеней свободы =n₁+n₂-2 и уровня значимости  определяют критическое значение t_кр. Если t<t_кр, то принимают, что иявляются оценками одного математического ожидания, т.е. предполагается, что наблюдаемое различие между этими величинами статистически незначимо. Приt>t_кр с вероятностью ошибки  считают, что величины истатистически неодинаковы.

В тех случаях, когда средние значения исследуемой величины Х статистически неразличимы, можно объединить обе серии опытов, рассматривая n₁+n₂ результатов как данные одной серии. Суммарное среднее арифметическое будет равно

, (8.10)

суммарная дисперсия

. (8.11)

Частным случаем является сравнение среднего арифметического с некоторой постоянной величиной. Такая задача встречается, например, когда некоторую величину, вычисленную теоретически или заданную нормативными характеристиками, необходимо проверить экспериментально. В этом случае имеется только одно среднее и одна дисперсия.

Для сравнения полученного результата с заданной величиной а вычисляют параметр

. (8.12)

Далее по таблице для принятого уровня значимости  и числа степеней свободы =n-1 определяют значение критерия t_кр. При t > t_кр с вероятностью ошибки  можно считать, что экспериментальные данные не соответствуют нормативным или теоретическим величинам. В противном случае принимается, что наблюдаемое в опытах различие между средним значением и величиной а статистически несущественно.

При неравноточных измерениях, когда F > F_кр, при n₁=n₂=n проверку однородности результатов в двух сериях опытов можно осуществить лишь приближенно. В этом случае вычисляют параметр

. (8.13)

Для выбора критического значения t_кр число степеней свободы  рассчитывают по формуле

, (8.14)

где

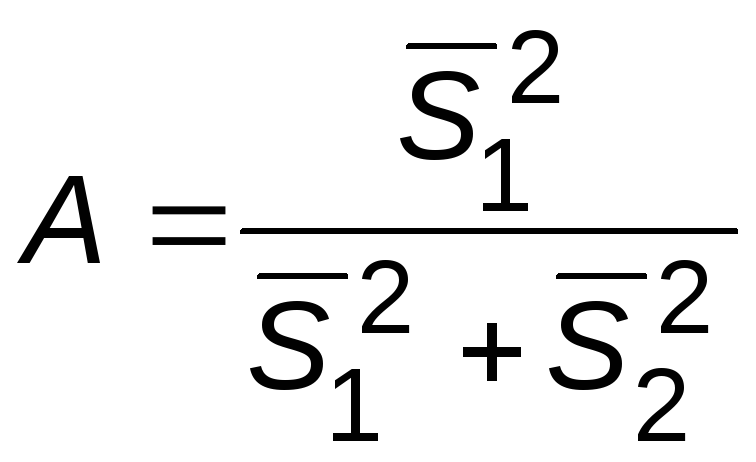. (8.15)

При t > t_кр результаты признаются статистически различимыми, в противном случае считается, что различие между ними незначимо.

Для оценки однородности дисперсий k серий опытов с числом степенней свободы ₁, ₂, …, _k применяется критерий Бартлета:

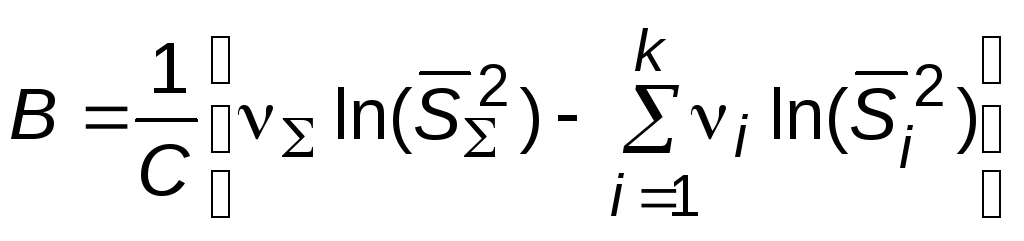, (8.16)

где средневзвешенная дисперсия определяется выражением

, (8.17)

суммарное число степеней свободы

, (8.18)

а параметр С рассчитывается по формуле:

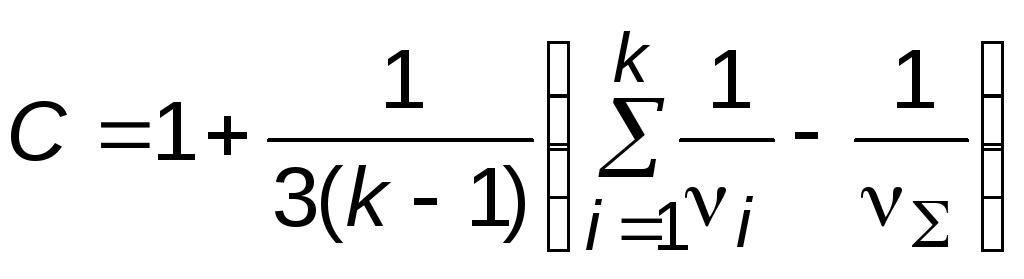. (8.19)

Величина В распределена как ² с k-1 степенями свободы. Значение ² определяется из соответствующей таблицы по уровню значимости  и числу степеней свободы =k-1.

Если найденное значение критерия В > ², то нельзя считать, что измерения равноточны во всех точках. При В < ² измерения признаются равноточными.

Если число степеней свободы для всех выборок одинаково, то есть если в каждой точке проведено одинаковое количество измерений, то для сравнения дисперсий используется более точный критерий Кохрена:

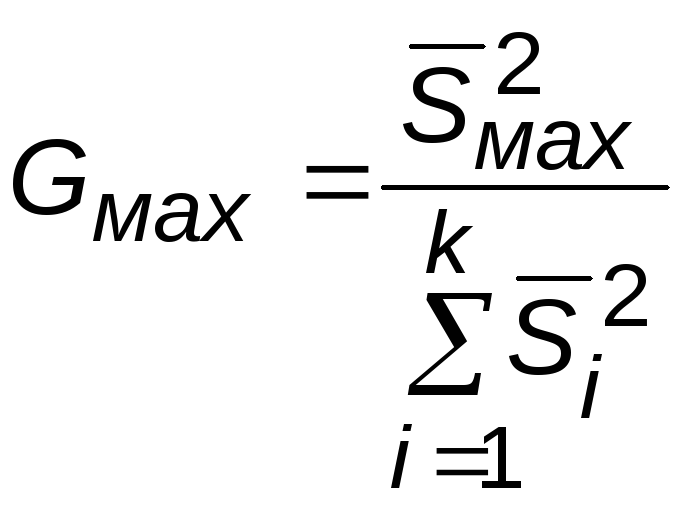. (8.20)

Здесь - максимальное значение дисперсии из дисперсий всех серий опытов. Для сравнения с вычисленным значениемG_мах по соответствующей таблице для уровня значимости , числа степеней свободы =n-1 и количества серий опытов k находится значение G_кр. Если G_мах > G_кр, то с вероятностью ошибки  принимается, что дисперсия значимо отличается от среднего значения остальных дисперсий. ПриG_мах < G_кр можно считать, что все дисперсии однородны, разброс результатов во всех точках относительно средних значений имеет один порядок, измерения во всех точках равноточны.

РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА :Распределение Стьюдента широко используется для решения многих практических задач. В первую очередь с помощью его определяется доверительный интервал случайной величины. Допустим, что были проведены n независимых измерений случайной величины Х, в результате чего получены значения х₁, х₂, ...,х_i, х_n. По этим данным, используя формулы (3.17) и (3.21) рассчитываются среднее арифметическое и выборочное среднее квадратичное отклонение. Затем по числу степеней свободы=n-1 и выбранному значению уровня значимости =1- по таблице распределения Стьюдента определяется параметр t. Так как отклонение истинного значения (математического ожидания) случайной величины m_x от среднего арифметического может быть как положительным, так и отрицательным, то в этом случае необходимо пользоваться двухсторонним критерием. Если в таблице указан односторонний критерий, то значение параметраt надо взять из таблицы для уровня значимости .

Обозначая ожидаемую величину ошибки как , из (8.2) получим

, (8.3)

откуда найдем интервал, внутри которого с доверительной вероятностью  находится истинное значение случайной величины:

. (8.4)

Для относительной характеристики погрешности определения истинного значения m_x вычисляют коэффициент вариации:

. (8.5)

Распределение Стьюдента можно использовать для отсева промахов при обработке результатов экспериментов. Грубые промахи могут появиться вследствие ошибок экспериментатора, выхода из строя измерительной аппаратуры, нарушения режима установки и т.д. Признаком ошибок такого рода является несоответствие наблюдаемых значений с физической сущностью исследуемого процесса (несоответствие полученных характеристик агрегатному состоянию вещества, нарушение законов сохранения массы, энергии, количества движения и т.д.) или значительное отклонение данных от их среднего значения. При усреднении экспериментальных данных грубые промахи могут существенно исказить конечный результат, поэтому они должны быть исключены из совокупности обрабатываемых значений. С другой стороны, если будем отбрасывать значения, которые в действительности имели место и заметно отличаются от среднего только в силу случайных колебаний, то также внесем погрешность в расчет окончательного значения.

.

Для отбраковки грубых промахов t-распределение преобразуется в r-распределение. Параметром этого распределения является величина

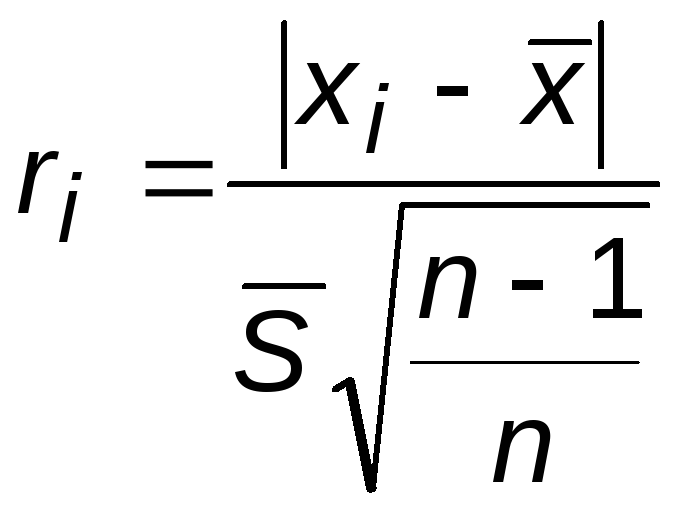. (8.6)

Если с заданной степенью доверительной вероятности =1- величина r_i попадает в доверительный интервал, то нет основания считать величину x_i грубым промахом и ее следует оставить в ряду результатов. В противном случае с вероятностью b можно признать, что величина x_i попала в этот ряд из-за грубой ошибки и ее следует исключить. Вероятность ошибки исключения равна .