
Техмех
.pdf
1.Понятие о числе степеней свободы, классификация конструкций в зависимости от числа степеней свободы. 2
2.Определение числа степеней свободы в рамах и фермах. 3-4
3.Способы образования геометрически неизменяемых систем. 5-6
4.Понятие о мгновенно изменяемых системах, способы проверки на мгновенную изменяемость. 7
5.Кинематический анализ 3х шарнирных рам и арок (с затяжкой и без), многопролетных балок и рам, понятие и поэтажных схемах. 8
6.Типы опор и возникающие в них реакции. 9-10
7.Формула Куравского, построение эпюры Q по эпюре М, эпюры N по эпюре Q. 11
8.Основные правила построения в статически определимых системах. 12
9.Принципы расчёта консольных и простых рам, определение опорных реакций, построение эпюр, проверка их правильности. 13-17
10.Особенности расчёта трёхшарнирных рам с затяжкой и без. 18-19
11.Особенности расчёта трёхшарнирных арок с затяжкой и без. 20-22
12.Особенности расчёта многопролётных балок и рам. 23-24
13)Методы определения усилий в фермах 25
14)Основные свойства статически определимых систем 26
15)Понятие об обобщённых силах и обобщённых перемещениях, возможных и действительных перемещениях, возможной и действительной работе. 27
16)Теорема Клайперона 28
17.Обобщенный закон Гука 29-30
18.Работа внутренних сил, понятие о потенциальной энергии деформации. 31-32
19Потенциальная энергия изгиба, растяжения-сжатия, сдвига. 33-34
20Принцип возможных перемещений 35-37
23.Теорема о взаимности работ (теорема Бетти) 38
24.Теорема о взаимности перемещений (Максвелла) 39
25.теорема Релея о взаимности реакций. 40
26.теорема Гвоздева о взаимности перемещений и реакций. 41
27.Определение перемещений от нагрузки. Формула Мора. 42
28.Определение перемещений от температурного воздействия и от смещения. 43-44
29.Правило Верещагина. Формула перемножения трапеций, формула Симпсона. 45-46
31.Свойства статически неопределимых систем. 47
32.Определение степени статической неопределимости, принципы выбора основной системы метода сил. 48
33.Канонические уравнения метода сил, их физический смысл. 49
34.Вычисление коэффициентов канонических уравнений, их физический смысл, проверка правильности найденных коэффициентов. 50-51
1
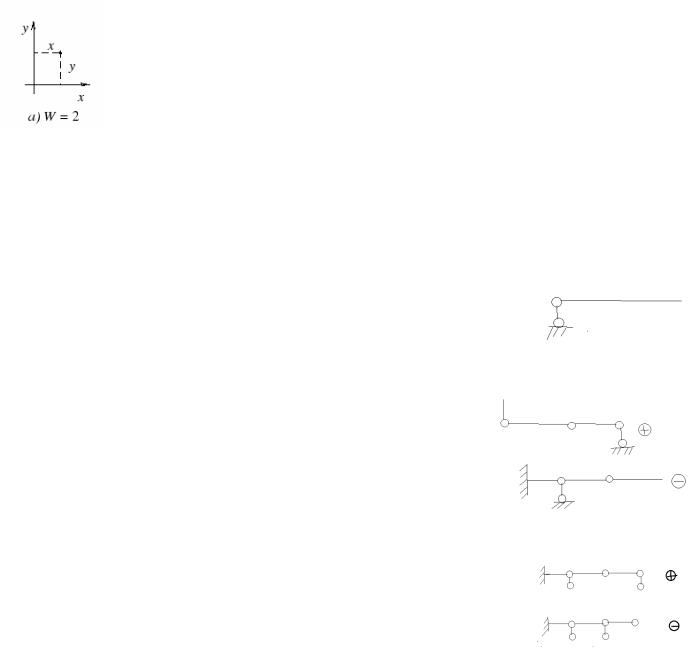
1.Понятие о числе степеней свободы, классификация конструкций в зависимости от числа степеней свободы.
Число степеней свободы плоской системы W– это число независимых геометрических параметров,определяющих положение конструкции на плоскости без учета деформации конструкции.
Изменяемая сист: перемещения ее точек возможны без деформации
конструкции;
Неизменяемая сист: ……….. только вследствие деф. констр.;
Мгновенно изм-ая сист: возможно возникновение бесконечно малых пеермещений без деформации элементов.
Классификация
1)W>0
Изменяемая система, которой не хватает связей (нельзя рассчитать-«-»)
2)W=0
Сист. Имеет дост. число связей, чтобы быть геом-и неизменяемой. Важнго, чтобы эти связи были правильно
поставлены,то естьтакая система требует дальнейшего анализа геом структуры.
3)W<0
Сист имеет много связей (лишних) , но при этом она может быть как геом-и изменяемой,так и геом-и неизменяемой, то естьтакая система требует анализа геом структуры, которая построена на принципах образования геом-и неизменяемых систем.
2
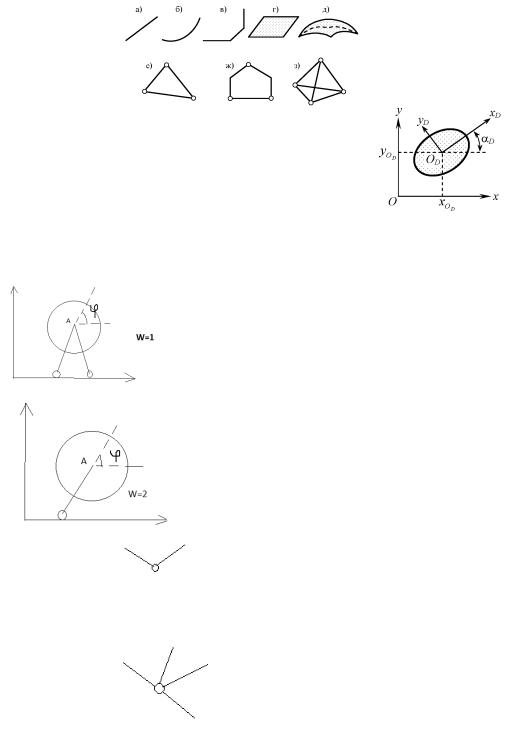
2.Определение числа степеней свободыв рамахи фермах.
Диск-любая неизменяемая система.
|
В плоскости диск обладает |
тремя степенями свободы– это |
координаты X,Y и угол ά |
(альфа). |
|
Шарнир отнимает у системы 2 |
степени свободы. |
Шарнир отнимает у диска 2 степени свободы.
Стерженьотнимает одну степень свободы.
Простой шарнир соединяет 2 диска.
Если в шарнир соед-ся n дисков , то он наз. Кратным и равносилен (n-1) шарниру.
Если соед-ся шарнирно в узле n дисков, то получается(n-1) простой шарнир.
Пустьимеется С0 опорных стержней.(заделка эквивалентна 3-м опорным стержням).
3

-Препятствует углу поворота.
Если 3 диска, то W=3D
Каждый шарнир отнимает 2 ст.св.,след-о «-2Ш» Каждый опорный стерженьотнимает 1 ст.св.,слеж-о «-С0»
W=3Д-2Ш-С0 -универсальная формула Чебушева для определения ст.св. любой плоской сист.(ДЛЯ РАМ!)
У-число узлов
С-число стержней
С0-число опорных стержней
W=3Д+2У-2Ш-С0 -только для шарнирно-стержневых сист,тк как нет жестких узлов(ДЛЯ ФЕРМ!)
4
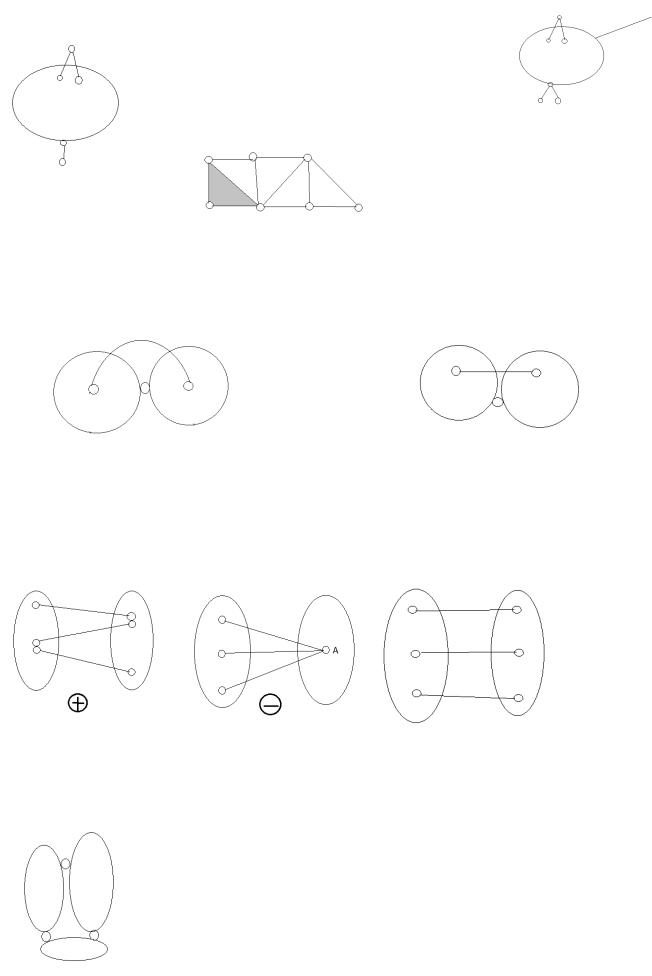
3.Способыобразования геометрически неизменяемыхсистем.
1)Диада 2-х стержневых систем. Присоединение диады,то есть 2-х стержневого звена не меняет геом изменяемости/неизм-ти сист.
-упадет.
-треугольная |
неизменяемая система. |
2) 2 диска можно соединитьнеизменяемо шарниром и стержнем, ось которого не проходит через этот шарнир.
Изменяемая |
Неизменяемая |
3) 2 диска можно соединить неизменяемо с помощью 3-х стержней, не параллельных и не пересекающихся в данной точке.
4) 3 диска можно соед неизм-о с помощью 3-х шарниров, не лежащих на одной прямой.
5
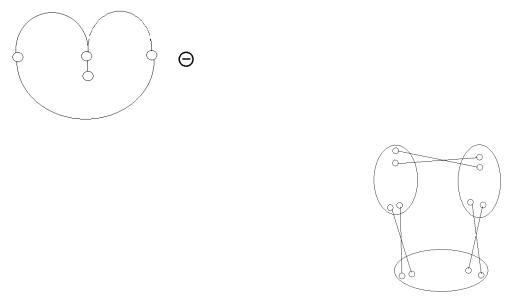
5) Шарнир-точка пересечения стержней. |
|
3 диска можно соед попарно 3-мя парами |
стержней, |
каждая из которых создает фиктивные шарниры, |
не лежащие |
на одной прямой. |
|
6
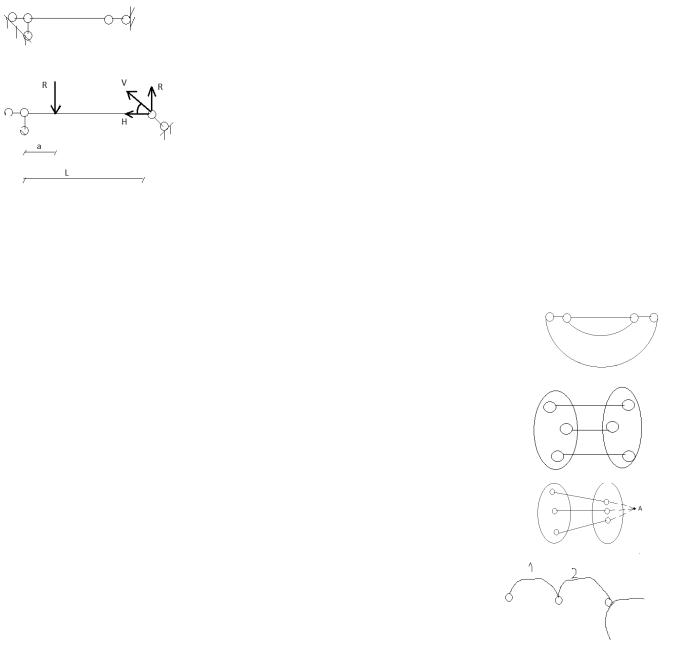
4.Понятие о мгновенно изменяемыхсистемах, способыпроверки на мгновенную изменяемость.
Мгновенно изменяемой системойназ. Система,если она допускает бесконечно малые перемещения без деформации элементов,после чего она становится неизменяемой.
R=V*sin(альфа)
ΣMa=P*a-V*sin(a)*L=0
Lim V(при альфа стремится к нулю)=P*a/0 «стремится» к бесконечности.
В мгновенно изменяемых системах возникают бесконечно большие или неопределенные усилия,поэтому проектирование таких конструкций невозможно.
Принципы мгновенной изменяемости:
1)Соединение 2-х дисков с помощью шарнира и стержня, оськоторого проходит через этот шарнир.
2)Соед-е 2-х дисков 3-мя параллельными стержнями разной длины.
3)Соед 2-х дисков 3-мя стержнями, оси которых пересекаются в одной точке.
4)Соед 3-х дисков с помощью 3-х шарниров,лежащих на одной прямой.
7
5.Кинематический анализ 3хшарнирныхрам и арок (с затяжкой и без), многопролетныхбалок и рам, понятие и поэтажных схемах.
Кинематический анализ сооружений начинается с определения числа степеней свободы. W= 2D-2Ш-С0 Формула Чебушева для любой плоск системы
,гдеDчисло дисков
Ш- число простых шарниров ( соед. Только 2 диска), если шарнир соед. N дисков, о такой шарнир называется кратным и он равносилен n-1 простому шарниру
С0количество опорных стержней(Заделка эквивалентна 3м опорным стержням.
Если система шарнирно-стержневая, то
W=2У-С-С0
,где С0число опорных стержней С-число стержней У -число узлов.
Система называется мгновенно изменяемой, если допускает б.м. перемещения без деформации элементов, после чего она становится неизменяемой.
В мгновенно изменяемых системах возник б.б. или неопред. усилия, поэтому проектировать такие конструкции мы не можем.
Признаки мгновенной изменяемости:
1)соединение 2х дисков с помощью шарнира и стержня, ось которого проходит через этот шарнир.
2)соединение 2х дисков 3мя параллельными стержнями разной длины
3)соединение 2х дисков 3мя стержнями, оси которых пересекаются в одной точке
4)Соединение 3х дисков с помощью 3х шарниров, лежащих на 1й прямой.
8

6.Типыопор и возникающие в нихреакции.
1. Защемление, или заделка (рис. 4.7, а). Защемленный (или заделанный) конец бруса не может ни смещаться поступательно, ни поворачиваться. Следовательно, число степеней свободы бруса с защемленным концом равно нулю. В опоре могут возникать:
вертикальная реакция (сила R — рис. 4.7, а), препятствующая вертикальному смещению конца бруса; горизонтальная реакция (сила Н), исключающая возможность его
горизонтального смещения 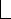

 и реактивный момент препятствующий повороту. Таким образом, закрепление бруса с помощью заделки накладывает на него три связи и обеспечивает его неподвижность.
и реактивный момент препятствующий повороту. Таким образом, закрепление бруса с помощью заделки накладывает на него три связи и обеспечивает его неподвижность.
2.Шарнирно неподвижная опора (рис. 4.7, б). Поперечное сечение бруса, проходящее через шарнирно неподвижную опору, не может смещаться поступательно. В опоре возникает реактивная сила, проходящая через центр шарнира. Ее составляющими являются вертикальная сила R, препятствующая вертикальному смещению, и горизонтальная сила Н, исключающая горизонтальное смещение закрепленного сечения бруса. Опора не препятствует повороту бруса относительно центра шарнира, и, следовательно, брус, закрепленный при помощи одной такой опоры, имеет одну степень свободы. Закрепление бруса с помощью шарнирно неподвижной опоры, накладывает на него две связи.
3.Шарнирно подвижная опора (рис. 4.7, в). Поперечное сечение бруса, проходящее через
шарнирно подвижную опору, может смещаться параллельно опорной плоскости 

 и поворачиваться, но оно не может смещаться перпендикулярно к опорной плоскости. В опоре возникает только одна реакция в виде силы R, перпендикулярной к опорной плоскости. Закрепление бруса с помощью такой опоры накладывает на него одну связь.
и поворачиваться, но оно не может смещаться перпендикулярно к опорной плоскости. В опоре возникает только одна реакция в виде силы R, перпендикулярной к опорной плоскости. Закрепление бруса с помощью такой опоры накладывает на него одну связь.
Рассмотренные типы опор принято также изображать с помощью стерженьков.
Шарнирно подвижную опору изображают в виде стерженька, имеющего по концам шарниры (рис. 5.7, а). Нижний шарнир неподвижен, а верхний может смещаться лишь по прямой линии, перпендикулярной к оси стерженька.
9
Рис. 5.7
Это соответствует тем условиям закрепления, которые обеспечивает шарнирно подвижная опора (см. рис. 4.7, в). Опорная реакция действует только вдоль оси стерженька. Собственные деформации его при расчетах не учитываются, т. е. стерженек считается бесконечно жестким.
Шарнирно неподвижную опору изображают с помощью двух стерженьков с шарнирами по концам (рис. 5.7, б). Верхний шарнир является общим для обоих стерженьков. Направления стерженьков могут быть произвольными. Они, однако, не должны быть расположены на одной прямой.
Заделку (защемление) можно изображать с помощью трех стерженьков с шарнирами по концам, как показано на рис. 5.7, в.
Число стерженьков в схематическом изображении опоры равно числу составляющих опорной реакции и числу связей, накладываемых этой опорой на конструкцию.
10
