
Техмех
.pdf
18 вопрос
Работа внутренних сил, понятие о потенциальной энергии деформации.
Сплошное тело не имеет частиц. Его сплошность обуславливается внутренними связями, распределенными сплошным образом. Рассечем тело некоторой поверхности на две части. Согласно аксиоме связей, можно действие связей, нарушенных при рассекании, заменить их реакциями. Эти силы и будут внутренними силами. Из принципа отвердевания следует, что условия равновесия в данном случае будут теми же, что и для тела абсолютно твердого. Составляя уравнение статики для оставшейся части, обнаруживаем внутренние силы.
F2 |
Fn |
F |
|
|
|
Пусть на тело действуют |
|
|
|
|
|
система уравновешивающих |
|||
|
|
2 |
|
|
R i -внутренние |
||
|
|
|
|
|
|||
|
|
|
|
|
силы |
друг друга сил: F1...,Fn.Рассечем |
|
|
F1 |
|
|
F1 |
|||
|
|
|
тело на две части и рассмотрим |
||||
|
|
|
|
|
|
||
равновесие левой части. |
Тогда условия равновесия будут выглядеть |
||||||
|
|
|
i |
|
|
i |
|
|
1) Fл R |
0 |
|
2) m0 Fл |
m0 R |
0 |
|
1 
max
где Fл и m0 Fл - соответственно главный вектор и главный
момент относительно некоторой точки внешних сил, приложенных к
левой части;
R i m0 R i - главный вектор и главный момент внутренних сил,
действующих в данном сечении.
|
3 |
|
|
экв |
Потенциальная энергия деформации может быть |
|||||
|
|
|||||||||
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
представлена в виде суммы двух слагаемых: потенциальной |
|||
|
|
|
|
|
|
|
|
|
|
|
1 3 |
экв |
энергии изменения объема и потенциальной энергии |
||||||||
2 |
|
|
max |
|
|
формоизменения. Последняя величина может служить |
||||
|
|
2 |
||||||||
критерием перехода в пластическое состояние.
31
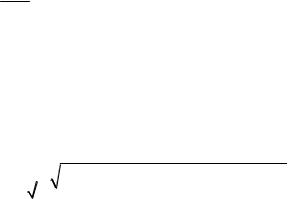
Для сложного напряженного состояния потенциальная энергия формоизменения выражается (если отнести энергию к единице объема):
Uоф 1 [( 1 2)2 ( 2 3)2 ( 3 1)2] 6Е
Для одноосного напряженного состояния |
Uоф |
|
1 |
|
экв2 |
|
|||||
|
|
|
3Е |
|
|
Т.к. оба напряженных состояния равноопасны, то обе величины можно приравнять и в результате:
|
|
1 |
|
|
|
||
экв |
|
|
|
( 1 2)2 ( 2 3)2 ( 3 1)2 |
|||
|
|
|
|||||
2 |
|||||||
|
|
|
|
||||
32
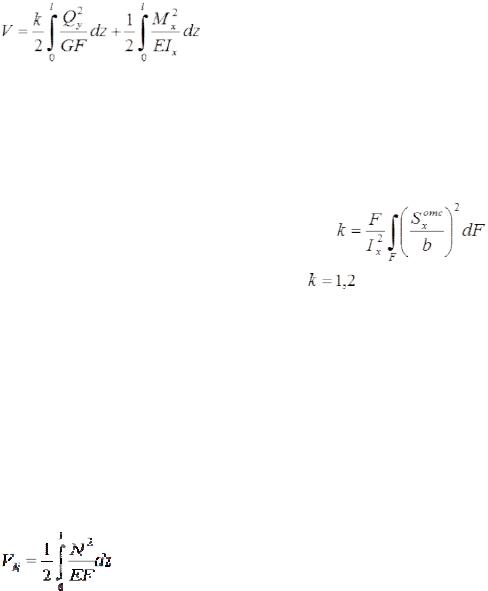
19 вопрос
Потенциальная энергия изгиба, растяжения-сжатия, сдвига.
Потенциальная энергия деформации при поперечном изгибе балки определяется по формуле:
,
Потенциальная энергия деформации при поперечном изгибе складывается
изпотенциальной энергии сдвига (первый интеграл) и энергии чистого изгиба (второй интеграл).
Значение безразмерного коэффициента k зависит от формы поперечного
сечения балки и вычисляется по формуле |
. Например, для |
прямоугольного поперечного сечения |
. |
Для большинства типов балок потенциальной энергии сдвига при изгибе в
формуле значительно меньше энергии чистого изгиба, поэтому при определениипотенциальной энергии деформации при изгибе влиянием сдвига пренебрегают.
Потенциальная энергия деформации при растяжении (сжатии) определяется по формуле:
Энергия – это способность совершать работу. При растяжении
(сжатии) внешние силысовершают работу на перемещениях, которые получают точки их приложения в результате деформирования стержня. Вследствие работы, внутри тела накапливаетсяпотенциальная энергия (V). (1 ДЖ = 1 Н·м). Один джоуль – энергия среднего яблока, находящегося на кухонном столе.
33
Энергию можно запасти, например, в пружине, однако, как заметил Гук, поведение пружины является прототипом поведения деформированного твердого тела при воздействии на него внешней нагрузки.
Таким образом, любое деформированное упругое тело является как бы аккумулятором энергии, и потенциальная энергия деформации – это запасенная энергия, которую получило тело при деформации, и которая может быть превращена в работу.
34
20 вопрос
Принципвозможных перемещений
Рассмотрим возможные перемещения точки М на стержне, прикрепленном к неподвижной поверхности шарниром О. Конечно, стержень позволяет точке двигаться по сферической поверхности в любом направлении и на любое расстояние. Все эти перемещения возможны. Возможно, кстати, перемещение и вниз. Но такое перемещение не стоит называть возможным, потому что нарушается связь, стержень. Кроме того, возможным перемещением будем называть только малое перемещение, настолько малую часть траектории, что ее можно заменить прямой, отрезком касательной.
Возможным перемещением точки материальной системы будем называть ее бесконечно малое перемещение, допускаемое связями этой системы.
Возможные перемещения точек системы должны удовлетворять двум условиям:
1)они должны быть бесконечно малыми, так как при конечных перемещениях система перейдет в другое положение, где условия равновесия могут быть другими;
2)они должны быть такими, чтобы при этом все наложенные на систему связи сохранялись, так как иначе мы изменим, вид рассматриваемой механической системы (система станет другой).
Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Так, рассмотренный выше шарик на плоскости (или на поверхности), если его считать материальной точкой, имеет 2 степени свободы. У кривошипно-шатунного механизма будет, очевидно, одна степень свободы.
У свободной материальной точки – 3 степени свободы (независимыми будут 3 перемещения вдоль взаимно перпендикулярных осей). Свободное твердое тело имеет 6 степеней свободы (независимыми перемещениями будут: 3 поступательных перемещения вдоль осей координат и 3 вращательных вокруг этих осей).
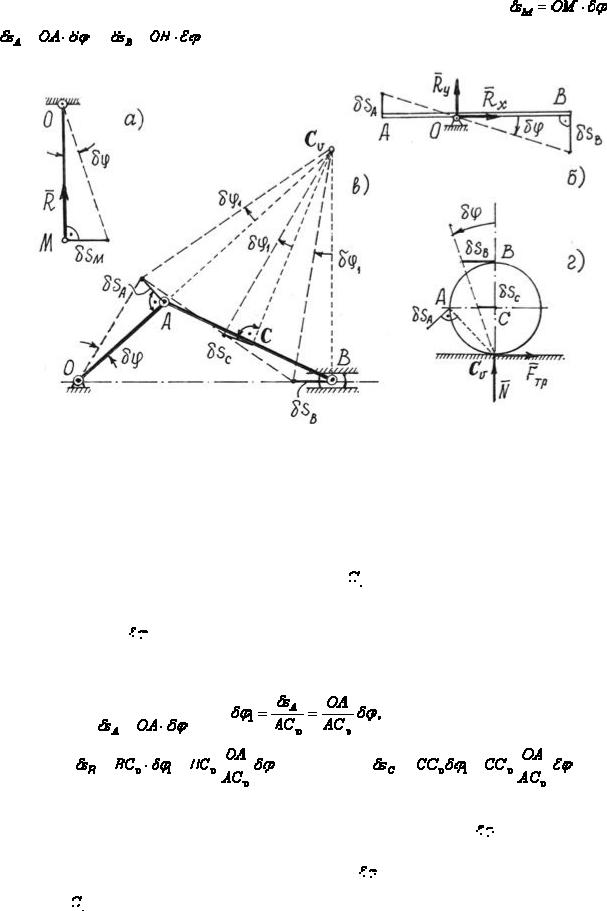
возможным перемещением всего тела, вращающегося вокруг оси,
является малый угол поворота 





 . И возможные перемещения точек его
. И возможные перемещения точек его
35
можно |
определить |
с помощью этого угла. Так, например, |
|||||||||||||||
; |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
(рис.64, а и 64, б). |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис.64
Так как направления возможных перемещений имеют направления скоростей, то перемещения точек звена АВ (рис.64, в) определяются с
помощью мгновенного центра скоростей 



 этого звена. А возможное перемещение всего тела при плоскопараллельном движении – есть поворот
этого звена. А возможное перемещение всего тела при плоскопараллельном движении – есть поворот
на малый угол 





 вокруг оси, проходящей через мгновенный центр скоростей. Этот угол можно определить.
вокруг оси, проходящей через мгновенный центр скоростей. Этот угол можно определить.
Так как |
|
|
|
|
|
, то |
|
а |
|
|
|
|
|
перемещение |
||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
ползуна В: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и точки С: |
|
|
|
|
|
|
|
|
|
. То |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
есть перемещения всех точек механизма можно определить через одно возможное перемещение, перемещение звена ОА, через угол 




 .
.
Аналогично, поворотом на малый угол 





 вокруг мгновенного центра
вокруг мгновенного центра
скоростей 


 , определяются возможные перемещения точек колеса, которое может катиться без скольжения понеподвижной прямой (рис.64, г).
, определяются возможные перемещения точек колеса, которое может катиться без скольжения понеподвижной прямой (рис.64, г).
36
Работу сил, приложенных к материальной системе, на возможном перемещении будем называть возможной работой.
Если рассмотреть различные типы материальных систем, можно обнаружить, что элементарная работа реакций многих связей на возможном перемещении окажется равной нулю. Такие связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями. К таким связям относятся, например, все связи без трения.
Связи, |
которые |
не |
изменяются |
со |
временем, |
называются стационарными. |
|
|
|
||
Есть |
связи, |
которые |
называют |
или удерживающими, |
|
или односторонними, в зависимости от того препятствуют они перемещению точки во взаимно противоположных направлениях или только в одном.
37
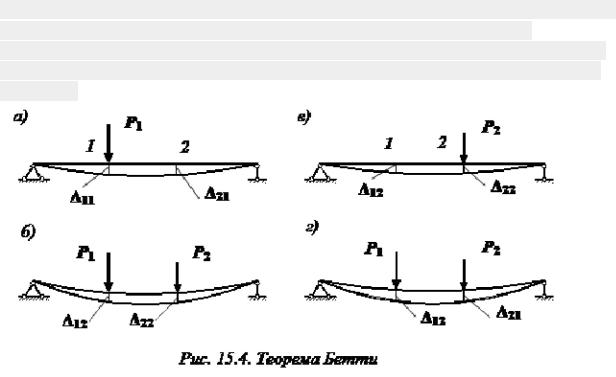
23. Теорема о взаимности работ (теорема Бетти)
Формулировка теоремы о взаимности работ (теоремы Бетти), доказанная в 1872
г Э. Бетти: возможная работа сил первого состояния на соответствующих перемещениях, вызванных силами второго состояния, равна возможной работе сил второго состояния на соответствующих перемещениях, вызванных силами первого состояния.
38
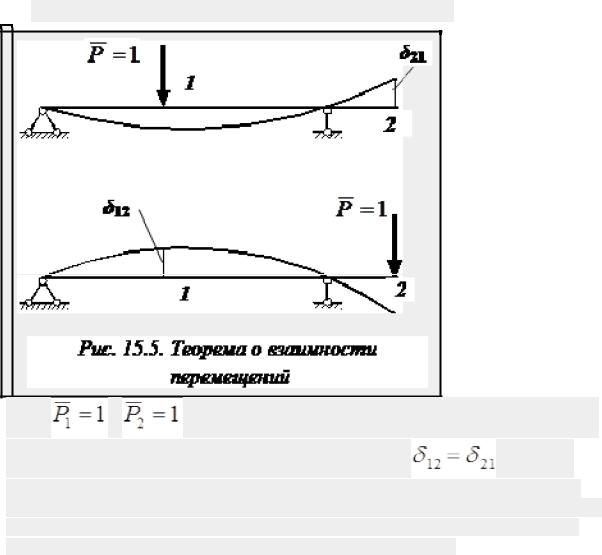
24. Теорема о взаимности перемещений (Максвелла) |
|
||
Пусть |
и |
. Теорема о взаимности перемещений с учетом принятого |
|
обозначения перемещения от единичной силы имеет вид: |
.Теорема о |
||
взаимности перемещений была доказана Максвеллом. Формулировка теоремы о |
|||
взаимности перемещений: перемещение точки приложения первой единичной силы, |
|||
вызванное действием второй силы, равно перемещению точки приложения второй |
|||
единичной силы, вызванному действием первой единичной силы |
|
||
39

25. теорема Релея о взаимноти реакций.
40
