Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лабораторные электричество

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

2.11 Mб

Скачать

☆

1 / 111 2 3 4 5 6 7 8 9 10 11 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ В. Н. КАРАЗИНА

ОСНОВЫ РАДИОЭЛЕКТРОНИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ

ХАРЬКОВ – 2008

УДК 621.375 ББК 32.846.я73 Ч34

Рекомендовано ученым советом радиофизического факультета Харьковского национального университета имени В. Н. Каразина (протокол № 5 от 23.05.08)

Рецензенты:

ст. науч. сотрудник ИРЭ НАН Украины им. О. Я. Усикова, доктор физ.-мат. наук, проф. А. А. Булгаков; зав. отд. космической радиофизики РИ НАН Украины, доктор физ.-мат. наук, проф. А. А. Минаков.

Ч34 Основы радиоэлектроники. Методические указания к выполнению лабораторних работ./ Ляховский А. Ф., Чеботарев В. И., Думин А. Н., Ляховский А. А. – Х.: ХНУ имени В. Н. Каразина, 2008. – 108 с.

В пособии приведены описания лабораторных работ по основным разделам курсов «Основы радиоэлектроники», «Основы современной электроники», таким как частотные характеристики цепей, электронное усиление сигналов, генерация электрических колебаний, цифровая электроника. Описания лабораторных работ содержат краткое изложение теоретического материала по данному вопросу, описание лабораторной установки, задания для самостоятельной подготовки к выполнению, задания и методические указания к выполнению лабораторной работы.

Пособие предназначено для использования при самостоятельной подготовке и во время выполнения лабораторных работ в учебной лаборатории студентами физических специальностей, которые изучают курсы «Основы радиоэлектроники» и «Основы современной электроники».

The descriptions of laboratory works on basic parts of courses “Fundamentals of Radioelectronics”, “Fundamentals of Modern Electronics” like frequency characteristics of circuits, electronic amplification of signals, generation of electric signals, digital electronics are given in the school-book. The descriptions of laboratory works contain the summary of theoretical study on the given work, the laboratory setup description, the tasks for studying on one’s own, the tasks and instructions for fulfillment.

The school-book is intended for students of physical professions who study the courses

“Fundamentals of Radioelectronics”, “Fundamentals of Modern Electronics” for training on one’s own and during fulfillment of the works in school laboratory.

У посібнику наведено опис лабораторних робіт із основних розділів курсів «Основи радіоелектроніки» й «Основи сучасної електроніки», таких як частотні характеристики кіл, електронне підсилення сигналів, генерація електричних коливань, цифрова електроніка. Описи лабораторних робіт містять короткий виклад теоретичного матеріалу з даного питання, опис лабораторної установки, завдання для самостійної підготовки до виконання, завдання та методичні вказівки до виконання лабораторної роботи.

Посібник призначено для використання під час самостійної підготовки та виконання лабораторних робіт у навчальній лабораторії студентами фізичних спеціальностей, що вивчають курси «Основи радіоелектроніки» й «Основи сучасної електроніки».

Лабораторная работа №1

ПРОСТЫЕ КОЛЕБАТЕЛЬНЫЕ ЦЕПИ

ЦЕЛЬ РАБОТЫ – экспериментальное исследование частотных характеристик и определение основных параметров колебательных цепей, применяемых для частотной селекции колебаний.

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Радиотехнический процесс, заключающийся в выделении из совокупности колебаний (сигналов) некоторого колебания (сигнала) заданной частоты или заданного интервала частоты, называют частотной фильтрацией (селекцией). Обычно этот процесс осуществляют с помощью колебательных цепей, используя явление резонанса. Основными характеристиками колебательных цепей являются их комплексные передаточные или входные функции K( ), связывающие комплексные амплитуды гармоник колебаний реакции и воздействия:

e j ВЫХ K( )S

K( )

e j argK

e j ВХ ,

ВЫХ

ВХ

где – частота гармоники.

Зависимость модуля комплексной функции от частоты называют

амплитудно-частотной характеристикой цепи (АЧХ), а зависимость аргумента от частоты – фазо-частотной характеристикой (ФЧХ).

АЧХ связывает амплитуды гармоник колебаний реакции и воздействия зависимостью

SВЫХ K( )SВХ ,

ФЧХ определяет связь фаз гармоник

ВЫХ ВХ argK( ).

1.Одиночный колебательный контур

Наиболее простой колебательной цепью является одиночный последовательный колебательный контур (рис. 1.1). Уравнение этого контура в комплексной форме имеет вид:

(R j L	1	)I E.	(1.1)
	j C
R	L
E	С

Рис. 1.1. Одиночный последовательный колебательный контур

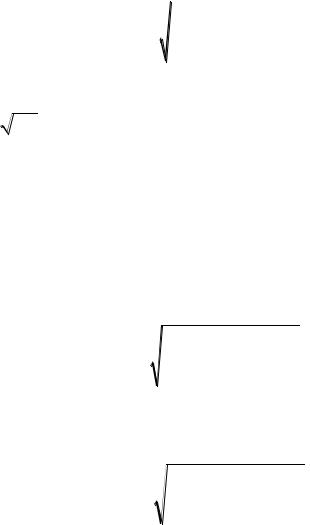
Если в качестве реакции рассматривается колебание тока I , то контур характеризуется комплексной входной проводимостью

YВХ	( )		1				1			GN ,	(1.2а)

				1					0
		R j	L		R 1	jQ


				C				0
				C				0

где	N( )		1


		1 Q2		0	2
					2

			0
			0

			0
	j arctgQ
	j arctgQ	0
e		0		.	(1.2б)
					(1.2б)

Здесь 0	1	– параметр контура, называемый “резонансной частотой”,


	LC
	LC

Q 0L – параметр, называемый “добротностью”. Физический смысл этих

параметров рассматривается ниже.

Если в качестве реакции рассматривается напряжение на емкости UC или напряжение на индуктивности UL , то

							Q 0														0
			U													j / 2 arctgQ			0
		( )	U																0
K				C											e								,
	C		E
													2

												0

					1 Q2

									0
									0
																							(1.3)
								Q												0
K ( ) UL								Q			0									0
K ( ) UL											0					e		0				.
																	j [ /2 arctgQ						]
		L
				E
												0		2



						1 Q2
						1 Q2				0
										0

Графики АЧХ, соответствующие функциям (1.2б) и (1.3), представлены на рис. 1.2. Часто эти графики называют резонансными кривыми, т. к. они характеризуют явление резонанса в контуре. Из графика рис. 1.2 следует, что в одной и той же цепи различные физические величины – амплитуды колебаний I , UC и UL достигают максимальных значений при различных

значениях частоты. Это обстоятельство обуславливает необходимость

уточнения понятия "резонансная частота".			Условились под резонансной
частотой	Р двухполюсной	цепи понимать	такое значение частоты, при
котором	входная функция	цепи (сопротивление или проводимость)
4

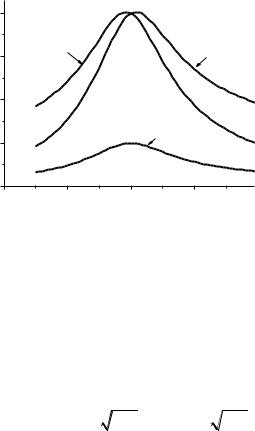
принимает вещественное значение. Т.е. при частоте, равной резонансной,
входное сопротивление или входная проводимость цепи являются
активными. Условие, определяющее значение Р , можно представить любым
из следующих выражений:
	ImZВХ ( Р ) 0,			argZВХ ( Р ) 0,	(1.4)
	ImYВХ ( Р ) 0,			argYВХ ( Р ) 0.	(1.4)
	ImYВХ ( Р ) 0,			argYВХ ( Р ) 0.
4	АЧХ
3		IKC( )I		IKL( )I
3
2
1			IN( I
1
0				1,2 0
0,6		0,8	1,0	1,2 0
Рис. 1.2. Амплитудно-частотная характеристика

В рассматриваемом колебательном контуре явление резонанса проявляется в резком нарастании амплитуд тока и напряжений на элементах цепи по мере приближения частоты вынужденных гармонических колебаний к резонансной частоте, которая на основании условий (1.4) равна

				1	,		f			1	.	(1.5)
					,		f				.	(1.5)
р	0			LC				р	2	LC
				LC					2	LC
При резонансе входная проводимость максимальная и является
активной величиной:
	Y	( )				1		.				(1.6)
	Y	( )						.				(1.6)
	ВХ		р			R
						R

Амплитуды напряжений на элементах емкости и индуктивности в этом случае в Q раз превышают амплитуду задающего напряжения источника

UC ( Р ) UL ( Р ) QE ,

(1.7)

поэтому резонанс в рассматриваемом контуре называют резонансом напряжений. Величина Q нередко достигает значений 102–104. С

энергетической точки зрения добротность характеризует отношение энергии, запасенной при резонансе в электрическом или магнитном полях контура

CU2

LI2

ЗАП

к энергии потерь в контуре за один период

RI2

T ,

ПОТ

где T0 1 f0

– период колебаний:

2 f LI2

I2L

ЗАП

(1.8)

I RT

ПОТ

Величина, обратная добротности, называется затуханием и обычно

обозначается d .

Кроме

значений 0

и Q колебательный контур характеризуется

параметром

который

называется

характеристическим

сопротивлением. При этом выражение, определяющее добротность контура, может быть записано в виде

Q		.	(1.9)

	R

Если резонанс в контуре достигается изменением величины одного из элементов L или C контура, то график зависимости амплитуды реакции от величины элемента называют настроечной кривой. Уравнение настроечной кривой получают, используя комплексную функцию цепи, полагая значениефиксированным, а величину L или C – переменной. Например, для зависимости тока в контуре от емкости, как следует из (1.1), имеем:

I(C)			E		.	(1.10)



		2		1 2
	R		L
	R		L
				C

На рис. 1.3 представлены настроечные кривые I(C) и I(L) .

На рис. 1.4 изображена схема одиночного параллельного колебательного контура, которая является дуальной цепью по отношению к одиночному последовательному колебательному контуру. Поэтому на основании принципа дуальности все выводы, характеристики, параметры и

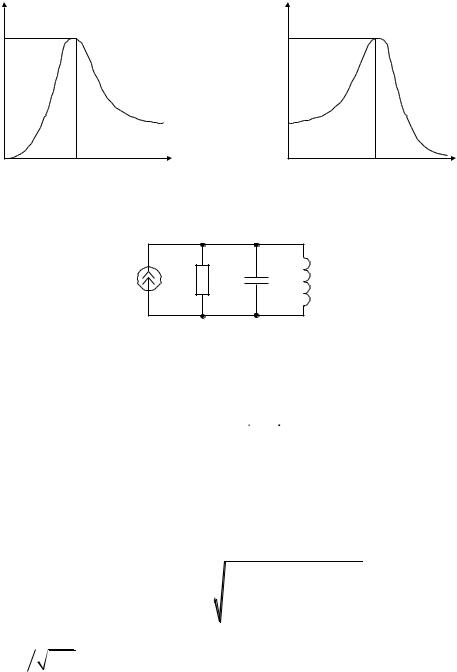
т.п., определенные для контура рис. 1.1, являются справедливыми для дуальных величин цепи рис. 1.4.

I
E
R
CP	C
Рис. 1.3. Настроечные кривые

I
E
R
LP	L

R С

Рис. 1.4. Одиночный параллельный колебательный контур

Так, уравнение цепи определяется выражением

			[G j( C		1	)]U I,									(1.11)
			[G j( C			)]U I,									(1.11)
					L
комплексное входное сопротивление равно
														0
		1					1					j arctgQ
Z ( )		1					1					j arctgQ	0
											e		0		, (1.1 2)
											e				, (1.1 2)
ВХ	G[1	jQ( / 0	0 / )]							2
	G[1	jQ( / 0	0 / )]	G 1 Q2					0	2
									0
								0
								0

где Р 0 1 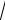LC , Q 0C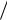G – параметры цепи.

Поскольку в этой цепи при условии = o амплитуды токов в ветвях одинаковы и в Q раз превышают амплитуду задающего тока, явление резонанса называют резонансом токов.

Естественно, что нормированные по максимуму функции (1.2а) и (1.12) совпадают. Уравнение, описывающее входную функцию колебательного контура, называют уравнением резонансной кривой:

N( )		1				.	(1.13)
		1



	1 Q2			0	2
					2

			0
			0

Резонансная кривая обладает свойством геометрической симметрии относительно резонансной частоты р (рис. 1.5), выражающимся в том, что для любой величины >0

N(	Р	)	N( )	.	(1.14)



			Р

Явление резонанса в рассмотренных цепях проявляется в том, что они существенно реагируют на колебания в некотором диапазоне частот, который называют "полосой пропускания". Обычно полосу пропускания контура или вообще какой-либо другой цепи определяют как интервал частот, в пределах которого АЧХ цепи составляет не менее 0,707 своего максимального значения. Для рассмотренных цепей граничные частоты ГРН

и ГР	определяются уравнением	n( ГР	) n( ГР	) 0,707 и полоса
	В	Н	В

пропускания равна

ГР	ГР	0	Q.	(1.15)
В	Н
IN( )I
1
P	P	P
2

Рис. 1.5. Резонансная кривая

Из этого уравнения следует формула, позволяющая определить значение добротности контура по экспериментальному графику резонансной кривой:

Q		0		f0
					.	(1.16)
			f	f	.	(1.16)
	ГР	ГР	ГР	ГР
	В	Н	В	Н

2.Связанные контуры

Вцелях частотной селекции широко используются также системы связанных контуров, обладающие лучшими характеристиками по сравнению

содиночными контурами.

Два контура называют связанными, если изменение электрического состояния одного контура вызывает соответствующее изменение состояния другого контура. На рис. 1.6 приведены схемы двухконтурных колебательных систем с индуктивной и емкостной связью. Степень связи контуров определяется коэффициентом связи kСВ . Для двух индуктивно

связанных контуров коэффициент связи равен kСВ M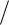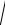L1L2 .

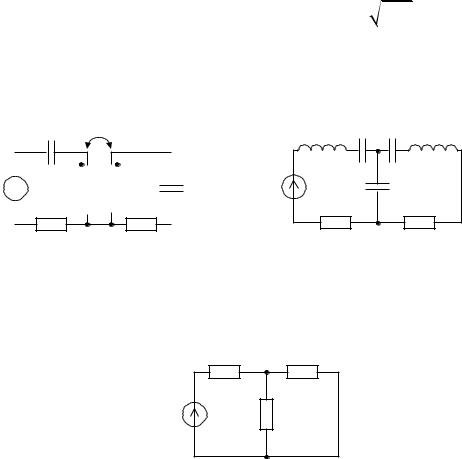
В общем случае, используя понятие комплексного сопротивления, систему двух связанных контуров можно представить эквивалентной схемой рис. 1.7.

C1 M

ER1 L1L2 R2 C2

а)

Рис.1.6. Связанные колебательные контуры: а) индуктивная связь, б) емкостная Т-образная связь

L1 C1 C2 L2

E CСВ

R1 R2

б)

Z1 Z2

ZСВ

Рис. 1.7. Эквивалентная схема системы связанных контуров

Система контурных уравнений для этой цепи в комплексной форме имеет вид:

		Z11I1	Z12I2 E,	(1.17)
		Z21I1 Z22I2 0.		(1.17)
		Z21I1 Z22I2 0.
Здесь Z11 Z1 ZСВ ,	Z22 Z2	ZСВ	– собственные сопротивления первого и
второго контуров;	Z12 = ZСВ	–	взаимное сопротивление контуров –

сопротивление связи, которое обычно является реактивным:

ZСВ jXСВ .

(1.18)

При условии (1.18) коэффициент связи определяется отношением

kСВ	XСВ	,	(1.19)

	X11X22

где X11 и X22 – реактивные сопротивления контуров, одноименные с

элементом связи.

Если в качестве реакции рассматривается колебание тока в первом контуре I1 , то цепь характеризуется комплексной входной проводимостью,

которая определяется выражением

YВХ ( )	Z22 ( )				.	(1.20)
	Z ( )Z	22	( ) Z2	( )
11			СВ

Если в качестве реакции рассматривается колебание тока во втором контуре I2 , то характеристикой цепи является комплексная передаточная

функция

K( )			ZСВ ( )					.		(1.21)
K( )		Z ( )Z		22	( ) Z2		( )	.		(1.21)
	11			22	СВ
Часто в качестве входной функции системы связанных контуров
рассматривают входное сопротивление
ZВХ ( )	1		Z11( )			Z2 ( )			.	(1.22)
ZВХ ( )			Z11( )				СВ		.	(1.22)
							СВ
	YВХ ( )						Z22 ( )

В этом выражении первое слагаемое – собственное сопротивление первого контура, а второе слагаемое – сопротивление, называемое "вносимым". При условии (1.18)

	X	2 R		X 2 X	22
ZВХ ( ) R11		СВ 22	j X11	СВ
	2	2		2	2
	R22	X22		R22 X22			(1.23)
R11 RВН ( ) j X11( ) XВН ( ) RВХ jXВХ .
Активная часть вносимого		сопротивления		RВН ( ) ,		учитывающая

потери энергии во втором контуре, увеличивает активную составляющую входного сопротивления. Реактивная часть вносимого сопротивления XВН ( ) , определяющая запасаемую во втором контуре энергию, изменяет

1 / 111 2 3 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.2015169.43 Кб21Лабораторная работа № 4. Текстовые функции.docx
#
22.08.2019651.26 Кб2Лабораторная работа № 6. Матричные операции. По...doc
#
23.02.2015222.72 Кб11Лабораторная работа №16.doc
#
23.02.2015131.07 Кб5Лабораторная работа1.doc
#
23.02.20151.83 Mб47Лабораторний практикум НВЧ(Шматько А.А.).pdf
#
23.02.20152.11 Mб50Лабораторные электричество.pdf
#
13.11.2019763.39 Кб15Лабораторный практикум по CSS.doc
#
12.11.20191.03 Mб39Лабораторный практикум по HTML.doc
#
13.11.2019138.24 Кб19Лабораторный практикум по PHP.doc
#
18.12.20182.2 Mб10Лаврик учебник.doc
#
31.10.2018136.7 Кб1Лайне Ненависть во взаимоотношениях между женщи....doc