Метода термодинамика(практика)
.pdf
50
5.ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ И ПАРАМЕТРЫ
5.1Начала термодинамики
П е р в о е н а ч а л о т е р м о д и н а м и к и (закон сохранения и превращения энергии для тепловых процессов) устанавливает, что изменение внутренней энергии dE макроскопической системы слагается из работы, произведенной ею над внешними телами (или внешними телами над ней) dW , и количества тепла, полученного (или отданного) системой dQ :
dE = dQ + dW . |
(5.1) |
Внутренняя энергия – однозначная функция состояния тела, тождественна его средней энергией ε, вычисленной по законам статистической физики
E ≡ ε = kT 2 ∂(ln Z(V , T )) ∂T , |
(5.2) |
где Z (V , T ) – функция состояний (см. разд. 3.4). К однозначным функциям состояния системы относится и энтропия S :
S = E
T + k ln Z + S0 ,
S = k ln Ω,
где S0 – абсолютная постоянная, Ω – число состояний системы.
К в а з и с т а т и ч е с к и м ( о б р а т и м ы м ) называется процесс, при котором система последовательно проходит ряд равновесных состояний. Число
состояний равновесной системы определяется её средней энергией – Ω(ε) , а
количество тепла – изменением энтропии dQ =T dS . Из (5.1) |
для обратимых |
процессов следует о с н о в н ое т е рм од и н а м и че с ко е |
ра в е нс т во |
dE = dW +T dS = −p dV +T dS , |
(5.5) |
т.е. в частном случае внутренняя энергия есть потенциал по отношению к
объему V и энтропии S , |
а сопряженные им давление p и температура T |
|
играют роль обобщенных сил. |
|
|
Энтропия замкнутой связана с вероятностью ее состояния ф о р м у л о й |
||
Б о л ь ц м а н а : |
|
|
|
S = k lnW + const . |
(5.6) |
В т о р о е н а ч а л о |
т е р м о д и н а м и к и : |
наиболее вероятным в |
51
замкнутых системах является процесс, при котором энтропия возрастает (необратимый процесс) или остается постоянной (обратимый процесс):
dS ≥ 0 . |
(5.7а) |
Для незамкнутых систем справедливо неравенство |
|
dS ≥ dQ T . |
(5.7б) |
Максимальная полезная работа достигается только при обратимых процессах независимо от природы (типа) тепловой машины. Поскольку внутренняя энергия и энтропия однозначные функции состояния, то
v∫dE = 0 , |
v∫dS = v∫dQ T = 0 , |
(5.8) |
где температура T – играет роль интегрирующего делителя. Если определить энтропию в некотором начальном состоянии через параметры (X0 , Y0 ) , то в состоянии, характеризуемом параметрами (X , Y ) , ее значение с точностью до аддитивной постоянной S0 равно
( X , Y ) |
|
|
S( X , Y ) = ∫ |
dQ T + S0 . |
(5.9) |
( X0 , |
Y0 ) |
|
Для квантовых систем, когда kT намного меньше разности энергий между нормальным и первым возбуждаемым уровнями kT << ∆ε, справедливо т р е т ь е н а ч а л о т е р м о д и н а м и к и . Оно гласит: энтропия
равновесной системы при весьма |
низких температурах стремится к абсолютной |
||
постоянной S0 (или к нулю, если |
S0 |
принять за начало отсчета): |
|
lim S = S0 |
, |
lim S = 0 . |
(5.10) |
T → 0 |
|
T → 0 |
|
5.2 Термодинамические потенциалы (характеристические функции).
В а д и а б а т и ч е с к и х |
п р о ц е с с а х , |
когда |
получаемым |
(отдаваемым) теплом dQ можно |
пренебречь ( dQ << dW ), |
работа тела |
|
выполняется за счет изменения его внутренней энергии dE = dW . В частности, если единственным обобщенным параметром является объем, то dE = −pdV .
К |
термодинамическим |
потенциалам |
относятся |
|
э н е р г и я |
F ≡ E −TS , т е п л о в а я ф у н к ц и я |
|||
H ≡ E + pV , |
п о т е н ц и а л |
Г и б б с а |
(основной |
|
с в о б о д н а я ( э н т а л ь п и я ) термодинамический
52
потенциал) Φ ≡ E −TS + pV . Изменение свободной энергии и потенциала Гиббса при изотермических процессах имеет смысл работы, а энтальпии – количество полученной теплоты в изобарном процессе ( p = const ).
|
При действии на систему еще и других обобщенных сил ( Λj |
или λj ), |
|||||
определяемых через сопряженные им параметры ( λj |
или Λj ), дифференциалы |
||||||
термодинамических потенциалов принимают вид: |
|
|
|
|
|||
|
|
|
dE(V , S, λj ) = −p dV +T dS + ∑Λj dλj |
, |
|
(5.11а) |
|
|
|
|
j |
|
|
|
|
|
|
|
dF(V , T, λj ) = −pdV − S dT + ∑Λj dλj |
, |
|
(5.11б) |
|
|
|
|
j |
|
|
|
|
|
|
|
dΦ( p, T , Λj ) =V dp − S dT − ∑λj |
dΛj , |
|
|
(5.11в) |
|
|
|
j |
|
|
|
|
|
|
|
dH ( p, S, Λj ) =V dp +T dS − ∑λj |
dΛj . |
|
|
(5.11г) |
|
|
|
j |
|
|
|
|
Если тело помещено в электрическое или магнитное поле, |
то из суммы ∑ |
||||||
остается только одно слагаемое, где в первом случае Λ = EG, |
λ = PG , во втором – |
||||||
ΛG |
= HG |
, Gλ = MG |
, а EG, HG – напряженности электрического и магнитного полей, |
||||
P |
и |
M – |
векторы электрической и магнитной поляризации. |
Так, для |
|||
потенциала Гиббса |
|
|
|
|
|||
|
|
|
dΦ(p, T, E)=V dp − S dT − PGdEG , |
|
|
(5.12a) |
|
|
|
|
dΦ(p, T, H )=V dp − S dT − MG dHG . |
|
|
(5.12б) |
|
Базовыми соотношениями теории систем с переменным числом частиц есть дифференциалы (5.11) с добавлением слагаемого µdN , в частности:
dE (V , S, N) = −p dV +T dS +µdN = −p dV +T dS +(Φ
N )dN .
Из (5.11) и (5.12) следует связь термодинамических параметров с частными производными характеристических функций
p = −(∂E ∂V )S ; T = (∂E ∂S )V ; p = −(∂F ∂V )T ; S = −(∂F ∂T )V ; |
(5.13а) |
|||
V = (∂Φ ∂p)T ; S = −(∂Φ ∂T )p ; V = (∂H ∂p)S ; T = (∂H ∂S )p ; |
(5.13б) |
|||
PG = −(∂Φ ∂EG) |
; |
M = −(∂Φ ∂HG ) |
. |
(5.14) |
|
p, T |
|
p, T |
|
Учитывая (5.3), определение |
свободной энергии и потенциала |
Гиббса, |
||
53
имеем
F = −kT ln Z(V , T ) ; |
Φ = −kT ln Z( p, T ) . |
(5.15) |
5.3Дифференциальные соотношения термодинамики. Уравнения ГиббсаГельмгольца
Из свойств дифференциалов, формул (5.11)–(5.14) следуют д и ф ф е р е н ц и а л ь н ы е с о о т н о ш е н и я т е р м о д и н а м и к и :
(∂p ∂S )V = −(∂T ∂V )S ; |
(∂p ∂T )V = (∂S ∂V )T ; |
|
(5.16а) |
||||||
(∂V ∂T )p = −(∂S ∂p)T ; |
(∂V ∂S )p |
|
= (∂T ∂p)S ; |
|
(5.16б) |
||||
(∂PG ∂p) |
G |
= −(∂V ∂EG) |
; |
(∂M ∂p) |
G |
= −(∂V ∂HG) |
; |
(5.16в) |
|
T , E |
T , p |
|
T , H |
|
|
T , p |
|
||
Связь между термодинамическими потенциалами дают |
у р а в н е н и я |
||||||||
Г и б б с а – Г е л ь м г о л ь ц а |
в |
дифференциальном и |
интегральном |
||||||
представлениях: |
|
|
|
|
|
|
|
|
|
E = F −T (∂F ∂T )V ; |
|
H = Φ −T (∂Φ ∂T )p ; |
(5.17) |
||||||
F = −T ∫E dT T 2 + const T ; |
Φ = −T ∫H dT T 2 + const T ; |
(5.18) |
|||||||
5.4 Тепловые и упругие коэффициенты. Критерии устойчивости
Т е п л о ё м к о с т ь есть функция процесса и определяет количество теплоты, необходимое для изменения температуры системы на один градус:
|
C ≡ δQ dT = (dE + p dV ) |
dT . |
(5.19) |
|
Если представить |
E |
как функцию |
температуры и |
объема |
dE (T, V ) = (∂E ∂T )V dT +(∂E ∂V )T dV , |
то общее выражение теплоемкостей в |
|
процессах с произвольным фиксированным параметром λ ( =V , p, S, E, HG,...) |
||
имеет вид |
|
|
|
|
(5.20) |
Cλ = CV + (∂E ∂V )T + p (∂V ∂T )λ , |
||
где CV = (∂E
∂T )V – теплоёмкость тела при изохорном ( λ ≡V = const ) процессе.
В произвольных к в а з и с т а т и ч е с к и х |
п р о ц е с с а х с λ = const |
|
Cλ = CV +T (∂p ∂T )V (∂V ∂T )λ , |
Cλ =T (∂S ∂T )λ , |
(5.21) |
54
C |
p |
= C +T (∂p ∂T ) (∂V ∂T ) |
p |
= C |
−T (∂V ∂T ) |
2 (∂p ∂V ) |
, (5.22) |
|||
|
V |
V |
V |
|
|
p |
|
T |
||
|
|
Cp |
= (∂H ∂T )p , |
|
|
Cp |
=T (∂S ∂T )p , |
|
(5.23) |
|
М а кс и ма л ь ны й к о эф ф иц и ен т |
п о л е зн о го |
д ей с т в ия |
||||||||
п е р и од и чес к и х |
т еп л о в ы х |
м аш и н : |
|
|
|
|||||
|
|
|
η= ∆W Q = (T1 −T2 ) |
T1 , |
|
|
(5.24) |
|||
где T1 , T2 – температуры нагревателя и холодильника, dW = Q −Q′– работа за цикл Карно, Q , Q′ – количество теплоты, полученной от нагревателя и отданной холодильнику, соответственно.
К о э ф ф и ц и е н т |
|
т е п л о в о г о |
р а с ш и р е н и я |
α и |
||||
т е р м и ч е с к и й к о э ф ф и ц и е н т д а в л е н и я β |
|
|
|
|||||
α = (∂V ∂T ) |
p |
V0 ; |
|
β = (∂p ∂T ) |
p0 . |
(5.25) |
||
|
|
|
|
V |
|
|
|
|
И з о т е р м и ч е с к а я |
æ |
T |
и а д и а б а т и ч е с к а я |
æ |
сжимаемости |
|||
|
|
|
|
|
|
S |
|
|
æT = −(∂V ∂p)T V0 ; |
æS = −(∂V ∂p)S |
V0 . |
(5.26) |
|||||
Эти параметры связаны между собой соотношениями |
|
|
|
|||||
α = p0 æT β; |
|
|
γ = æT æS = Cp |
CV . |
(5.27) |
|||
Энтропия идеального одноатомного газа (формула Сакура-Тетроде,
O.Sackur, H.Tetrode) |
|
|
|
||
|
S = Nk ln (V (kT )3 2 |
N )+ Nk (5 +3 ln (2πm h2 )) 2 . |
(5.28) |
||
У с л о в и я у с т о й ч и в о с т и р а в н о в е с и я о д н о р о д н о й |
|||||
с и с т е м ы : |
|
|
|
|
|
|
|
CV > 0 ; |
(∂p ∂V )T < 0 . |
(5.29) |
|
5.5 Примеры решения задач |
|
|
|
||
П р и м е р 1 . |
Определить разность Cp −CV |
для газа Ван-дер-Ваальса и |
|||
для идеального газа. |
|
|
|
||
Р е ш е н и е . |
За исходную |
рассмотрим формулу (5.22). Из |
уравнения |
||
состояния |
(p + a V 2 ) (V −b)= NkT находим |
(∂p ∂T )V = Nk (V −b) и |
|||
(∂V ∂T )p |
= Nk {p + a V 2 − 2a(V −b) V 3}. Тогда |
|
|
||
55
Cp −CV = Nk
(1− 2a(V −b)2 
V 3 NkT ).
В пренебрежении слагаемыми второго порядка малости ( ~ ab
V 2 ) имеем Cp −CV = Nk (1+ 2a / NkTV ). Для идеального газа ( a = 0, b = 0 ) Cp −CV = Nk .
П р и м е р 2 . Записать связь между термодинамическими параметрами
теплоизолированного идеального газа (уравнение Пуассона). |
|
||
Р е ш е н и е . Из (5.1) при dQ = 0 |
следует CV dT + pdV = 0 , а с учетом |
||
уравнения состояния ( p = NkT V ) |
и |
Nk = Cp −CV |
(пример. 1): |
dT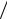
T +(γ −1)dV
V = 0, где γ = Cp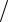 
CV . После интегрирования получаем первую форму уравнения Пуассона
TV γ−1 = const .
Замена T или V через p из уравнения состояния приводит ко второй и третьей формам уравнения Пуассона pV γ = const , T γ p1−γ = const .
П р и м е р 3 . Вычислить энтропию газа Ван-дер-Ваальса и найти уравнение его адиабаты.
Р е ш е н и е . Считая, что E = E (V , T ) , имеем dE = CV dT +(∂E
∂V )T dV .
Из |
(5.5) |
находим |
(∂E ∂V )T = −p +T (∂S ∂V )T |
= −p +T (∂p |
∂T )V |
и |
S = ∫(dE + p dV ) T . Для |
газа Ван-дер-Ваальса |
( (∂p ∂T )V = |
Nk (V −b) , |
|||
Пример. 1) получаем
S = ∫CV dT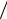
T + Nk ln(V −b) + S0 .
Т.к. CV слабо зависит от температуры, то |
S = CV lnT + Nk ln(V −b) + S0 . |
Для |
|||||
адиабатического процесса ( S = const ) |
T (V −b)N k CV = const . |
|
|
||||
П р и м е р |
4 . |
Показать, что |
при |
T → 0 |
изотермическая |
æT |
и |
адиабатическая |
æS |
сжимаемости |
вырожденных |
систем равны, |
т. |
е. |
|
(∂V
∂p)T =(∂V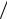
∂p)S .
Ре ш е н и е . Из перекрестных соотношений и теоремы Нернста имеем
(∂V
∂T )p = −(∂S
∂p)T = 0, (∂p
∂T )V = (∂S
∂V )T = 0 . После подстановки в (5.22)
получаем Cp = CV , а следовательно, æT æS = Cp CV =1.
|
|
|
|
56 |
|
|
|
|
|
П р и м е р |
5 . |
Показать, что закон Кюри для парамагнетиков χ = C T не |
|||||||
выполняется при низких температурах. |
|
= (∂MG |
|
|
|
||||
Р е ш е н и е . |
Из (5.12б) |
следует (∂S ∂H ) |
∂T )G |
. Согласно |
|||||
|
( MG = CHG |
|
|
T , p |
|
H , p |
|
||
закону Кюри |
T ), |
(∂M ∂T )G |
= −CHG |
T 2 . |
Но |
при |
низких |
||
|
|
|
|
H , p |
lim (∂S ∂HG ) |
|
|
|
|
температурах справедлива |
теорема Нернста |
= 0, и |
поэтому |
||||||
|
|
|
|
|
T → 0 |
|
T , p |
|
|
закон Кюри не выполняется. |
|
|
|
|
|
|
|||
П р и м е р |
6 . |
Установить связь между абсолютной T и эмпирической |
|||||||
температурой t , измеряемой в условной произвольной шкале каким-либо термометрическим телом (термометром).
Р е ш е н и е . |
Считаем внутреннюю энергию E функцией T и V . Тогда, |
||||
согласно (5.5), |
|
|
|
∂T )V dT T – полный дифферен- |
|
dS = (∂E ∂V )T |
+ p dV T +(∂E |
||||
циал, |
для |
|
которого |
справедливо |
(∂{ (∂E ∂V )T + p T} ∂T ) = |
= (∂{(∂E ∂T )V |
|
|
|
V |
|
T} |
∂V ) . Непосредственное вычисление левой и правой частей |
||||
|
|
|
T |
|
|
равенства приводит к уравнению (∂E
∂V )T + p =T (∂ p
∂T )V , которое позволяет найти функцию T = f (t) (или t = ϕ(T ) ). В силу существования такой зависимости (∂ p
∂T )V = (∂p
∂t)V (dt
dT ) оно преобразуется к виду:
dT
T = (∂ p
∂t)V dt
(∂E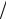
∂V )t + p .
Здесь правая часть – функция измеряемых параметров. После интегрирования
|
t |
|
|
|
|
|
|
|
T =T0 |
|
|
∂t)V dt |
|
=T0 |
exp I (t) , T1 =T0 exp I(t1) . |
||
exp ∫(∂ p |
(∂E ∂V )t |
+ p |
|
|||||
|
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Начальная температура T0 и соответствующая ей эмпирическая t0 задаются произвольно, что отвечает выбору единицы измерения температуры. Так, если взять температурную шкалу такой, чтобы разности между основными точками
двух |
|
произвольных |
эмпирических |
температур |
|
t |
−t |
0 |
=1000 С |
и |
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
τ (t ) − τ |
(t |
) =1000 X |
соответствовали |
разности абсолютных |
температур |
|||||||||||
1 |
1 |
0 |
0 |
|
|
|
|
|
|
(T1 −T0 ) = eI (t ) (eI (t1 ) −1) |
||||||
T1(t1) −T0 (t0 ) =1000 К и |
θ1(τ1) −θ0 (τ0 ) =1000 Y , то из T |
|
||||||||||||||
следует |
|
|
T =100e |
e |
|
−1 , |
θ=100e |
|
e |
|
|
−1 . |
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
I (t) |
I (t1 ) |
|
|
I (τ) |
I (τ1 ) |
|
|
|
|
||
Поскольку (∂... ∂t) dt = (∂... |
∂τ) (∂τ ∂t) dt , то I (τ) = I(t) и θ =T . Полученные |
|||||||||||||||
57
соотношения оказываются справедливыми, если вместо давления p и объема V выбрать любую другую обобщенную силу Λ и сопряженный ей параметр λ
t |
|
|
t |
|
|
I (t) = I(τ) = ∫(∂ p ∂t)V dt |
|
|
= ∫(∂Λ ∂t)λ dt |
|
|
(∂E ∂V )t |
+ p |
(∂E ∂λ)t |
+ Λ . |
||
t0 |
|
|
t0 |
|
|
Поэтому формула шкалы абсолютной температуры не зависит от выбора термометрического тела и позволяет найти T по произвольной эмпирической температуре, измеряемой по каким-либо его свойствам, например, кроме тепловых, оптическим или магнитным..
Если в качестве термометрического тела выбрать идеальный газ ( Λ = p ,
λ =V , p = p0 (1+βt) |
при V = const , |
β =1 273.15, t – температура по шкале |
||||
Цельсия, (∂E ∂V ) |
t |
= 0 ), то при t −t |
0 |
=1000 С. |
||
|
|
1 |
|
|
||
I (t) = ln[(1+βt) (1+βt0 )] |
, |
I (t1) = ln[(1+βt1) (1+βt0 )] . |
||||
|
|
|
T (t) =100[(1+βt) β(t1 −t0 )] = t + 273.15 . |
|||
Абсолютный ноль T = 00 К по шкале Цельсия равен t = −273.150 С.
5.6 Задачи и упражнения для самостоятельной работы
5.1.Вычислить работу идеального газа во время расширения при адиабатическом процессе. Указание: Воспользоваться уравнением состояния в форме Пуассона.
5.2.Определить свободную энергию и найти уравнение состояния системы, если ее энтропия равна S = RV0 (T
T0 )α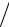 
V , где V0 , T0 , α – константы.
5.3.В макроскопической системе средняя энергия связана с температурой соотношением E = αT n , (n >1). Найти ее число состояний.
5.4.Энергия и импульс частиц связаны между собой соотношением ε = pc ,
где c – скорость света. Написать распределение Гиббса для частиц такого газа по энергиям, найти его термодинамические потенциалы.
5.5.Найти свободную и внутреннюю энергии, теплоемкость столба идеального газа высотой H и площадью S , находящегося в поле сил тяжести.
5.6.Идеальный газ состоит из N молекул с жесткими диполями d0 и находится в электрическом поле напряженности E при температуре T .
58
Определить его вектор поляризации и функцию состояний, если в отсутствие поля она равна Z0 .
5.7.Выразить непосредственно теплоемкость системы CV через функцию состояний.
5.8.N частиц идеального газа заключены в объем V и подчиняются микроканоническому распределению с энергией E . Вычислить для них фазовый объем Γ, энтропию S и температуру T .
5.9.Найти изменение энтропии при смешивании двух различных газов, имеющих одинаковые температуру и давление, но разные объемы V1 и V2 .
5.10.В двух сосудах находятся два однотипных идеальных газа с одинаковыми температурами T и числом атомов N , но с разными давлениями p1 и p2 . Сосуды соединяются. Найти изменение энтропии.
5.11.Определить связь между параметрами идеального газа в политропном процессе (изменение количества тепла dQ = C dT , где C – теплоемкость при
произвольных фиксированных параметрах).
5.12. Вычислить изменение энтропии идеального газа массы m и молекулярным весом атомов µ при его нагревании от температуры T1 до T2 . Рассмотреть изохорный и адиабатический процессы.
5.13.Получить свободную энергию смеси идеальных газов, состоящей из ν1 молей одного и ν2 молей другого компонента и занимавших до смешивания объемы V1 и V2 . Найти изменение свободной энергии при изотермической диффузии этих газов в объем V1 +V2 .
5.14.Вывести закон Дальтона для давления смеси двух идеальных газов.
5.15.Показать, что(∂CV 
∂V )T =T (∂2 p
∂T 2 )V .
5.16.Показать, что(∂Cp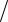 
∂ p)T = −T (∂2V
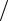∂T 2 )p .
5.17.Показать, что теплоемкость Cp системы не зависит от давления, если её объем пропорционален температуре.
5.18. Доказать, что на диаграммах ( p ↔V ) адиабата круче изотермы,
(∂ p
∂V )S > (∂ p
∂V )T .
5.19. Найти энтальпию системы, если её теплоемкость Cp = αT 3 ln p и
59
объем V =βT 4 
p , где α и β – постоянные величины.
5.20.Определить теплоемкость Cp , изотермическую сжимаемость æT и коэффициент теплового расширения через потенциал Гиббса.
5.21.Получить термодинамический потенциал Гиббса смеси идеальных газов, состоящих из ν1 молей одного и ν2 молей другого компонента и
занимавших до смешивания объемы V1 и V2 . Найти изменение потенциала Гиббса при изотермической диффузии этих газов в объем V1 +V2 .
5.22. |
Потенциал |
Гиббса |
системы |
представлен |
функцией |
Φ(T, p) = AT + BTp +Cp2 |
2 +T 2 2, |
где A, B , C |
– абсолютные постоянные. |
||
Найти энтальпию системы. |
|
|
|
||
5.23.Определить термоупругий эффект (∂T
∂ p)S системы при
адиабатическом процессе. Вычислить его для идеального газа, занимающего объем V и имеющего теплоемкость Cp .
5.24. Однотипные идеальные газы с одинаковыми температурой T0 и числом N атомов находятся в сосудах разного объема V1 и V2 . Определить максимальную полезную работу при их смешивании (соединении). Указание: воспользоваться формулой энтропии S = kN [ln (V
N) +1.5 lnT ]+ N S0 (m) .
5.25 Вычислить дополнительные энергию и теплоёмкость, приобретаемую газом из N молекул с жесткими диполями d0 в слабом (εd0 << kT ) электрическом поле с напряженностью ε.