
Метода термодинамика(практика)
.pdf
100
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
R |
|
потенциальная |
энергия |
u = mω2 r2 |
2 , |
где |
|
r2 = ∫r2dW (r) |
∫dW (r) . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
} |
|
0 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
m ω2 R2 2 kT |
m ω2 R2 2kT |
|
|||
|
|
|
|
|
|
|
|
||||||||||
После |
вычисления |
|
|
|
|
R |
|
|
|
e |
|
−1 . |
|||||
u = kT {1 + mω |
2kT −1 e |
|
|
|
|||||||||||||
4.26. |
q = e(m1−m2 ) ω2 R2 |
2 kT . |
4.27 |
Средняя |
|
энергия |
колебательного |
движения |
|||||||||
ε = p2 |
2m + æq2 |
2 . |
Поскольку dW ( p) dW (q) = Ce− p2 |
2 mkT dp e−æq2 2kT dq , |
то |
||||||||||||
∞ |
∞ |
∞ |
∞ |
|
|
|
p2 = ∫ p2 dW ( p) |
∫ dW ( p) , |
q2 = ∫ q2 dW (q) |
∫ dW (q) |
и |
|
= kT . |
ε |
||||||
− ∞ |
− ∞ |
− ∞ |
− ∞ |
|
|
|
4.28. Вероятность, что двухатомная молекула имеет компоненты угловой
скорости вблизи ω1 и |
ω2 |
дается выражением (см. 4.12): |
dW (ω1,ω2) = (I 2πkT )exp(−I ( |
ω12+ ω22 ) |
2kT )dω1dω2 , где I = m1m2a (m1 + m2 ) . |
Отсюда находим ω2j
εв = I (ω12 + ω22 ) 2 = kT .
2 = kT .
∞
= ∫ ω2jdW (ω j ) и среднюю энергию вращения
−∞
4.29. Число молекул газа, пополняющих один из
сосудов за единицу времени, равно ∆N = N1 − N2 . Число молекул N j , уходящих из j -го сосуда, определяется распределением Максвелла по проекциям
скорости, ортогональным сечению S : N j |
= Snj (m 2πkTj )1 2 ∞∫e− mv2 2kTj vdv . Здесь |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
плотность молекул |
учитывает |
состояние газа |
nj = pj kTj . Поэтому |
|||||||||||
M = m∆N = Sp(m 2πkT )1 2 ( |
2 −1). |
4.30. |
Число |
частиц, |
вылетающих со |
|||||||||
скоростью |
v |
|
через |
единицу |
площади |
за |
1 c : |
dn(v, θ≤ π 2)= |
||||||
= 2πnvdW (v) |
π 2 |
|
|
|
|
|
|
|
|
|
|
|||
∫ cosθsin θdθ. Если |
n0 – плотность молекул в пучке, то вероят- |
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
ность, что они имеют скорость v , есть dW1 (v) = dn(v) |
n0 . Отсюда |
|||||||||||||
|
|
∞ |
|
|
|
|
∞ |
|
|
∞ |
|
|
|
|
|
|
= ∫v dW1 (v) = ∫e−mv2 2kT v4dv |
∫e−mv2 2kT v3dv = (3 2)(πkT 2m)1 2 . |
|||||||||||
v |
||||||||||||||
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
||
Аналогично, |
|
|
Каждая молекула, имеющая ортогона- |
|||||||||||
|
v2 |
= 2(kT m)1 2 . 4.31. |
||||||||||||
льную к стенке |
|
v |
– проекцию скорости, при ударе передает ей энергию |
|||||||||||
ε(v ) = pmv2 |
2 . |
Число молекул, ударяющихся за 1 с о стенку, находится из |
||||||||||||

101
распределения Максвелла dν(v )= nv dW (v ). Получаемая при этом энергия
1 cм2 стенки от молекул с проекциями скоростей v [0, ∞] равна
∞
E = ∫ε(v ) dν(v ) = (pnm 4 π)(2kT
4 π)(2kT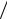 m)3
m)3 2 . 4.32. Если a – равновесное расстоя-
2 . 4.32. Если a – равновесное расстоя-
0
ние, а q – смещение атомов от положения равновесия, то l = a + q . Поскольку на атомы действуют силы упругости, то их потенциальная энергия равна
∞
U (q)= æq2  2 и q = ∫ qexp(−æq2 2kT )dq = 0 , l = a .
2 и q = ∫ qexp(−æq2 2kT )dq = 0 , l = a .
−∞
5.1. Динамика параметров газа при адиабатическом процессе описывается урав-
нением |
Пуассона |
|
(см. пример |
2): |
pV γ |
= p V γ |
= NkTV γ−1 . |
|
p = NkTV γ−1 V γ , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
2 |
2 |
1 |
1 |
|
|
|
|
|
|
|
1 |
1 |
|
||
W = |
V2 |
NkTV γ−1dV V |
γ = NkT |
1 |
−(V V )γ−1 |
(γ −1). |
|
|
F = − |
T |
SdT = RV T × |
|||||||||||||||||||||||
∫ |
5.2. |
|
∫ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
1 1 |
|
|
1 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
||||
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T0 |
|
|
|
|
|
|
|
|
× 1 − |
(T T )α+1 |
V (α +1), |
p = RV T |
1 −(T T )α+1 |
V 2 (α +1) . |
|
5.3. |
Поскольку |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω(E) = exp(S k) , |
CV = (∂E ∂T )V , |
S = T∫(CV dT T )= nαT n−1 |
(n −1), |
|
то |
Ω(E) = |
||||||||||||||||||||||||||||
|
|
( |
|
|
|
( |
|
) |
) |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
( |
|
|
) |
|
( |
|
|
) |
|
|
|
|
|
|
|
|
. 5.4. dw(ε) = 4πVe−ε kT ε2dε z(hc)3 ; z =8πV |
|
|
3 |
|
|
3 . Для |
||||||||||||||||||||||
= exp |
|
|
nE |
|
n −1 kT |
|
|
kT |
|
|
hc |
|
||||||||||||||||||||||
идеального |
газа |
|
Z = zN |
N !; |
F = −NkT ln (8πV (kT )3 e (hc)3 N ), |
|
p = nkT , |
|||||||||||||||||||||||||||
E = N |
|
= 3NkT ; |
CV = 3Nk . |
5.5. |
|
Z = zпостN |
zпотN |
N !, |
|
zпост = (2πmkT |
|
h2 )3 2 ; |
||||||||||||||||||||||
ε |
|
|
|
|||||||||||||||||||||||||||||||
zпот = kTS (1 − e−mgH kT ) mg . F = −NkT ln{e(2πmkT h2 )3 2 SkT (1 −e−mgH kT ) |
|
Nmg}, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
E = |
5NkT 2 − NmgH |
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
emgH kT −1 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
CV = 5Nk 2 − N (mgH )2 emgH kT |
kT 2 (emgH kT −1)2 ; |
|
при mgH kT <<1 |
CV ≈ 3Nk 2 , |
||||||||||||||||||||||||||||||
при mgH kT >>1 |
CV ≈ 5Nk 2 . 5.6 Дипольная молекула в электрическом поле |
|||||||||||||||||||||||||||||||||
|
GG |
приобретает дополнительную потенциальную энергию |
U = −(dE)= −d0 E cosθ. |
N
Функция состояний Z = Z0 ∫π ed0 E cos θ kT sin θdθ = Z0 (2kT d0 E)N sh N (d0 E kT ).
kT sin θdθ = Z0 (2kT d0 E)N sh N (d0 E kT ).
0

|
|
|
|
|
|
|
|
|
102 |
|
|
|
|
|
|
|
|
|
|
|
|
Вектор |
поляризации |
|
P = −(∂Ф ∂EG) = kT ∂(ln Z ) |
∂EG = Nd0 {cth(d0 E kT )− |
|||||||||||||||||
−kT d0E} EG |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
||
EG |
. В слабом электрическом поле ( d0E kT <<1): PG Nd02 EG |
3kT , |
|||||||||||||||||||
Z (E ) 2N 1 +(d0E kT )2 |
6 N . |
5.7. |
CV = 2kT (∂(ln Z ) |
∂T )+ kT 2 (∂2 (ln Z ) |
∂T 2 ). |
||||||||||||||||
5.8. |
Фазовый |
объем |
|
|
|
G |
G |
=V |
N |
G |
Область |
интегрирования |
в |
||||||||
Г(Е,V )= ∫dpdq |
|
∫dp . |
|||||||||||||||||||
пространстве импульсов определяется условием |
(p12 + p22 +... + p32N ) |
2m ≤ E |
и |
||||||||||||||||||
является с геометрической точки зрения шаром в 3N –мерном пространстве с |
|||||||||||||||||||||
радиусом |
R = |
2mE . |
Интеграл |
есть |
объем, |
пропорциональный |
|||||||||||||||
R3N = (2mE)3N 2 , |
т.е. |
Г(Е,V )= const V N E3N 2 . |
Энтропия |
|
S = k ln (Г h3N )= |
||||||||||||||||
= kN lnV + (3kN ln E) 2 + const . Температура |
T = ∂E ∂S = 2E 3kN . 5.9. Началь- |
||||||||||||||||||||
ная |
энтропия |
S 0 = S 0 + S0 |
= N k ln (V N )+ N f (T , m ) |
+ N |
k ln (V |
N |
2 |
)+ |
|||||||||||||
|
|
|
|
|
|
1 |
2 |
1 |
|
1 |
|
1 |
1 |
1 |
1 |
2 |
|
2 |
|
|
|
+N2 f (T1, |
m2 ), |
после |
|
смешивания |
S = N1k ln ((V1 +V2 ) |
N1 )+ N1 f (T1, m1 )+ |
|||||||||||||||
+N2k ln ((V1 +V2 ) |
N2 )+ N2 f (T1, m2 ). Ее изменение S − S0 = N1k ln ((V1 +V2 ) |
V1 )+ |
|||||||||||||||||||
+N2k ln ((V1 +V2 ) |
V2 )> 0 . |
|
5.10. |
|
Начальная |
энтропия |
|
системы |
|||||||||||||
S 0 = −Nk ln p p − 2Nf (T ), а |
после |
смешивания |
S = −2Nk ln p − 2Nf (T ), где |
||||||||||||||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 p1 p2 ). 5.11. Из |
|||||
p = 2NkT (V1 +V2 ). Изменение энтропии ∆S = Nk ln ((p1 + p2 )2 |
|||||||||||||||||||||
закона сохранения энергии dE = dQ − pdV и уравнения состояния p = NkT V с
V с
учетом dE = CV dT и равенства |
Cp −CV = Nk |
(см. |
пример |
2) |
имеем |
|||
CdT = CV dT + (Cp −CV )T dV V . После интегрирования |
получаем |
уравнение |
||||||
политропы для идеальных газов: |
TV n−1 = const , |
где |
n = (C |
p |
−C) (C |
|
−C) . |
|
|
|
|
|
|
V |
|
||
Другие формы уравнения политропы следуют из соответствующих замен через
уравнения |
|
состояния: T n pn−1 = const , pV n = const . Адиабатический ( dQ = 0 , |
C = CQ = 0 |
, |
n = γ) и изотермический ( dT = 0 , C = CT → ∞) процессы являются |
граничными случаями политропного процесса. Т. е. для реальных процессов
1 < n < γ . |
Частные случаи политропного процесса: |
изобарный ( C = Cp , n = 0 ) |
|
p = const |
и |
изохорный ( C = CV ). В последнем |
случае вместо уравнения |
pV n = const |
можно воспользоваться равносильным ему (Vp1 n = const , 1/ n = 0 ) |
||
V = const . 5.12 Энтропия идеального газа S = (m µ)Nk ln (VT 3
µ)Nk ln (VT 3 2 )+ f (m, N ) , а
2 )+ f (m, N ) , а
∆S = S2 − S1 = (m µ)Nk ln (V2T23 2 |
V1T13 2 ). |
При |
изохорном |
|
процессе |
||||
∆S |
= (m µ)C ln (T |
T ). В |
адиабатическом |
процессе (V |
V = (T T )1 γ−1 |
, |
|||
V |
V |
2 |
1 |
|
|
2 |
1 |
1 2 |
|

103
см. пример |
2) |
|
∆SQ = 0 . |
5.13. |
Свободная |
энергия |
до |
смешивания |
|||||||||
Fj0 = −νj NkT ln (Vj |
νj N )+ f (mj ,T ) |
, а после Fj = −νj NkT ln ((V1 +V2 ) |
νj N )+ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ f (mj ,T ) . Её изменение при изотермической диффузии ∆F = ∑(Fj − Fj0 )= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
= −NkT ν1 ln ((V1 +V2 ) |
V1 )+ ν2 ln ((V1 +V2 ) V2 ) < 0 . Если |
|
V1 =V2 , |
ν1 = ν2 =1, то |
|||||||||||||
∆F = −2NkT ln 2 . |
5.14. |
F = −kT ln (z1N1 z2N2 |
N1!N2 !)= F1 + F2 ; |
p = −(∂F ∂V )T = |
|||||||||||||
= p1 + p2 . |
5.15. |
При |
переменных |
V |
и |
T (∂CV |
∂V ) |
|
=T (∂2S ∂T∂V ) |
. Т.к. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
V |
||
(∂S ∂V )T = (∂p ∂T )V , |
то |
(∂CV ∂V )T =T (∂2 p ∂T 2 )V . |
5.16. |
Воспользоваться |
|||||||||||||
определением |
Cp ( p, |
T ) |
и |
(∂S ∂ p) |
= −(∂V ∂T ) |
p |
. |
|
5.17. |
См. № |
5.16. |
||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
5.18. (∂p ∂V )S
∂V )S  (∂p
(∂p ∂V )T = (∂S
∂V )T = (∂S ∂T )p
∂T )p  (∂S
(∂S ∂T )V = Cp
∂T )V = Cp  CV >1. 5.19. H = ∫CpdT = = (αT 4 ln p)
CV >1. 5.19. H = ∫CpdT = = (αT 4 ln p) 4 + A( p) ; V = (∂H
4 + A( p) ; V = (∂H ∂ p)S = αT 4 4 p +(∂A ∂ p)S ≡ βT 4
∂ p)S = αT 4 4 p +(∂A ∂ p)S ≡ βT 4  p , (∂A
p , (∂A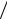 ∂p)S = 0 , A(p)= H0 . 5.20 Сp = −T (∂2Ф
∂p)S = 0 , A(p)= H0 . 5.20 Сp = −T (∂2Ф ∂T 2 )p , γТ = −T (∂2Ф
∂T 2 )p , γТ = −T (∂2Ф ∂p2 )
∂p2 )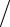 V ; α = (∂2Ф
V ; α = (∂2Ф ∂T∂p)p
∂T∂p)p  V0 .
V0 .
5.21. С учетом pV = νNkT выразить интеграл состояний как функцию давления
Z ( p, T ) |
и воспользоваться (5.15). Решение аналогично задаче 5.13. 5.22. Вос- |
|||||||||||||||||||||||
пользоваться |
|
уравнением |
Гиббса-Гемгольца, |
|
H = (Cp2 −T 2 ) 2 . |
5.23. |
Из |
|||||||||||||||||
дифференциальных соотношений |
(∂T ∂p)S = (∂V ∂S )p |
= (∂V ∂T )p |
(∂S ∂T )p = |
|||||||||||||||||||||
= αVT Cp . Для идеального газа (∂V ∂T )p = Nk p , |
(∂T ∂p)S |
=V Cp . 5.24. Изме- |
||||||||||||||||||||||
нение энтропии при смешивании |
∆S = −Nk |
{ |
ln |
|
4VV |
(V +V ) |
2 |
|
+3ln (T T ) . |
|||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
1 |
2 |
|
|
|
0 |
|
} |
|||
Максимальная полезная работа возможна в обратимом процессе ∆S = 0 , |
т.е. |
|||||||||||||||||||||||
при |
T =T0 {4V1V2 |
(V1 +V2 )2}1 3 . |
Отсюда |
|
|
∆W = −∆E =3Nk (T0 −T ) = |
||||||||||||||||||
= 3NkT |
|
|
4VV (V +V )2 |
1 3 |
|
|
5.25. |
Из |
|
|
№ |
5.6, |
имеем |
∆E (ε)= |
||||||||||
1 − |
|
. |
|
|
||||||||||||||||||||
0 |
|
|
1 |
2 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= kT 2 ∂ln Z ( |
ε,T ) |
∂T = −N (ε d |
0 |
)2 |
3kT C |
(ε) |
= ∂(∆E ) ∂T = (Nk 3)(εd |
0 |
kT )2 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку Cпост |
= 3Nk 2 , то |
C |
|
(ε)<< Cпост . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
V |
|
|
V |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6.1. Nk 2π2T 2εF . |
|
|
6.2. Из |
(5.22) и |
|
|
перекрестных |
соотношений |
|||
(∂V ∂T ) |
p |
= −(∂S ∂p) |
T |
; |
(∂p ∂T ) |
= (∂S ∂V ) |
T |
: |
Cp −CV ~ T 3 . |
6.3. |
z = |
|
|
|
V |
|
|
|
|
|
|||

104
= ∞ |
n +1 exp |
−hν |
( |
n +1 |
kT |
= −∂ |
∞ exp −hν |
( |
n +1 |
kT |
|
∂ |
( |
hν |
kT |
) |
, |
||
∑( |
) |
|
|
) |
|
|
∑ |
|
) |
|
|
|
|
|
|
||||
n=0 |
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
E = kT 2 ∂(ln zN ) |
∂T = NkT 2 ∂(ln ehν kT (ehν kT −1)−2 ) |
∂T = Nhν 1 + 2 |
(ehν kT −1) . |
||||||||||||||||
6.4. Учитывая (6.25), после вычисления |
S = ∫CV dT T |
воспользоваться (5.22): |
|||||||||||||||||
Cp −CV ~ T 7 . 6.5. ρ(ν, n(ν),T )=8πn3 (ν)hν3 1+ (ν n)(∂n
n)(∂n ∂ν)
∂ν)  c3 (ehν
c3 (ehν kT −1) .
kT −1) .
6.6. Поскольку при T = 00 K E = 3Nε |
F |
5 , то свободная энергия |
0 |
|
F = −T ∫(E0  T 2 )dT = E0 = (3Nh2
T 2 )dT = E0 = (3Nh2  10m)(3N
10m)(3N 8πV )2
8πV )2 3 . Из p = −(∂F
3 . Из p = −(∂F ∂V )T = 2E0
∂V )T = 2E0  3V
3V
следует pV 5 3 = const , |
что |
совпадает |
с уравнением |
адиабаты |
|
классического |
|||||||||||||||
идеального |
газа. 6.7. |
F = NkT ln (1 −e−hν kT ). 6.8. |
42000 K . 6.9. |
|
v = 2 kθD d h = |
||||||||||||||||
=12 км с. |
6.10. Число ударов электронов с |
импульсом |
p , |
|
ориентирован- |
||||||||||||||||
ным под |
углом |
θ |
|
к |
нормали |
стенки, |
равно |
|
их |
плотности |
|||||||||||
dn( p) = f 4πp2dpsin θdθ h3 , умноженной |
на |
объем |
|
( p cos θ) |
|
m. Т.к. |
f =1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
π 2 pF |
(p cosθ m)dn( p) = 2πmε2F |
|
|||||||||
при T = 00 K и |
f = 0 |
при T > 00 K , то ν = ∫ |
∫ |
h3 = |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
= (hπ 2m)(3n 8π)4 3 . 6.11. При |
T >>T |
функция состояний |
z |
в |
=T T . Считая |
||||||||||||||||
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
в |
|
|
интенсивность |
|
I ( j, T ) = An(εj ) |
N = A(Tв |
T ) |
(2 j +1)e |
− j( j+1)Tв T |
|
|
|
непрерывной |
|||||||||||
|
|
|
|
|
|
||||||||||||||||
функцией |
j , из условия |
∂I ∂j = 0 |
находим j(max) |
= ( |
2T Tв −1) |
2 . Максимум |
|||||||||||||||
излучения |
|
|
I ( jmax , T ) = A |
2Tв T exp{−(2 −Tв T ) |
|
4}≈ A 2Tв |
T (1 +Tв |
2T ) |
|||||||||||||
приходится |
на |
частоту |
(см. |
пример |
|
4) |
|
ν = (εj(max) +1 − εj(max) ) |
h = |
||||||||||||
= 2kTв ( j(max) +1) |
h = kTв (1 + |
2T Tв ) |
h . |
6.12. |
Излучение Солнца считается |
||||||||||||||||
равновесным, |
а |
при |
данных |
задачи |
hν |
1 |
kT 10−4 |
его |
|
|
спектральная |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
плотность описывается приближением (6.36). С учетом уменьшения мощности излучения по мере удаления от Солнца в ξ раз и ее связи со спектральной
плотностью (см. пример 5) |
имеем ξε(ν, T )dν = ξcρ(ν, T )dν 4 . |
Полная |
|||
мощность |
шумового |
сигнала, |
принимаемая антенной площадью |
S , равна |
|
2πS ξkT ν2 |
c2 2 10−14 Вт. 6.13. Т.к. плотность фотонов вблизи частоты ν |
||||
C |
|
|
|
|
|
равна dn(ν)= fф g (ν)dν, то |
из |
(6.30) при n(ν) =1 и (6.34) |
следует |
||
|
|
∞ |
|
∞ ∞ |
∞ |
N =8πV (kT hc)3 J , |
где J = ∫x2 e−x |
(1 −e−x ) dx = ∑∫x2e−nxdx = Г(3)∑1 n3 ≈ |
|||
|
|
0 |
|
n=1 0 |
n=1 |

105
≈ 2.6 . Уравнение адиабаты |
pV 4 3 = const находим из (6.39). 6.14. C = 4αVT 3 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Т.к. p = αT |
3 |
|
не зависит от объема V , а Cp = CV |
−T (∂p ∂T )V |
(∂p ∂V )T , то |
||||||||||||
|
|
||||||||||||||||
Cp → ∞. 6.15. |
|
Относительная заселенность n-го уровня энергии |
dN (n) N = |
||||||||||||||
= dw |
( |
n, (T |
T ) |
) |
= exp(−nT |
T ) |
∞ |
exp(−nT T ) |
= exp(−nT |
T ) |
1 −e−Tk T |
) |
, |
||||
|
k |
|
|
|
k |
|
∑ |
k |
k |
( |
|
|
|||||
n=0
d W (0, 0.5)= 0.864 , dW (1, 1) = 0.117 . 6.16. Энтропия колебательного ( p = k ) и
вращательного ( p = в) движений N молекул – |
Sp |
|
|
+T |
∂(ln zp ) |
|
|
|||||||||
= Nk ln zp |
∂T . |
|||||||||||||||
Характеристическая |
температура |
вращения – |
T = h2 (m + m ) |
8π2r2m m k |
||||||||||||
|
|
|
|
|
|
|
|
|
в |
|
c |
0 |
|
c |
|
0 |
2.70 K . |
Поскольку |
T T = 222 >>1, то функция |
состояний вращательного |
|||||||||||||
|
|
|
|
|
в |
|
= Nk (ln (T Tв )+1) 12.7 кал/ град.моль. |
|||||||||
движения |
zв ≈T Tв , |
а |
энтропия |
Sв |
||||||||||||
Характеристическая |
|
температура |
{ |
колебательного |
движения |
|||||||||||
|
|
|
|
|
|
|
−Tк T |
|
−Tк T |
|
|
−Tк T |
} |
|||
Tк = hv k = 3100 |
0 |
K , |
а |
энтропия |
Sк = |
Nk Tкe |
T (1 −e |
)−ln (1 −e |
) ≈ |
|||||||
|
|
|
|
|
|
|||||||||||
≈ Nke−Tк T (1 +T T )≈ 0.07 кал/ град.моль. |
|
|
|
|
|
|
|
|
|
|||||||
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.1. В состоянии равновесия тело не движется. Работа при движении его за счет
флуктуации |
∆W = Mv2 |
2 , |
где v – скорость макроскопического движения. |
||||||||||||||||||||||||||||||||
Вероятность |
флуктуации |
скорости |
w(v)~ exp(−∆W kT )~ exp(−Mv2 2kT ). |
||||||||||||||||||||||||||||||||
|
|
|
|
v0x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Отсюда |
= kT M |
и |
|
v2 |
= kT M . |
7.2. |
После |
возведения |
в квадрат и |
||||||||||||||||||||||||||
усреднения дифференциала тепловой функции |
∆H =V |
|
∆p +T∆S |
имеем (см. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пример 1) ( |
∆H ) |
|
|
−V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= kT CpT |
|
(∂p ∂V )S . 7.3. См. пример 1, (7.7а) и (7.13) |
|||||||||||||||||||||||||||||||||
|
∆T ∆p = (kT |
|
CV )(∂ p ∂T )V . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(kT |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
r∆T ,∆p = ∆T |
∆p |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
7.4. |
r∆V ,∆S = kT (∂V ∂T )p |
|
|
|
|
|
|
|
|
|
|
. Для |
идеального |
газа r∆V ,∆S = |
|||||||||||||||||||||
|
−kT (∂V ∂p)T kCp |
||||||||||||||||||||||||||||||||||
=1 |
|
5Nk 2 . 7.5. |
|
|
= kT . 7.6. ϕ2 = kT mgl . 7.7. Среднее число фермионов |
||||||||||||||||||||||||||||||
∆S∆T |
|||||||||||||||||||||||||||||||||||
«+» |
и |
|
бозонов |
«–» |
с |
энергией |
|
εj |
|
описывается |
распределением |
||||||||||||||||||||||||
|
|
= exp((εj −µ) |
kT )±1 − 1 . |
Так |
как |
(∆nj )2 |
= kT (∂n j |
|
∂µ) |
(пример 5), то |
|||||||||||||||||||||||||
|
nj± |
|
|||||||||||||||||||||||||||||||||
|
|
|
j+ (1 − |
|
j+ ), |
|
|
|
|
( |
|
j− ). |
|
|
|||||||||||||||||||||
|
(∆nj+ )2 |
|
= |
|
|
(∆nj− )2 |
= |
|
j− |
1 + |
|
Дисперсия числа |
фермионов |
||||||||||||||||||||||
|
|
n |
n |
n |
n |
||||||||||||||||||||||||||||||

106
обращается в нуль при n j+ = 0 и n j+ =1, хотя в случае n j+ = 0 относительная флуктуация равна ∞. Для бозонов относительная флуктуация остается
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
конечной, равной единице и при очень больших n j− . |
7.8. Дисперсия полного |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
(ε j −µ) / kT |
|
(εj −µ) / kT |
|
||
числа бозонов (см. 7.7) (∆N ) |
= ∑n j− (n j− +1)= ∑e |
. |
||||||||||||||
|
|
e |
|
−1 |
||||||||||||
|
|
|
j |
j |
|
|
|
|
|
|||||||
После перехода от суммы к интегралу, учитывая значения плотности состояний g(ν)dν =8πν2dν V  c3 (раздел 6.), энергии фотонов ε = hν и равенство нулю химического потенциала µ = 0 , имеем
c3 (раздел 6.), энергии фотонов ε = hν и равенство нулю химического потенциала µ = 0 , имеем
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
ehν kT |
|
|
8πV ν2dν |
|
|
8πV (kT )3 |
∞ |
|
ex x2dx |
||||||
|
|
|
(∆N ) |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
c3 |
= |
(ch)3 |
|
∫ |
|
|
|
|
. |
||||||
|
|
|
|
|
( |
|
hν kT |
) |
2 |
|
( |
x |
) |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
e |
|
|
|
|
|
|
|
|
|
0 |
e |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
−1 |
|
|
||||
∞ |
x |
2 |
dx |
∞ |
e |
−x |
x |
2 |
|
|
∞ |
∞ |
|
π |
2 |
|
|
|
|
|
|
|
|
|||||
Т.к. ∫ |
e x |
= ∫ |
|
|
dx |
= ∑ |
∫nx2e−nxdx = |
|
, то |
окончательно получаем |
||||||||||||||||||
x |
2 |
|
|
|
|
|
−x 2 |
|
|
|||||||||||||||||||
0 |
(e |
−1) |
0 |
|
(1 −e |
|
) |
|
n=1 0 |
|
3 |
|
|
|
|
|
|
|
|
|||||||||
(∆N )2 = (2πkT hc)3 V 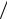 3 . 7.9. Используя алгоритм решения предыдущей задачи
3 . 7.9. Используя алгоритм решения предыдущей задачи
|
|
|
g(ε)dε = 4πV (2m h2 )3/ 2 |
|
|
εdε, |
|
|
= |
|
j (1 − |
|
j ), |
|
|
|
|
||||||||||||||||||||||||||
и значения |
|
εdε = A |
(∆nj )2 |
|
|
находим |
|||||||||||||||||||||||||||||||||||||
|
n |
n |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∞ |
|
ε(∂n ∂ε)dε, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(∆N ) |
2 |
= −AkT ∫ |
|
|
|
|
|
|
|
|
(ε−µ) kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
где n = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
e |
|
|
|
+1 |
|
|
. Вводится новая перемен- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ная x = (ε −µ) |
kT . Поскольку подынтегральная функция заметно отлична от |
||||||||||||||||||||||||||||||||||||||||||
нуля |
|
вблизи |
ε ≈ µ ( x = 0 ), |
а в |
силу |
неравенства |
µ kT >>1, то |
|
|
нижний |
|||||||||||||||||||||||||||||||||
предел |
интеграла |
считаем |
равным −∞ , а |
|
|
µ+ kTx |
|
µ + (kT |
2 |
|
µ) x − |
||||||||||||||||||||||||||||||||
− (kT )2 |
8 |
µ3 |
x2 |
+.... |
Так |
как |
|
|
|
функция |
|
|
∂n ∂x |
|
четная, |
|
|
|
(∞) = 0 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(∂n ∂x)dx . Интегриро- |
||||||||||||||||
|
|
|
|
|
|
|
(∆N ) |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
∫x |
2 |
||||||||||||||||||||
n(−∞) =1, |
то |
= AkT |
|
|
|
|
|
|
8 |
µ |
|||||||||||||||||||||||||||||||||
|
µ + 2 (kT ) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вание по частям дает∫x2 |
(∂n ∂x)dx = −2∫x (ex +1)−1 dx = −π2 6 . Дисперсия пол- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ного числа электронов (∆N )2 |
= 4πV (2m h2 )3/ 2 kT |
µ 1 −(πkT µ)2 24 . 7.10. Из |
|||||||||||||||||||||||||||||||||||||||||
№ 7.3 |
для |
идеального |
газа ( pV = NkT ) |
|
|
= N (kT )2 |
|
C V . |
С |
|
учетом |
||||||||||||||||||||||||||||||||
|
∆T ∆p |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
||
уравнения |
|
|
адиабаты |
( pV γ |
= const ) |
|
|
|
|
(∂p ∂V ) |
S |
= −γ p V |
|
и |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆p2 = γ p2 N = γkpT V , |
где |
γ = C |
p |
C . |
|
Отсюда |
|
r |
|
= Nk C |
p |
= 2 / 5 . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
∆p,∆T |
|
|
|
|
|
|
|
|
|||||||

107
7.11. С ростом заряда конденсатора на величину ∆q его энергия увеличивается
на ∆W = (∆q)2 |
2C . Вероятность |
заряда |
конденсатора |
– w(∆q) ~ e− (∆q)2 |
2kTC . |
|||||||||
Сравнение |
ее |
с |
распределением |
Гаусса |
определяет |
масштаб |
флуктуаций |
|||||||
|
|
= |
|
|
(∆I )2 = kT |
|
|
|
|
|||||
|
(∆q)2 |
kTC . |
7.12. |
L . 7.13. |
Скорость |
дрейфа |
электронов |
|||||||
v = I enS , |
а время пролета |
проводника |
длиной l равно t0 = l |
v = Slen I . |
||||||||||
Полоса |
частот |
|
дробового |
шума |
заключена |
между |
нулем и |
1 2t0 , |
т.е. |
|||||
∆f Д = I |
2Slen =10 10−3 |
(2 10−2 1,6 10−19 l n) ; а) ∆f Д = 30 кГц; б) ∆f Д = 300 Гц. |
||||||||||||
7.14. Для проводника с l =1 см, n =1016 см –3, |
ρ =1 Ω cм частоты дробового |
|||||||||||||
шума лежат в интервале от 0 до 300 Гц (задача 7.13) усилителем не
воспринимаются. |
|
Для проводника с l =10−1 см, n =1015 см – 3, ρ =10 Ω cм, |
||||
R =100 Ω . |
|
2eIR2∆f = 2 1,6 10−19 10−2 104 9600 = 0,44 мкВ. |
||||
|
(∆Uдр)2 |
= |
||||
|
4kTR ∆f = |
4 1,38 10−23 300 100 9600 = 0,12 мкВ. |
||||
7.15. |
(∆UT )2 |
= |
||||

|
108 |
|
|
ПРИЛОЖЕНИЯ |
|
П.1. Значения некоторых физических величин |
|
|
Число Авогадро |
NA |
6,02 1023 моль−1 |
Число Лошмидта*
Объем 1 моля идеального газа при нормальных условиях
Атомная единица массы
Постоянная Больцмана Ускорение свободного падения
Универсальная газовая постоянная
Скорость света Масса электрона Масса протона Постоянная Планка
Заряд электрона
NL |
2,69 1025 |
м−3 |
|
V |
2,24 10−2 |
м3 |
|
0 |
|
|
|
а. е. м. |
1,66 10−27 |
кг |
|
k |
1,38 10−23 Дж** град |
||
g |
9,81 м с2 |
|
|
NAk = R |
8,31 Дж моль град |
||
c |
3,00 108 м с |
||
me |
9,11 10−31 кг |
||
mp |
1,67 10−27 |
кг |
|
h |
6,63 10−34 |
Дж с |
|
h 2π = = |
1,05 10−34 |
Дж с |
|
e |
1,6 10−19 А с |
||
h2 8π2k |
40,27 10−47 |
кг м2 град |
|
h2 8π2c |
27,99 10−45 |
кг м |
|
hc k |
1,44 10−2 |
м град |
|
Ангстрем |
o |
10−10 м |
A |
*) Число молекул в 1 м3 вещества, находящегося в состоянии идеального газа
при нормальных |
условиях: температура – |
T = 2930 |
K , давление – |
|
|
|
|
0 |
|
p =10,13 104 |
кг м−1 |
с−2 =1 атм. |
|
|
0 |
|
|
|
|
**) 1 Дж =1 Н м =1 кг м2 с− 2

109
П.2. Типовые индивидуальные задания контрольных работ
Первые вопросы:
1. |
Вычислить интеграл ∫∞ (p3 −2 p +1) exp (− p2 |
2mθ)dp . |
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
2. |
Оценить с точностью до 0.01 интеграл |
0∫.1 xα exp (−4x2 )dx , |
для α =1, α = 2 . |
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
3. |
Как изменится элемент площади dx dy |
при переходе от переменных (x, y) к (u, v) , если |
||||||||
преобразование осуществляется по формулам |
u = axey , |
v = bxy . |
|
|
|
|||||
4. |
Любое из |
общего числа |
N однотипных событий |
реализуется с вероятностью |
w . |
|||||
Вероятность |
одновременной |
реализации k |
таких событий |
описывается |
биномиальным |
|||||
распределением W (k )= N !wk pN −k k!(N −k )! , p =1− w . Найти среднее |
значение |
|
и |
|||||||
k |
||||||||||
|
|
N |
|
|
|
|
|
|
|
|
N
дисперсию (∆k )2 . Указание: Воспользоваться тождеством (yw + p)N = ∑WN (k )yk .
|
k=0 |
5. Распределение случайной величины x задано функцией |
f (x)= Ae−(x−2)2 . Найти |
вероятность того, что значение случайной величины не превышает |
x +0.1. |
6.Показать, что распределение Пуассона ak e−a  k! удовлетворяет условию нормировки.
k! удовлетворяет условию нормировки.
7.Через какой промежуток времени следует менять все n транзисторов в приемнике, чтобы обеспечить его работу с вероятностью 0.90. Гарантийный срок службы транзисторов τ
часов, вероятность выхода из строя за время t любого из них p = t τ.
τ.
8.Показать, что для газа c весьма большим числом атомов справедливо соотношение exp (−ε)= exp (−ε), где ε – энергия атома.
9.Найти относительную флуктуацию абсолютной величины импульса и энергии молекулы идеального газа.
10.Определить среднюю ε и наиболее вероятную εmax энергию газа из N свободных атомов, помещенного в объем V , при температуре T . Объем фазового пространства описывается формулой Γ = constV N ε3N 2 .
2 .
11.Найти при температуре T функцию состояний линейного гармонического осциллятора, энергия которого равна ε = hν(n +1 2), n = 0, 1, 2,... , и все уровни колебательной энергии
2), n = 0, 1, 2,... , и все уровни колебательной энергии
невырожденные.
12.Определить при температуре T функцию состояний частицы, движущейся со скоростью c , если ее энергия и импульс связаны соотношением ε = pc .
13.Энергия линейного осциллятора ε = p2 2m + æq2 2 , где p и q – обобщенные импульс и
