Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метода термодинамика(практика)

.pdf

Скачиваний:

259

Добавлен:

23.02.2015

Размер:

1.14 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

9.УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ. ОТВЕТЫ.

1.1.Интегралы сводятся к Γ-функциям. 1.2. Воспользоваться формулами

для интеграла Пуассона. 1.3. Сделать замену y = x + a . 1.4. Разложить экспоненциальную функцию в ряд и провести почленное интегрирование. 1.6. Воспользоваться свойствами якобиана преобразования 1.8. x = r cos ϕ,

y = r sin ϕ,

D(x, y) D(r, ϕ) = r .

1.9.

r2 sin ϕ. 1.11. а)

да;

б)

нет,

кроме y =1;

в) нет. 1.12. а) abey

x(1 − y)

; б) 2

x2 − y2

x2 + y2 .

1.13.

а) Необходимым

условиям

экстремума

( fx′ = 0 ,

fy′ = 0 )

соответствуют

точки

M1 (0, 0)

M2 (1, 1) . Достаточное

условие

′′

′′ 2

только

для

fxx fyy −[ fxy ] > 0 выполняется

M2 (1, 1) . Поскольку fxx′′(1, 1) > 0 , то в M2 (1, 1) функция минимальна. 1.14. а) да; б) нет; в) нет; г) нет. 1.15. а) F(x, y) ≈ (x + y)[1 + (x − y)2] . 1.16. Представить функцию x2 рядом Фурье (1.18) на интервале [−π; π] . После вычисления

an = (1π) ∫ x2 cos nx dx подставить в полученное представление значения x = 0

−π

иx = π. 1.17. Представить функцию x4 рядом Фурье на интервале [−π; π] и

следовать указаниям к 1.16. 1.18. Функцию (ex −1)− 1 представить суммой бесконечно убывающей геометрической прогрессии со знаменателем e− x для

∞	∞	∞ ∞
x > 0 : ∫x3e− x ∑e− nxdx = ∑∫x3e− jxdx . Замена			jx = y и использование
0	n=0	j=1 0

соотношения предыдущей задачи дает требуемое доказательство.

2.1. 1.−0,29 ; 0,064 .

2.−0,784 . 3.−0,216 . 2.2. 1,2 ;

0,72 ;

0,707 .

2.3. После

∞

представления интеграла

∫ ...e−

dy в

виде суммы

∫ ...ey dy + ∫...e− ydy

− ∞

вычисления дают

(∆x)2

= 2 ,

δx =1, 41. 2.4.

−0,11;

2 3;

4 3; 8 9 .

∞

2.5. m ≥ lg(1 − P)

lg(1 − p) .

2.6.

A = 1

∫ dx (1 + x2 )

=1 π2 ;

x = y = 0 ;

− ∞

w(x [x1, x2 ]) = (1 π)arctg[(x1 − x2 )		(1 + x1x2 )] ;		w(x [−1, 1]) = 0,5 ;
w(x, y [−1, 1]) = 0.25 .			= (2πδ2 )− 1/ 2	∞∫ x4e− x2 2δ2 dx = 3δ2 ;
w(x, y [−1, 1]) = 0.25 .	2.7.	x4	= (2πδ2 )− 1/ 2	∞∫ x4e− x2 2δ2 dx = 3δ2 ;	δ2 ≡	x2	.
				− ∞

2.8. 1 −(1 −136)24 ≈ 0, 4914 . 2.9. а) Вероятность выпадения шестерки в любом из

бросаний

равна

W (1) = C1 (1 −1 6)

6 =

(1 −1 6)m−1 .

W (1) = 0,402 .

(m −1)! 6

б)

1 −(1 −1 6)6 0,665 . 2.10.

а)

1 16 ;

б)

7 16 .

2.11.

Наибольший отрезок

принимается за единицу, два других можно изобразить в виде

x -ой и

y -ой

координаты

точки

в плоскости

XY .

Условие

положительной реализации

x + y >1, т.е. половина квадрата,

разделенного диагональю x + y =1. Отв.

0,5.

2.12. Вероятность работы лампы за время t + ∆t

определяется произведением

вероятностей

независимых

событий

P(t + ∆t) = P(t) P(∆t) = P(t)(1 −α∆t) .

Учитывая

малость

∆t , имеем

P(t + ∆t) ≈ P(t) +(∂P ∂t) ∆t .

Из уравнения

P′ P = − α

следует

P(t) = Ce− α t . В

момент t = t0

лампа

работала,

т.е.

P(t0 ) =1 = Ce− α t0 , а P(t) = e− α (t−t0 ) . 2.13. Вероятность выхода из строя лампы за

гарантированный срок равна	w(τ) = qτ =1,	а за время t	− w(t) = t τ.
Вероятность работы системы	из n ламп −	P (t) = (1 −t τ)n .	Если считать
		n

невозможным эксплуатацию системы, когда Pn (t0 ) меньше заданной

вероятности

P ,

то

P =[1 −t0

τ]n . Отсюда

следует

t0 ≤ (1 − P1 n )

τ.

2.14.

Поскольку

1 − P <<1,

то, согласно 2.13,

P = 0,9 ≈1 − nt0

t0 = (1 − P) τ n =16,6 час.

2.15.

τ = nt (1 − P) = 60000 час.

2.16.

Надежность

работы

одного

комплекта

H1 =1 − P1 ,

где

P1 = n 100 ,

аппаратуры

комплектами

равна

=1 − Pm .

Увеличение

надежности

есть

= (1 − Pm )

(1 − P) .

2.17.

k =1,05 .

2.18.

Вероятность

нахождения

молекулы на высоте

z равна отношению объемов dV (z) V ,

где V = πR2 H 3 ,

dV (z) = πr2dz = π[(H − z)R H ]2 dz .

Отсюда

f (z) = 3(H − z)2

H 3 .

2.19.

0,328.

2.20.

(b + a)

2 ;

(a2 + ab +b2 )

3 ;

(a −b)2

12 .

2.21.

Для

гармонических

колебаний x = Asin(2πt T ) , где T

− период. Вероятность нахождения точки в

интервале dx равна отношению времени прохождения ею этого интервала dxx

к T2 , т.е. dw(dt) = dx[πAcos(2πtT )]; dw(x) = dx(π A2 − x2 ). 2.22. 12π.

2.23. (sin α) 2 .

2.24. x = a π 2 .

2.25. Чтобы ближайший сосед

молекулы

находился на расстоянии между r

и r + dr , необходимо: 1) наличие соседа (эта

вероятность равна α dV = 4πr2 αdr );

и 2)

расстояние между ними должно

быть не меньше

r . Вероятность

того, что ближайший сосед находится на

расстоянии, меньшем

r , равна

P = ∫ f (ξ) dξ, а большем r

–

(1 − P ). Эти

′

события независимы,

поэтому:

f (r) dr = 1 −

∫ f (ξ) dξ α

4πr

dr ,

(r) f (r) =

= −4παr2 + 2 r ;

f (r) = Cr2e− 4π α r3 3 .

Определив

C = 4πα

из

условия

нормировки, получим

f (r) = 4παr2 exp(−4παr3 3). Существует экстремальное

значение r = r0

( f ′(r0 ) = 0 ), отвечающее наиболее

вероятному

расстоянию

между ближайшими соседями. 2.26. f (h) = r2 (r2 + h2 )− 32 , (см. 2.23). 2.27. Углы

падения ϕ и преломления ψ связаны

равенством

sin ϕ = æsinψ. После

дифференцирования cos ϕ dϕ = æ cosψ dψ имеем dϕ= æ cosψ dψ

1 − æ2sin2ψ .

Поскольку f (ψ) dψ = C sin ϕ dϕ, то

f (ψ) = C æ2 sin ψ cos ψ

1 − æ2 sin2 ψ .

I. Для æ <1

– существует

полное внутреннее отражение. Преломление

имеет

место только

для

углов

0 ≤ ϕ≤ arcsin æ ,

0 ≤ ψ ≤ π 2 .

Отсюда следует

π 2

æ2 sin ψcosψ dψ

=1; C =1 (1 −

) и функция

условие нормировки

∫ C

1 − æ

1-æ

sin

f (ψ) dψ =

æ2 sin 2ψ dψ

распределения для углов преломления

2(1 − 1 − æ2

)

1 − æ2 sin2 ψ

π 2

II.

Для

æ >1:

0 < ϕ< π 2 ;

0 < ψ < arcsin æ−1 ,

C ∫ sin ϕ dϕ =1,

f (ψ) dψ = æ2 sin 2ψ dψ (2

1 − æ2 sin2 ψ ).

2.28.

Вероятность

прохождения

молекулой пути

x + dx без столкновения равна W (x + dx) =W (x) dW (dx) =

=W (x)(1 − adx) . Представив левую часть линейной функцией малого параметра

W (x) + (∂W∂x) dx +... =W (x) − aW (x) dx , получаем ∂W ∂ x = −aW (x) ,

W (x) = Ae− ax . Считая W (0) =1 = A , находим W (x) = e− ax . Средняя длина пробега

∞

равна λ ≡ x = ∫xdp , где dp =W (x)a dx − есть вероятность свободного

прохождения молекулой пути x с последующим столкновением: λ ≡ x =1 a . Поскольку функция W (x) = e− xλ не связана с точкой отсчета в пространстве, то возможно экспериментальное определение λ путем измерения отношения количества молекул пучка, «осевших» на двух разнесенных в вакууме полупрозрачных сетках. 2.29. Вероятность угадать произвольное число из N

есть w =1 N ,			а – n «счастливых» чисел определяется распределением Бер-
нулли	W	(n)	= Cn wn (1 − w)N −n .	W (3) ≈ 0,06 ;	W (6) ≈ 0.00042 . 2.30. Данные
	N		N	49	49

задачи позволяют считать, что N >>1, w <<1 и использовать распределение

Пуассона,

в котором

среднее

число

потерянных целей

= Nw =1.

а) Вероятность

потери

s целей

равна

WN (s) = (

)s e−

s!;

W0 (1) = e− 1 ;

W (2) = e−1

2 .

б)

Вероятность

потери

хотя бы

целей –

m−1

PN (m) = ∑(

)k e−

k! =1 − ∑(n )k e−

k!: PN (1) =1 −e− 1 ; PN (2) =1 − 2e− 1 .

k =m

k =0

3.1. Фазовая траектория − прямая, параллельная оси q . 3.2. Из закона сохранения энергии следует уравнение параболы z = z0 + p02 2m2 g − p2 2m2 g . 3.4. За время t вершины ∆A1 A2 A3 переместятся в точки фазового пространства

′		′		′	, z3 ) ,	где p1 = p0 − mgt ,	z1 = z0 + p0 t	m − gt	2	2 ,
A1( p1, z1) ,		A2 ( p2 , z2 ) ,		A3 ( p3
p2 = p1 ,	z2 = z1 + a ,			p3 = p1 +b,		z3 = z1 +bt m . Из	равенства	площадей
∆A1 A2 A3	и	′ ′ ′	следует		справедливость теоремы		Лиувилля.	3.5. После
		∆A1 A2 A3

соударения размерность фазового пространства сокращается вдвое, так как шары начинают двигаться как единое целое. Поэтому якобиан преобразования имеет две одинаковые строки и равен нулю. 3.6. Поскольку скорость постоянна, то начальный импульс p0 = const , а при отражении меняет знак вблизи стенок q = ±l . Это изменение происходит не мгновенно, а непрерывно под действием

упругой силы со стороны стенки −kq : кинетическая энергия частицы p2 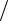2m переходит в потенциальную kq2 2 , и в фазовом пространстве соответствующие

p0
части траектории – дуги эллипса. 3.7. Γ = ∫	zdp = 2 p03	3m2 g . 3.8. Из закона
− p0
сохранения энергии ∫r (ee1 r2 ) dr = (p02 − p2 )	2m и	p0 = mv0 = 0 следует

p = 2mee [1 r −1 r ] . 3.9. x = x + ( p2							− p2 ) 2eEm .			3.10. а) Решая уравнение
	1	0				0	0
движения	mq = −γq			с начальными			условиями			[ q(t = 0) = v0 ,	q(t = 0) = q0 ],
найдем	q = q + mv		0	γ − mv	0	e− γt m γ,	v = v	0	e− γt m	и фазовую	траекторию
	0		0		0			0
q = q0 + m(v0 − v)		γ.		При движении системы по фазовой траектории из точки

(q0 , v0 ) в точку (q, v) ее элементарный фазовый объем становится равным

dvdq = D(v, q) D(v0 , q0 ) dv0 dq0 = e− γtm dv0 dq0 . Т.е. фазовый объем с течением времени экспоненциально уменьшается. Теорема Лиувилля выполняется при отсутствии трения ( γ = 0 ).

б) Уравнение движения

mq + mω02 q = −γq

(см. Пример 2). Решение его

учетом малости γ

( 4ω2m2 >> γ2 ) и

начальных

условий [ v(t = 0) = − q ω ]

q = q e− γt m cos ω

t ,

q = v = q e− γt m

sin ω

t описывает фазовую траекторию в

виде эллипса с убывающими со временем по закону e− γt m полуосями:

=1.

q2e− 2γt m

q2 ω2 e− 2γt m

Изменение

фазового объема

равно

e− γt m .

3.11.

Ω(ε)dε = 1 h3

)

(∂Γ ∂ε)dε,

(

Γ = 4πε3V

3c3 , Ω(ε)dε = (4πVε2 c3h3 )

dε. 3.12. Координатыx1 ,

x2 ,

x3 можно

принять

за

обобщенные,

тогда

им

соответствуют обобщенные

импульсы

p1 = 2mεcosωt ,

p2 = 2m(ε + ∆ε) cosωt ,

p3 =

2mεcos(ωt + δ) .

Площадь

треугольника выразим через координаты его вершин

S =

= m

ε∆ε sin δ.

Независимость площади треугольника от времени и доказывает справедливость теоремы Лиувилля для трех гармонических осцилляторов. 3.13. Координаты и импульсы до и после соударения соответственно равны qi , pi и qi′, pi′. Из

закона сохранения				′	′	,	2	2	2m2 =
закона сохранения			импульса и энергии p1 + p2 = p1		+ p2	,	p1	2m1 + p2	2m2 =
′2	′2	2m2	следует
= p1	2m1 + p2	2m2	следует
	p1′ = (m1 − m2 ) p1			(m1 + m2 ) + 2m1 p2 (m1 + m2 ) ,			q1′ = q1 ;
	′	= (m1	− m2 ) p2	(m1 + m2 ) + 2m2 p1 (m1 + m2 ) ,			′	= q2 .
	p2	= (m1	− m2 ) p2	(m1 + m2 ) + 2m2 p1 (m1 + m2 ) ,			q2	= q2 .

Якобиан преобразования равен	′	′	′	′	=	′	′	= −1, т.е. объем
Якобиан преобразования равен	D( p1	, p2	,q1	,q2 )	=	D( p1	, p2 )	= −1, т.е. объем
	D( p , p ,q ,q )					D( p , p )
	1	2	1	2		1	2

фазового пространства сохраняется. 3.14. Фазовое пространство для данной

системы

четырехмерное.

Условие

сохранения

фазового

объема:

′ ′ ′ ′

Т.к.

координаты

шаров

до

после

dv1dv2dx1dx2 = dv1dv2dx1dx2 .

столкновения одинаковы, то

dx dx

′

, а

dv dv

′

. С

течением

= dx dx

= dv dv

1 2

времени все точки фазового объема

dv dx

перемещаются параллельно оси x

(горизонтальный желоб!), однако эти смещения за одинаковый промежуток времени будут тем больше, чем больше скорость v . Поэтому прямоугольный элемент фазового объема со временем примет вид параллелограмма, а величина объема не изменится. 3.15. Задача сводится к вычислению интеграла

Γ = ∫ ∫ ∫			∫ dϕ dθ dpϕ dpθ			по	области,	ограниченной		поверхностью
	(ϕ) (θ) ( pϕ ) ( pθ )
H = const .			Пределы			интегрирования		ϕ [0, 2π] ,		θ [0, π],
p −sin θ			2mr2 H − p2 ; sin θ			2mr2 H − p2 .		После	замены	переменной
ϕ				0			0
p = sin u 2mr2 H				имеем	Γ = 4πmr2 H . 3.16. Из				распределения Гиббса
θ
dw(H ) = C e−H kT (∂Γ ∂H ) dH .						Из	задачи	3.15	∂Γ ∂H = 4πmr2 , и
	− H kT			∂H ≠ 0 ,	т.е. данное распределение не имеет максимума, и
∂ e		(∂Γ ∂H )		∂H ≠ 0 ,	т.е. данное распределение не имеет максимума, и

поэтому не существует наивероятнейшей энергии, а, следовательно, устойчивого состояния системы. 3.17. Поскольку для весьма большого числа

частиц			множитель			распределения	Гиббса		e− ε θ ∂Γ ∂ε ≈ δ(ε −ε ) , то
		= F (			), где F(ε)	− произвольная		функция	энергии. Отсюда следует
	F(ε)	= F (		ε	), где F(ε)	− произвольная		функция	энергии. Отсюда следует
требуемое доказательство. 3.18. См. указания к 3.17. 3.19. z =1										[2sh (hν 2kT )].
				∞
3.20. z = ∑e− j( j+1)Tв T (2 j +1) , где Tв = h2								8π2 I k . При высоких		температурах
				j=0
					∞
Tв <<T					z ≈ ∫e−x( x+1)Tв	T (2x +1) dx =Tв	T .	При	низких	температурах
			0

z ≈1 +3exp[−2Tв T ] . 3.21. z = (2πmkT h2 )32 V . 3.22. Элемент фазового объема d Γ = 4πVε2dεc3 , а z =8πV (kThc)3 .

4.1.

а)

W (vx ≤ v0 ) =W1 = (m 2πkT )1 2 ∫ e− mv2x

2kT dvx .

После замены

− ∞

переменных v

= (2kT m)1 2 x

( v

= 0,1 (2kT m)1 2 ,

x = 0,1)

имеем

−x

0,1

−x

0,1

∞

n x

2 n

∫

∑(−1)

dx ≈ 0,56 ;

W1 =

dx +

n=0

− ∞

б) W (v

, v

≤ v

) =W

;

в)

W (v

, v

≤ v

) =W

. 4.2. Элемент фазового

объема и характер распределения Максвелла не изменится. Сместятся его

(∆ε)2

−

2 , δε

максимумы. 4.3. Из (4.7), (4.15) находим

ε2

= 2 3 , δE =

2 3N .

4.4.

dN = 2(S N V )(2kT πm)1 2 sin θcos θdθ.

4.5. ε

вер

= kT 2 ,

mv2

2 = kT .

вер

4.6 dN = 2π( pV kT )(1 −cosα)(m 2πkT )3 2 e− mv2

2kT v2dv , M = mdN = (Mr

NA )dN .

∞

4.7.

Воспользоваться

формулами

= ∫v2dW (v) ,

v2x

= 2∫v2xdW (vx ) ,

−

2 . 4.8. В единицу времени через отверстие S

(∆v)2

пройдет Sv dn(v )

молекул с проекцией скорости v , нормальной к отверстию. Общее их число

∞

( 0 ≤ v ≤ ∞): dN dt = S0n(m 2πkT )1 2 ∫v e− mv 2kT dv = pS0 (2πmkT )− 1 2 . 4.9 Из

(4.16) находим среднюю относительную скорость молекул основного газа и

1 2

, где

′

примеси u = (2 π )(2kT µ)

µ = mm (m + m ) . Их число столкновений за

единицу

времени

равно

ν = nσef

(4.17), где

σef = π (

σ + σ′ ) 4π ≈

≈ (σ+ σ′ ) 2 . Так

как

средняя скорость движения молекул основного газа

= (2

π )(2kT m)1 2 ,

то

длина

свободного

пробега

равна λ = v v =

= (1 σef n)(m′(m + m′))12 . 4.10. Пусть v0 − относительная скорость бесконечно разделенных молекул, r0 − прицельное расстояние ( r0 vG0 ) (Рис. 9.1). Законы сохранения энергии и момента импульса ( mvG0 ×rG0 = m[(rG + rϕG) ×rG) ) в полярных координатах: m(r + r2 ϕ2 )− 2αrn = m v02 ; mr2ϕ = mr0 v0 . Исключая угловую ско-

рость, находим r2 + r02 v02 r2 − 2αmrn = v20 В точке наибольшего сближения молекул радиальная скорость r обращается в нуль. При этом минимальное расстояние между молекулами rmin находится из условия v02 (r02 rmin2 −1)= 2αmrminn .

Если rmin ≤ 2R , где R − радиус твердой сферы ( v = ∞), то молекулы сталкиваются, если rmin > 2R , они пролетают, не соприкасаясь друг с другом.

Условие соприкосновения rmin = 2R = D будет выполнено для прицельного

расстояния	r02 = D2 (1 + 2α mv02 Dn ).				Соответствующее эффективное сечение
2	2	2	n
σ = πr0 = πD	1+ 2α mv0 D				R
зависит от относительной					R
скорости.	Притяжение				ϕ
между молекулами увели-					ϕ
между молекулами увели-						r
чивает эффективное сече-				rmin		r
чивает эффективное сече-
ние. Возрастание		сечения				β
ние. Возрастание		сечения			r0
пропорционально					r0
	2	n
1 + 2α	mv0 D	,				v 0
т.е. зависит от отношения						v 0
потенциальной		энергии			Рис. 9.1
притяжения	и кинетичес-

кой энергии движения ( mv02 2 ). При большой относительной скорости искривление пути, вызванное притяжением, оказывается небольшим и мало сказывается на значении сечения.

Среднее значение эффективного сечения (формула Сюзереленда) зависит от

температуры: σ = πD2 1 +(2α mDn )(1v20 ) = πD2 (1+ const T ) . С ее увеличе-

нием σ стремится к величине геометрического сечения. От конкретного вида

взаимодействия ( α, n ) зависит значение	const . 4.11. P = (n 6) ∫v 2 pdW . Так
как v = (∂ε ∂p), то давление
∞	∞

p = (Nl 3V )∫α pl (4πV ) f ( p) p2dp = (Nl 3V )∫ε dW = lNε 3V = lE 3V .

0 0

4.12. Считая молекулу твердым телом с главными моментами инерции							I j и
проекциями угловых	скоростей ωj	на оси	инерции,	находим вероятность
3	∞
dW = ∏{ e− ε j kT dωj	∫ e− εj kT dωj},	где	εj = I j ω2j	2 .	4.13.	n1	n2 =
j=1	− ∞

					98
= πerf (1) − 2e−1				π(1−erf (1)) + 2e−1 , где erf (1) = 0,84 . 4.14 Если плотность

воды ρж , то эффективная масса mef одной частицы равна mef = m −ρж V .									Из
барометрической			формулы		находится плотность		распределения	зерен
ρ(z) = ρ	0	e−mef gzNA RT .		Т.к.	ρ(H ) ρ = 0,5 ,	то	H = (RT ln 2) m N		A	g ,
	0				0			ef	A
NA = RT ln 2 mef gH ,				dNA NA = α = dH H . 4.15. m = µ NA , z = kT mg = 7,5 км.
4.16. Число молекул в бесконечном столбе воздуха с основанием 1 см2								равно

∞∞

n∞ = ∫n(z) dz = ∫n0e−mgz kT dz = n0 (kT mg) = n0 7,5 105 , где			n0 = 2,69 1019 cм− 3	–
0		0
плотность молекул у поверхности Земли (число Лошмидта). n = 2,11 1025				=
			∞
= 2,11 1025 N	A	=35 моль. Масса бесконечного столба	воздуха M = µn =
	A		∞

= 29 35 г 1кг, авес P = Mg = 9,8 Н . 4.17. u = kT {1 − mgh(kT [exp(mghkT ) −1])}.

4.18. См. пример 7. Учитывая зависимость ρ(r) = m′n(r) , плотность белка вблизи оси ρ(0) = m′n(0) = n0 (R)exp(−m′ω2R2 2kT ) , ρ(R) = m′n0 (R) . Масса белка

− exp(

′

2kT )

−m ω

−(R −b)

M (R −b ≤ r ≤ R) = 2πlm′ ∫ n(r)r dr = M

′

2 2

R−b

1 −exp(−m

ω R 2kT )

→

4.19. Выделим на поверхности сферы площадку ∆S

= I R2dψ, где dψ − элемент

→

телесного угла с нормалью I , направленной во внешнюю область. На ней построим цилиндр, образующие которого численно равны абсолютной скорости атома, а ось составляет угол θ с нормалью к поверхности. Через эту поверхность за единицу времени вылетят все находящиеся внутри цилиндра

			mv2
атомы, для	которых	vcosθ ≥ 0 : dν(v) = ∆S vn 2π(m 2πkT )3 2 e− 2kT v2dv ×
π 2
× ∫ sin θd (sin θ) . Для преодоления силы притяжения атомы должны обладать
0
кинетической	энергией,	удовлетворяющей	условию mv02 2 ≥ γMm R . Число
атомов, покидающих поверхность планеты			4πR2 за единицу времени равно

∞

ν = 4πR2nπ(m2πkT )3 2 ∫e− mv2 2kT v3dv = 4πR2n(kT2πm)1 2 e−γmM kTR (1+ γmM kTR) .

∞

4.20. h = z = ∫zdW (z) , (∆h)2 = z2 − z2 . 4.21. Потенциальная энергия отдельной

молекулы массы m , находящейся на расстоянии r от центра массы,

U (r) = − γmM r .

Из

формулы

Больцмана

следует

n(r) = AeγmM rkT .

Т.к.

∞

∫n(r)4πr2dr = ∞,

то

система

неравновесная,

применение

распределения

Больцмана

неправомерно.

4.22.

Распределение

невзаимодействующих

W (rGj ) = Aexp(−U (rGj ) kT ),

молекул

W (rG1,rG2 ,....,rGN ) = ∏W (rGj ) ,

где

rj –

j=1

координата

j –ой молекулы. Вероятность, что n произвольных молекул из N

находятся

в объеме

]

v ,

остальные

объёме

V − v ,

равна

[

N −n , где P(v) =

∫

dW (rG) dv – вероятность, что молекула

W (n) = Cn Pn (v) 1

− P(v)

имеет координаты внутри

объема

v .

Рассмотрим

частные случаи: а) Для

N >> n ,

асимптотика

W (n) ≈ (NP)n (1 − P)N

при

N → ∞

и P → 0 ,

если

λ = lim NP ,

приводит

распределению

Пуассона: W (n) = lim W (n) =

N →∞

P→0

= lim λn (1 −λ N )N

n! = λne−λ n!. Среднее число частиц,

находящихся в объеме

N →∞

∞

v ,

= ∑nW (n) = λ. б)

Для

N >>1

n >>1

с учетом формулы Стирлинга

n=1

lnWN (n)= nln λ −λ − ln n! = nln λ −λ − nln+ n . Поскольку при n >>1 отклонение от среднего n −λ << λ , то ln n ≡ ln λ [1 + (n −λ) λ] ≈ ln λ + (n −λ) λ − −(n −λ)2 2λ2 +... и lnW (n) ≈ (n −λ)2 (2λ − n)2λ2 ≈ −(n − n )2 2n . Рассматри-

вая полученную гауссовскую функцию W (n) = Ce− (n−n)2 2n как непрерывную, при нахождении C воспользуемся интегральной формулой нормировки. Пределы интегрирования ввиду резкого спада функции при отклонении от

∞

среднего значения

выберем

от

−

∞ до

∞ C =1 ∫ exp(−

(n −

)dn =

−∞

2π

. 4.23. ε =1 + 4πn(α + p2

3kT ) . 4.24. Центр тяжести газа одного сорта

частиц zi = kT mi g − h (exp(mi g kT ) −1); центр тяжести системы:

z0 = ∑Nmi z j

∑Nmi

= lkT g − h∑mi

(exp(mi g kT )−1)

∑mi

i=1

4.25.

Вероятность

нахождения

молекулы

на расстоянии

от

центра

центрифуги (см.

задачу

4.18)

равна

dW (r) = Cemω2r2 2kT rdr .

Средняя

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.03.2016230.91 Кб5Методічка-психологія.doc
#
06.11.2018182.78 Кб1Методічка-психологія.doc
#
23.02.20158.79 Mб54Метода по лабам ТВП.doc
#
23.02.20152.13 Mб66Метода по ТВП(Яцук).doc
#
23.02.20152.65 Mб37Метода термодинамика(лекции).pdf
#
23.02.20151.14 Mб259Метода термодинамика(практика).pdf
#
27.11.2019595.97 Кб9Методики диагностики одаренных учащихся.doc
#
23.02.20154.7 Mб156Методики психодиагностики в спорте.doc
#
03.05.201529.58 Кб5Методики.docx
#
23.02.2015650.75 Кб23методич. минер. и микро.doc
#
05.05.2019867.11 Кб4методические указания СЭС 2010 лекции практика...docx