Алгоритм проведення прямих вимірювань та обробки їх результатів

Підкреслимо, що спочатку необхідно визначитися, з якою відносною похибкою потрібно виміряти фізичну величину та який очікуваний порядок цієї величини. Відповідно до цього добирають засіб вимірювання, знаючи його діапазон вимірювання, ціну поділки та інструментальну похибку. Створюють нормальні умови для його застосування та готують засіб до вимірювання. Перевіряють наявність похибки відліку нуля. За потреби налагоджують прилад.

Коли наперед відомо, що систематична похибка приладу перевищує випадкову похибку, то виконують одне вимірювання. Якщо ні, то проводять не менш як три вимірювання, результати яких записують у відповідну таблицю.

Тепер наведемо спрощену послідовність проведення розрахунків абсолютної похибки кількох прямих вимірювань однієї і тієї самої фізичної величини, яка найчастіше використовується в навчальних лабораторіях:

1. Як найближче до істинного значення вимірюваної величини потрібно взяти середнє арифметичне значення всіх вимірювань, яке визначається за формулою (3).

2. Треба за формулою (4) підрахувати випадкові відхилення від середнього арифметичного.

3. Знайти середнє значення абсолютної похибки за формулою (5).

4. Кінцевий результат прямих вимірювань записують у такому вигляді:

. (6)

Для зручності запису чисел слід користуватися десятковими кратними і частковими одиницями, утвореними від одиниць Інтернаціональної системи (CI), або десятковими множниками. Наприклад, замість можна записатиабоКінцевий же результат треба подавати в CI. Крім одиниць CI у деяких випадках допускається використання системи одиниць СГС. Дані щодо деяких одиниць цих систем і співвідношень між ними та іншими позасистемними одиницями містяться в Додатку №.4.

Похибки непрямих вимірювань.

У багатьох випадках шукану величину неможливо виміряти безпосередньо приладом, тому потрібно вимірювати інші величини, математична залежність від яких шуканої величини відома.

Загальні правила підрахунку похибок непрямих, або посередніх вимірювань можна дістати тільки за допомогою використання математичної теорії похибок і методів диференціального числення.

Алгоритм обробки результатів непрямих вимірювань

Похибки посередніх вимірювань визначаються за похибками безпосередньо вимірюваних величин. Безпосередньо вимірювані величини вважатимемо аргументами, а посередньо вимірювані – функціями. Розглянемо спочатку найпростіший випадок. Нехай, а абсолютна похибка прямого вимірювання величиниX дорівнює. Очевидно, що

. (7)

Розкладаючи праву частину виразу (7) у ряд Тейлора, матимемо:

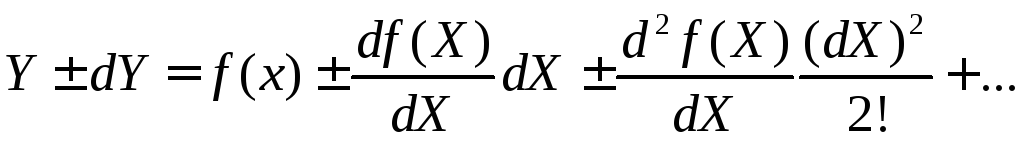(8)

Нехтуючи членами розкладу, які мають у степені, вищому за перший, дістаємо:

. (9)

Замінивши після диференціювання символдиференціалуна символ, що позначає абсолютну похибку, матимемо:

(10)

Отже абсолютна похибка функції одного аргументу дорівнює добутку похідної цієї функції на абсолютну похибку її аргументу.

Для відносної похибки з (10) дістаємо:

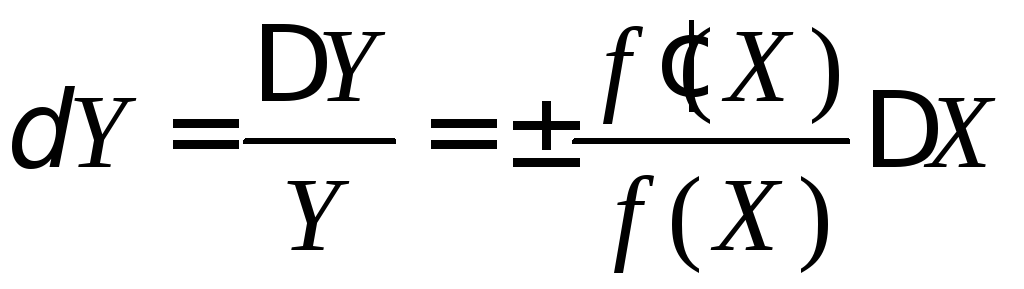. (11)

Якщо посередньо вимірювана величина є функцією кількох аргументів , то повний диференціал цієї функції може бути представлений у такому вигляді:

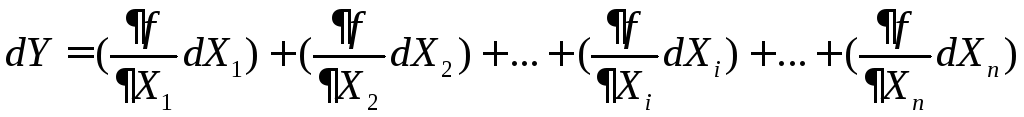. (12)

Цей вираз складається із суми частинних диференціалів, кожний з яких визначає ту частину похибки у величині функції, яка виникає через похибку кожного з аргументів . При обчисленні частинної похідноївсі аргументи, крім, вважаються сталими, а за величиноюдиференціювання здійснюють за правилами, які використовують при диференціюванні функцій однієї змінної. Замінивши у формулі (12)символна, одержимо формулу, яку використовують для визначення абсолютного значення абсолютної похибки функції, що залежить від декількох змінних:

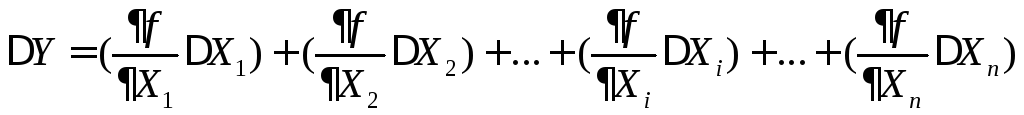. (13)

Абсолютна похибка будь якого аргументу може бути як додатною, так і від’ємною. У залежності від поєднання знаків усіх похибок аргументів за однакових усіх інших умов абсолютне значення абсолютної похибки може мати різну величину. Для того, щоб бути впевненим у тому, що при самому несприятливому поєднанні знаків похибок аргументівпохибка функції не виходить за межітреба визначити максимальне значення. Таке максимальне значення абсолютної похибки, або, як кажуть, гранична похибка, буде одержана тоді, коли усі доданки суми у формулі (13) будуть додатні. Тому на практиці при проведенні розрахунків абсолютної похибки за формулою (13), беруть не суму частинних диференціалів функції багатьох змінних, а суму абсолютних величин частинних диференціалів незалежно від того, які знаки були одержані у частинних похідних при диференціюванні. Таким чином, формула, яку використовують для визначення абсолютної похибки непрямих вимірювань у тому випадку, коли функція залежить від кількох змінних, має такий вигляд:

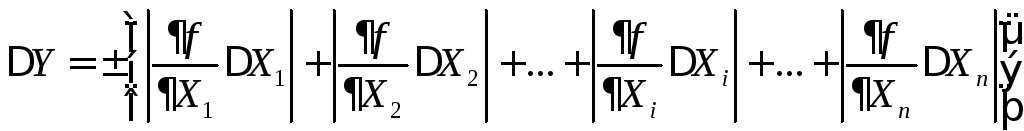. (14)

Наведеною вище формулою (14) зручно користуватися у тому випадку, якщо шукана величина є сумою або різницею результатів прямих вимірювань. Однак дуже часто виникає необхідність визначати похибку за формулами, які відображають складні функціональні залежності. Слід зазначити, що для величин, які виражені формулами, придатними для логарифмування, розрахунок похибок результатів непрямих вимірювань зручніше починати зі знаходження відносної похибки. Оскільки 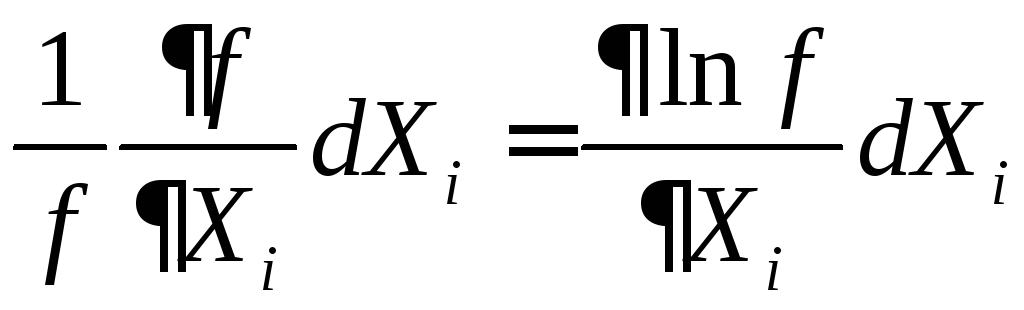, то

. (15)

У цю формулу замість частинних похідних від функції входять частинні похідні від логарифма цієї функції. Тому у тому випадку, коли залежністьвиражена формулою, зручною для логарифмування, простіше спочатку визначити відносну похибку за формулою (16), а потім знайти абсолютну похибку.

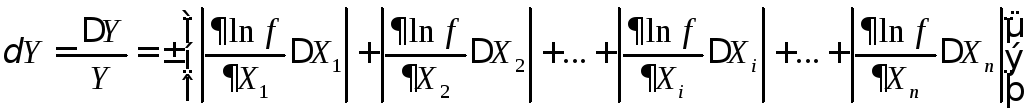. (16)

Таким чином для того, щоб визначити похибку непрямих вимірювань рекомендується такий порядок операцій. Спочатку треба прологарифмувати вихідну функцію, тобто вихідну формулу, за якою розраховують значення досліджуваної фізичної величини, а потім продиференціювати одержаний вираз. Для цього треба спочатку визначити частинні похідні за кожним з аргументів , а потім записати вираз для повного диференціалу логарифма даної функції. У остаточному виразі, за яким буде здійснюватись розрахунок абсолютної похибки, треба замінити символи диференціала, які стоять біля диференціалів усіх аргументівна символ, який позначає абсолютну похибку, з якою було експериментально визначене чи взяте з довідкових таблиць значення даного аргументу. Для того, щоб визначити максимальне значення похибки, яка може бути одержана при найменш придатних умовах проведення даного експерименту, усі знаки «–» у цій формулі, які утворились у результаті логарифмування і диференціювання вихідного виразу, треба замінити на знаки «+». Після цього треба здійснити розрахунок відносної похибки. Для цього необхідно підставити у остаточну формулу для визначення величиниусі відомі значення фізичних величин, які були одержані при проведенні прямих вимірювань чи взяті з таблиць, а також значення їх абсолютних похибок. Зверніть увагу на те, що у випадку проведення серії прямих вимірювань у цю формулу підставляють тільки середні значення величин, а розрахунок значення величини, одержаної у результаті проведення непрямого вимірювання, виконують тільки один раз. Після розрахунку відносної похибкифізичної величини(у відносних одиницях, а не у відсотках) треба визначити абсолютну похибкуза формулоюі записати результат непрямого вимірювання фізичної величиниу такому вигляді

. (17)

Приклади виведення формул для знаходження похибок непрямих вимірювань наведені у додатку №3.