Деякі математичні формули. Логарифмічна функція та її властивості.

a^b = c=> log_a c = b

Основна логарифмічна тотожність:

a^{log a N} = N

Властивості логарифмічної функції: log a (N1N2)= loga N1 + loga N2 log a (N1 / N2)= loga N1 -loga N2 log a (Nm)=m . log a N log a = loga N / k log a b= loga c=>b = c	Логарифмічні тотожності: log a b=1 /logb a log a b .logb a=1 log a N= logak Nk log an N= loga N / n log a 1 = 0log a a = 1
Формула, яка використовується для здійснення переходу від однієї основи логарифму до іншої: log a N= logb N /logb a log 10 N= lgNloge N= lnN

Таблиця диференціалів.

d(C)x = 0, C-const d(kx+b)x = k dx d(xr)x = r xr-1 dx d(ex)x = ex dx d(ax)x = ax ln a dx d(ln x)x = d(log x)x = d(sin x)x = cos x dx d(cos x )x = – sin x dx

d(tg x)x = d(ctg x)x = – d(arcsin x)x = d(arccos x )x = – d(arctg x)x = d(arcctg x)x = –

Основні формули диференціювання.

d(u±υ) = du ± dυ

d(Cu) = Cdu

d(uυ) = du υ + u dυ

d(u/υ) = (du υ – u dυ)/υ²

Формула, за якою здійснюють диференціювання складної функції.

df(h(g(x)))_x = df(h(g(x)))_h(g(x)) dh(g(x))_g(x) dg(x)_x dx

Додаток №3

Приклади розрахунку

відносної та абсолютної похибок непрямих вимірювань

Приклад №1.

I. Робоча формула, яка використовується для розрахунку прискорення сили тяжіння земного за періодом коливань математичного маятника, має такий вигляд:

. (1)

ІІ. Результати прямих експериментальних вимірювань та табличні значення величин, виражені у одиницях СГС є такими.

Нехай - довжина маятника, яка виміряна з абсолютною похибкою. Період коливань маятника, а. Якщо при підрахунках взяти число, то. Розрахунок прискорення сили земного тяжіння за формулою (1) і за даними, одержаними з таблиць та шляхом проведення прямих вимірювань, дав таке його значення:

(2)

ІII. Алгоритм знаходження відносної та абсолютної похибки для робочої формули (1):

(3)

Для того, щоб одержати робочу формулу, за якою можна розраховувати абсолютне значення відносної похибки визначення прискорення сили земного тяжіння , діємо згідно з вказівками викладеними у п. 3 Вступного заняття. Замінимо у чисельниках виразів, які входять у формулу (3) повного диференціала логарифму, символи диференціалуна символи абсолютної похибкиі знак «-« , що стоїть перед третім доданком на знак «+». Таким чином, остаточна формула для визначення абсолютного значення відносної похибки прискорення сили земного тяжіння має такий вигляд:

. (4)

Для проведення розрахунку за формулою (4) у неї треба підставити числові значення всіх величин, що входять до цього виразу, а також абсолютні значення їх абсолютних похибок . Таким чином

(5)

Визначаємо абсолютну похибку визначення прискорення сили земного тяжіння.

(6)

Записуємо остаточний результат визначення прискорення сили земного тяжіння за даними непрямих вимірювань у такому вигляді:.

Приклад№2.

І. Робоча формула, яка служить для визначення в’язкості рідини має такий вигляд:

, де

ІІ. Результати прямих експериментальних вимірювань та табличні значення величин, виражені у одиницях СГС:

ρ= 11,3 г/см³∆ρ= 0,05 г/см³(половина відомого порядку),

ρ₀= 1,26 г/см³∆ρ₀= 0,005 г/см³( – / – / – / – / – / – /– / – / – /–),

g= 9,8 м/с²∆g= 0,02 м/с²(знаючи, що g = 9,81м/с²),

d= 0,196 см ∆d= 0,0005 см(половина ціни поділки мікрометра),

D= 5,6 см ∆D= 0,05 см(половина ціни поділки лінійки),

l= 14,1 см ∆l= 0,05 см( – / – / – / – / – / – /– / – / –/ – /– ),

t= 3,2 c ∆t= 0,2 c(ціна поділки механічного секундоміра).

ІІІ. Алгоритм розрахунку відносної похибки для .

1.Логарифмуємо вираз за натуральним логарифмом:

.

2.Диференціюємо отриманий вираз:

.

3.Замінюємо символ „d” на символ „∆” в чисельниках дробів та знак „–” на знак „+” між доданками:

.(1)

4.Підставляємо у формулу (1) чисельні значення:

.

ІV. Знаходження відносної та абсолютної похибок для робочої формули:

1.

.

2.

.

3.

4.Враховуючи знайдене значення,знайдемо відносну похибку:

.

V. Обчислимо чисельне значення η_і та абсолютну похибку:

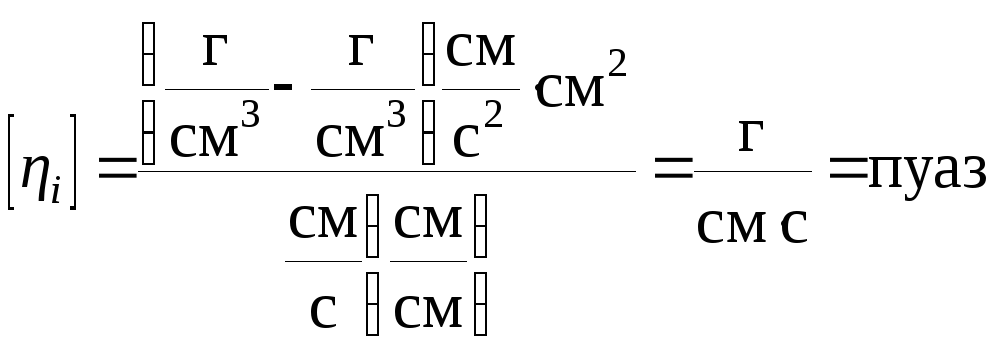,пуаз,

пуаз.

VI. Остаточно запишемо результат у такому вигляді:

пуаз; .

Додаток №4