6) Политропические процессы. Уравнения политропы для идеального газа

Политропическим называется процесс, в котором теплоемкость остается постоянной: С = const. Для идеального газа

CdT = Cv dT + vRT/V dV. Если Сv = const, то отсюда следует PV^n = const. Число n = 1 - vR/(C - Cv) = (C -Cp)/(C - Cv) называется показателем политропы. Примеры политропических процессов:

Адиабатический: C = 0, n = гамма. Изобарический: C = Cp, n = 0. Изохорический: C = Cv, n = беск. Изотермический: C = беск, n = 1.

(В случае изобарического и изохорического процессов предполагается соответственно Ср = const и Сv = const).

Уравнения политропы для газа Ван-дер-Ваальса

P(V,T) = RT/(V-b)-a/V^2, U(V,T) = C_V T - a/V;

дельта Q = C dT

дельта Q = dU + PdV

dU = C_V dT + a/V^2 dV

C_V dT + a/V^2 dV + RT/(V-b) dV - a/V^2 dV = СdT

(C - C_v)dT/T = R dV / (V - b)

(C - C_v)ln (T2/T1) = R ln ((V2 - b)/(V1 - b))

(T2^((C - C_v)/R))/(V2-b) = (T1^((C - C_v)/R))/(V1-b)

T = (P + a/V^2)(V - b)/R

(P + a/V^2)^((C - C_v)/R) (V - b)^((C - C_v)/R - 1) = const

(P + a/V^2)(V - b)^((C - C_v - R)/(C - C_v)) = const - уравнение политропы для газа Ван-дер-Ваальса.

7) Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством.

Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна^[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы^[3].

Адиабата Пуассона[править | править исходный текст]

Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением^[6][15][16]

где — его объём, — показатель адиабаты,  и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

График адиабаты (жирная линия) на диаграмме для газа. — давление газа; — объём.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

где — абсолютная температура газа. Или к виду

Поскольку  всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении ) газ нагревается ( возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент .

Вывод уравнения[править | править исходный текст]

Согласно закону Менделеева — Клапейрона^[6] для идеального газа справедливо соотношение

где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обеих частей уравнения, полагая независимыми термодинамическими переменными , получаем

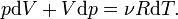
(3)

Если в (3) подставить  из (2), а затем  из (1), получим

или, введя коэффициент :

.

Это уравнение можно переписать в виде

что после интегрирования даёт:

.

Потенцируя, получаем окончательно:

что и является уравнением адиабатического процесса для идеального газа.