§ Примеры вычисления производных от неявных функций.

1⁰.Задано равенство:ln(x²+y²) =arctg. Определяет ли это равенство функцию, и, если – да, то найти.

Определим F(x,y) =ln(x²+y²) –arctg= 0. Для нее якобиан J=существует везде кроме (0, 0), и точек, в которыхи равен:

J===–=0 .

Дифференцируем функцию F(x,y) поx, считаяyфункцией.

== 0;

Тогда: (существует еслиx2y ).

Если уравнение ещё раз продифференцировать по x, то получим:



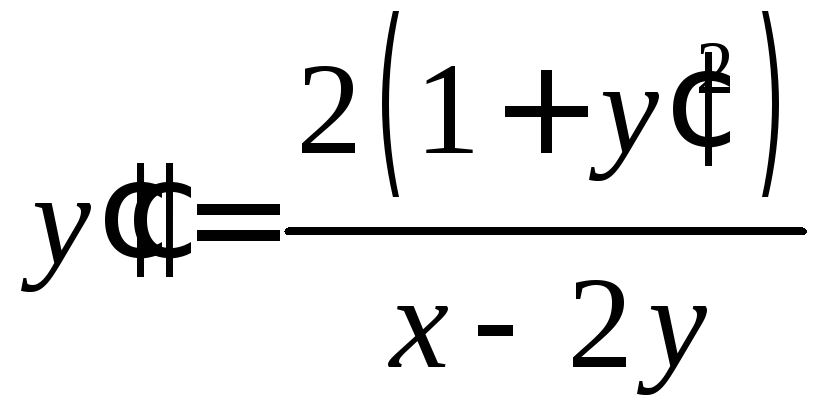 , если.

2⁰.Исследовать на экстремум функциюy=y(x), заданную уравнением:

x³+y³– 3xy= 0.

Дифференцируем равенство по x, считая что, при этомy=y(x):.– необходимое условие экстремума.

а.x= 0;y= 0.б.x = ;y= .

В точке (0,0) j == 3y²– 3x= 0 и, поэтому мы не можем утверждать, что исходное уравнение определяетyкак функцию отx.

В точке x= ,y= найдем.

 дифференцируем

.

В стационарной точке , поэтому=.

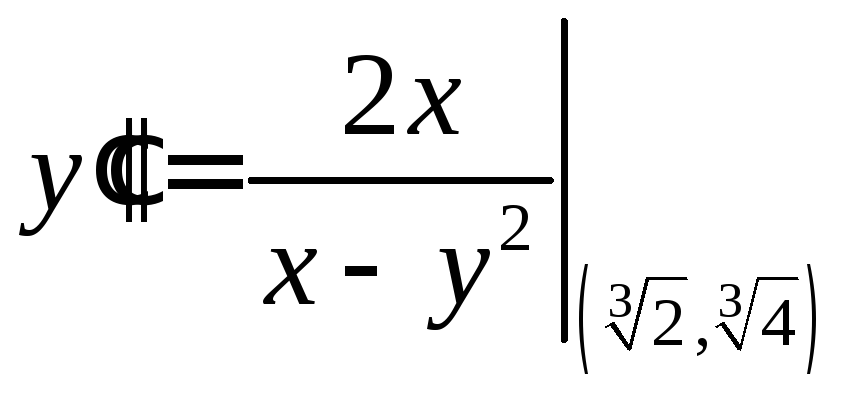Значит, в точке (,) – функцияy=y(x) имеет максимум.

§. Замена переменных в дифференциальных выражениях.

Решение задачи о замене переменных в дифференциальных выражениях посмотрим на примерах.

1. В дифференциальном уравнении сделать замену независимых переменных , и получившееся уравнение решить.

Δ. По формулам дифференцирования сложных функций запишем:

;

.

Решаем получившуюся систему двух уравнений относительно и:

и.

Подставим найденные ив исходное уравнение:

.

После раскрытия скобок и приведения подобных членов получаем уравнение

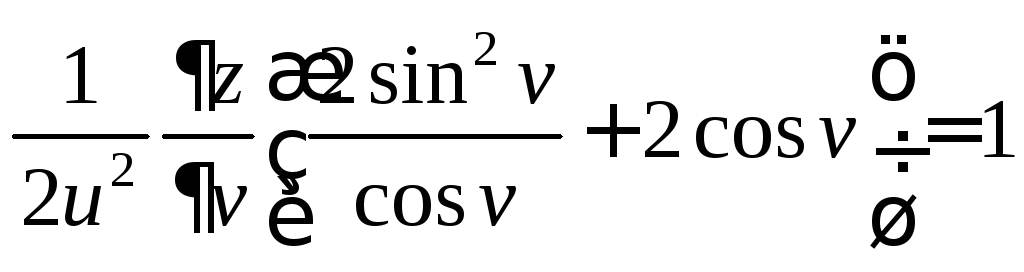
, где–произвольная функция одного переменного. Возврат к старым переменным труда не представляет. ▲

2. В дифференциальном уравнениизаменить независимые переменныеx иy наu иv, а искомую функциюzнаw, если:

.

Δ ==

= .

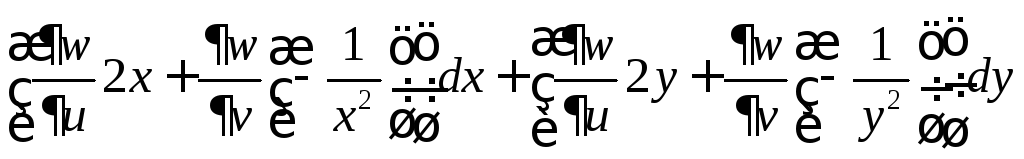С другой стороны, учитывая что , получаем.

Сравнивая два выражения для , получим:

;.

Первое равенство умножим на , а второе наи сложим. Тогда:

. Учтем, что левая часть равенства равна нулю (это исходное уравнение). ▲

3. В выражении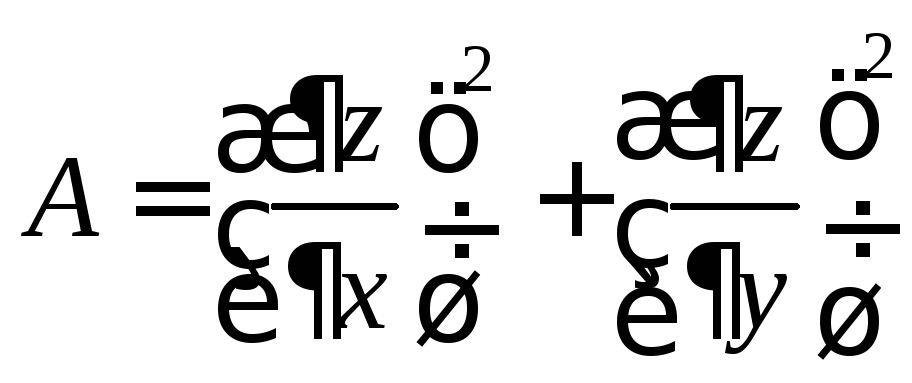сделать замену переменных.

Δ. Прежде всего, отметим что и

;.

Тогда: или, что то же самое,

.

Значит:



; .

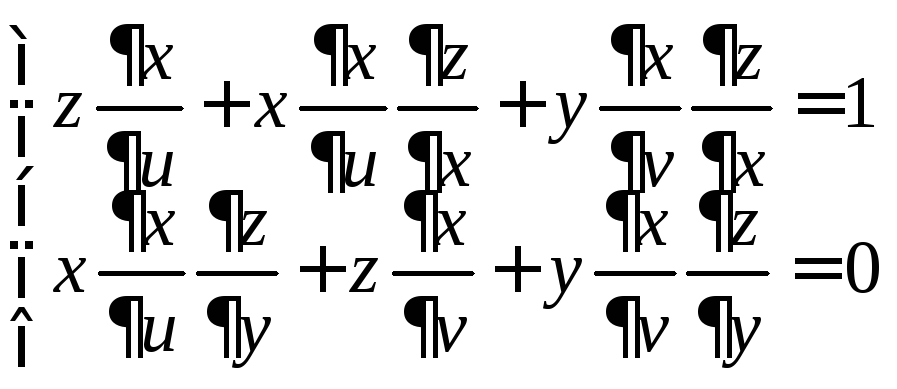
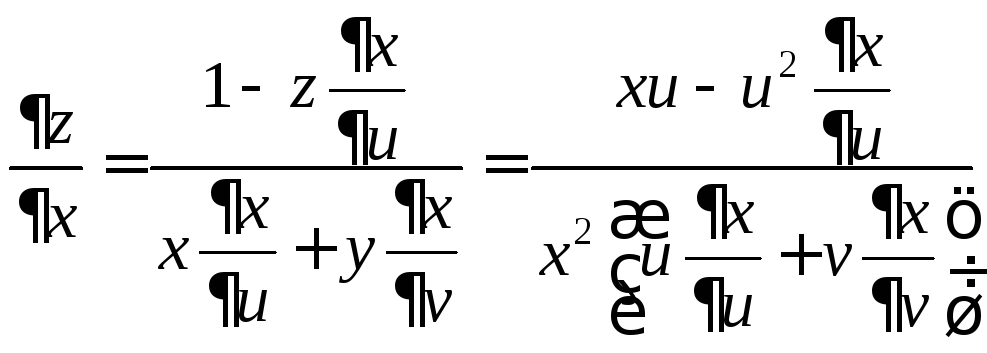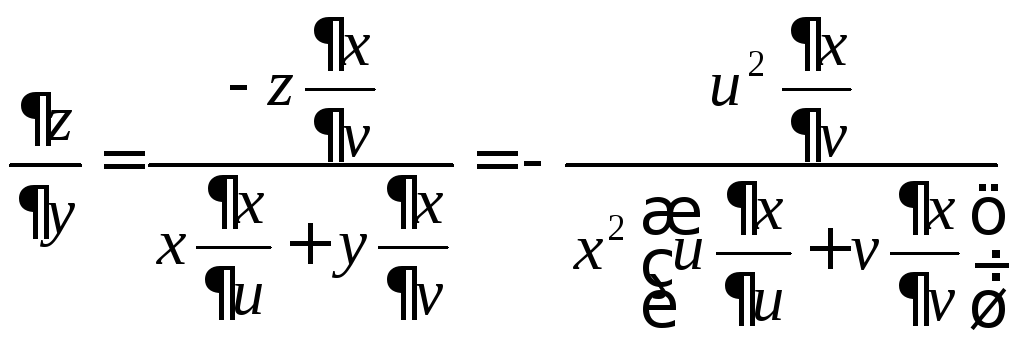И, наконец:

.▲

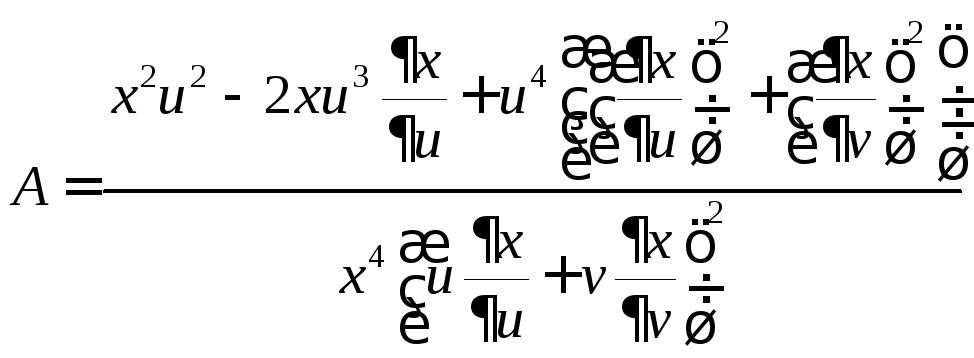§. Условные экстремумы функций многих переменных. Метод неопределенных множителей Лагранжа.

Постановка задачи: Требуется найти экстремумы функции

в предположении, что аргументы функции подчиняются mуравнениям связи:

(*)

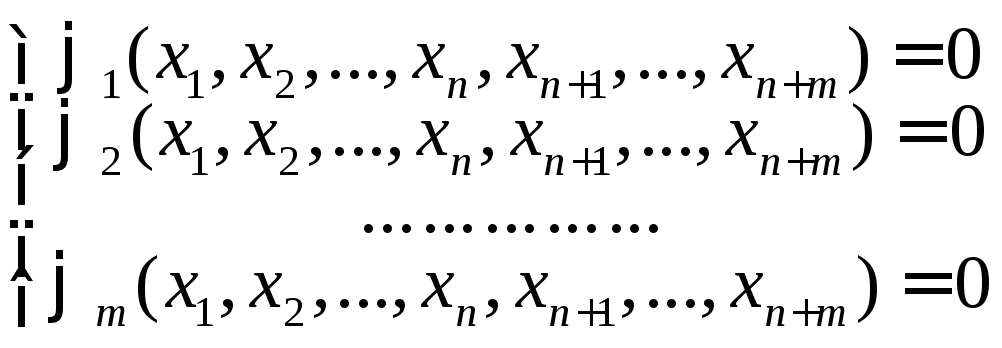Def. Функцияимеет условный экстремум в, удовлетворяющей условиям связи (*), если в некоторой окрестности точкиM₀ для всех ее точек удовлетворяющих уравнениям связи (*) выполняется неравенство:

(для максимума),

(для минимума).

Мы уже, по сути, решали такую задачу, когда из уравнений связи можно было найти отдельные переменные и, в последующем, исключать их из рассмотрения. В общем случае это удается сделать далеко не всегда.

Лагранж предложил метод нахождения экстремума функции , при наличии условий связи:, где.

Cоставим функцию (называемую функцией Лагранжа) :

;

*). Необходимые условия условного экстремума функциис условиями связи (*) совпадаютcнеобходимыми условиями экстремума (обычного) функции.

т.е. ;.

*).Достаточные условия условного экстремума функцииэто достаточные условия экстремума функциигде– значения параметров в критической точке, т.е. фиксированы.

Пример:

1. Найти экстремум функции , если.

Мы уже рассматривали эту задачу ранее и, при этом, выражали через. Если это невозможно сделать, выход из положения предлагает метод неопределенных множителей Лагранжа.

Составим функцию Лагранжа для решения задачи на условный экстремум

.

Условный экстремум функции совпадает с обычным экстремумом функции Лагранжа.

Необходимые условия экстремума



.

Решая эту систему, найдем стационарные точки1).и

2). .

В каждой из этих точек модифицируем функцию Лагранжа, подставляя соответствующее значение и проверим достаточные условия экстремума, составляя в найденных точках соответствующие матрицы из вторых производных.

1).

2).

Учитывая что

, запишем матрицы из вторых производных для каждой из стационарных точек и проверим достаточные условия экстремума

1). .. Экстремума нет.

2). .. Экстремума нет.

ВыводДанная функция условных экстремумов не имеет.

2. Найти экстремум функции, если.

На первом этаперешения задачи составим функцию Лагранжа:

.

Необходимые условия экстремума этой функции имеют вид:

;;;.

Из первых трех уравнений следует, что:

.

Подставляя в четвертое уравнение, находим x, а затем, из полученных выше соотношений, находими. Получаем две стационарные точки:

.

Далеедля каждой стационарной точки составляем модифицированную функцию Лагранжа. Для точки:

.

Составляя матрицу из вторых производных, получаем: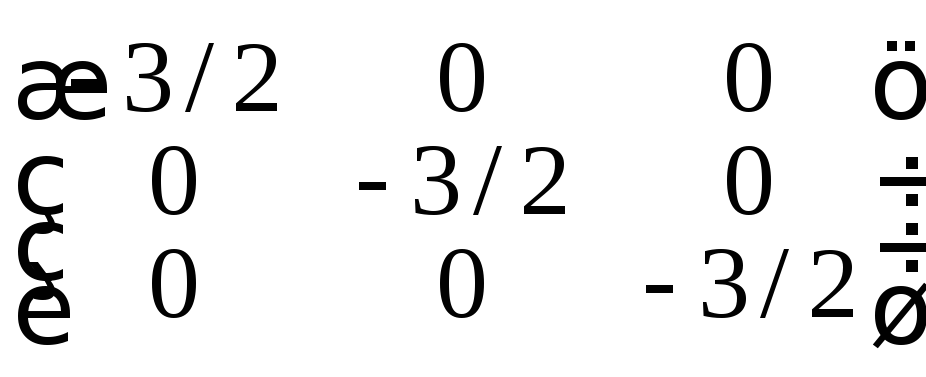. Ее главные миноры чередуются по знаку, начиная с минуса. Следовательно, второй дифференциал модифицированной функции Лагранжа отрицателен и исходная функция в точкеимеет условный максимум.

Для точки :

.

Составляя матрицу из вторых производных, получаем: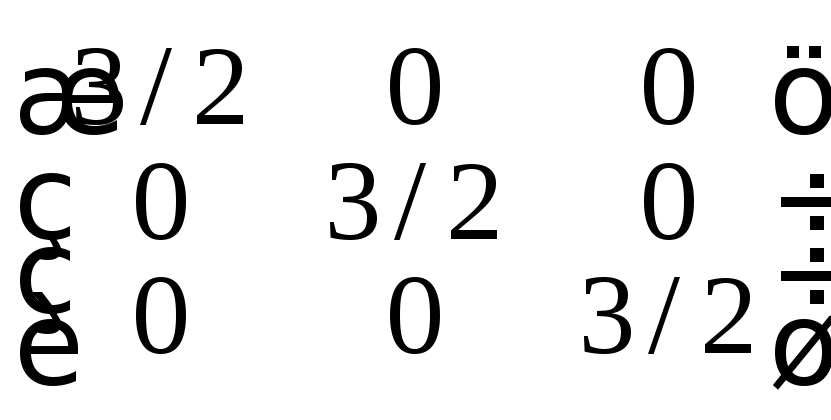. Все ее главные миноры положительны. Следовательно, второй дифференциал модифицированной функции Лагранжа положителен и исходная функция в точкеимеет условный минимум.

2. Найти наибольшее и наименьшее значение функции, при условии.

В этой задаче задано, не ограничение типа «равенство», как в предыдущей, а ограничение типа «неравенство». Поэтому задача решается в два шага.

а). Найдем экстремумы исходной функции в заданной области.

Из необходимых условий экстремума функции следует:

.

Матрица из вторых производных имеет положительные главные миноры, положительный второй дифференциал и, следовательно, минимум в точке (6,–8). Этот факт, однако, нас совершенно не волнует, ибо точка (6,–8) не входит в рассматриваемую область.

б). Найдем теперь наибольшее и наименьшее значения исходной функции на границе области. Т.е. найдем наибольшее и наименьшее значение функциипри условии.

Теперь ограничение типа «неравенство», заменилось на ограничение типа «равенство» и, следовательно, имеем классическую задачу на условный экстремум.

Составляем функцию Лагранжа данной задачи:

.

Необходимые условия экстремума:

.

Находя из этих соотношений , получаем две стационарные точки:и. Безусловно, можно установить характер экстремума в этих точках, однако, для нахождения наибольшего и наименьшего значения функции в этом нет никакой необходимости. Достаточно просто вычислить значения функциив найденных точках. Получаеми.

3. Найти экстремум функции, при условии:

и область изменения переменных:x> 0,y> 0,z> 0,t> 0.

а).Функция Лагранжа:.

б).Необходимые условия экстремума функции Лагранжа:

; ;;;.

Отсюда: .

в) Преобразуем функцию Лагранжа, зафиксировав .

.

г).Для функциипостроим матрицу из вторых производных в окрестности точки: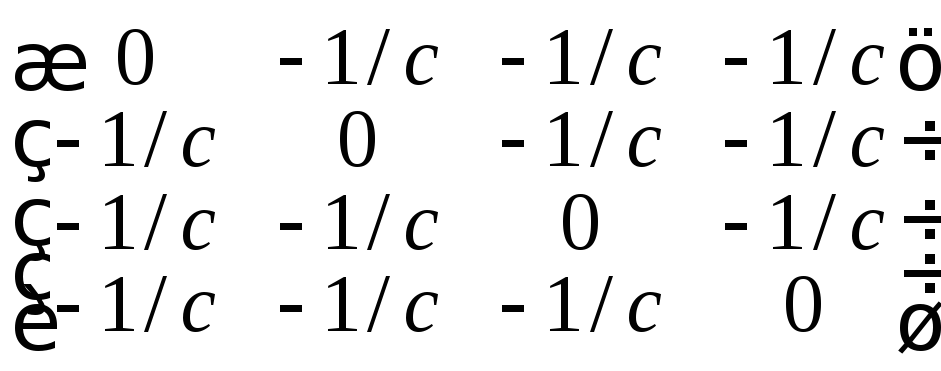и, т.к.₁= 0 то критерий Сильвестра ответа на вопрос о экстремуме не дает. При этом:

.

Находя дифференциал из уравнения связи, получаем:, что

в окрестности особой точки равно: . Подставляяв, получаем:

==

= =.

Ясно, что представляет собой положительно определенную квадратичную форму.

В точке исходная функцияимеет условный минимум.

4. Исследовать на наибольшее и наименьшее значение функцию:

, при условии.

а).Функция Лагранжа:

б).Необходимые условия экстремума функции Лагранжа:

;;

;.

в).Решения этой системы:

*1. ; *2.;

*3. ; *4.;

*5. ; *6..

*7. Если , то должны одновременно выполняться равенства:

;;, что невозможно. Вычисляя значения функции в найденных точках, находим наибольшее и наименьшее ее значения, при условии.

Обращаем внимание на то, что устанавливать имеется ли в критических точках экстремум, и каков характер этого экстремума (т.е. проверять достаточные условия) при решении задачи о наибольшем и наименьшем значении функции нет никакой необходимости.