Криволинейные и поверхностные интегралы

В поверхностном интеграле второго рода часто обозначают

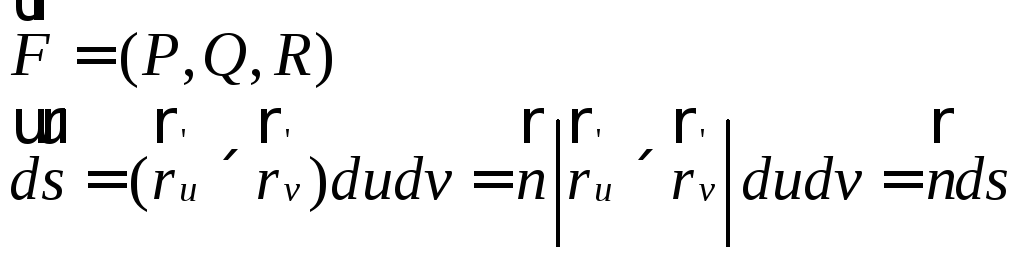где .

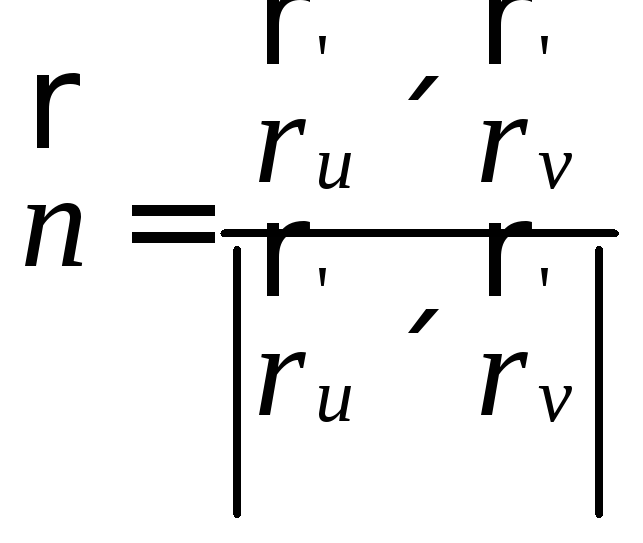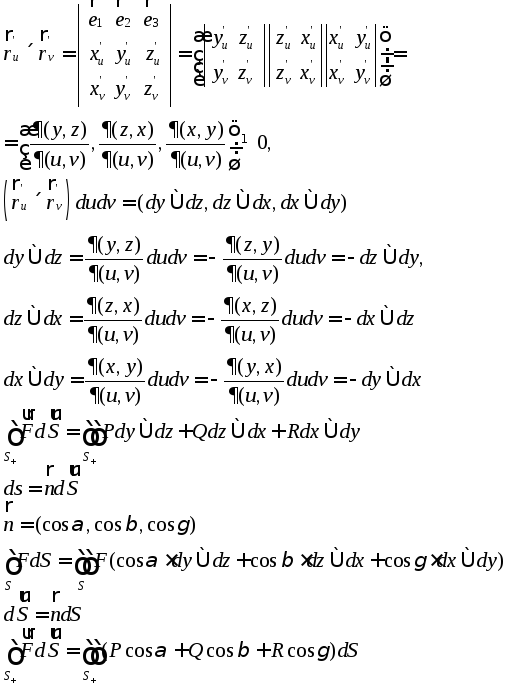
Общая формула Стокса −формула Ньютона-Лейбница-Грина-Остроградского-Гаусса-Стокса-Пуанкаре

где -дифференциальная ()-форма,-внешний дифференциал формы,-многообразие (можно цепь ) размерностис краем –многообразием(соответственно цепью ) размерности.

Формула Ньютона-Лейбница: криволинейный интеграл второго рода вдоль кусочно-гладкой ориентированной кривой с началом в точке и концом в точкеот градиента числового поля ,непрерывно дифференцируемого на этой кривой, равен разности значений поля в конечной и в начальной точках

Функция называется непрерывно дифференцируемой на кривой,если она непрерывно дифференцируема в некоторой окрестности носителя этой кривой.

То же самое , записанное в координатной форме , криволинейный интеграл второго рода вдоль кусочно-гладкой ориентированной кривой с началом в точке и концом в точкеот дифференциала непрерывно дифференцируемой на этой кривой функции, равен разности её значений в конечной и начальной точках:

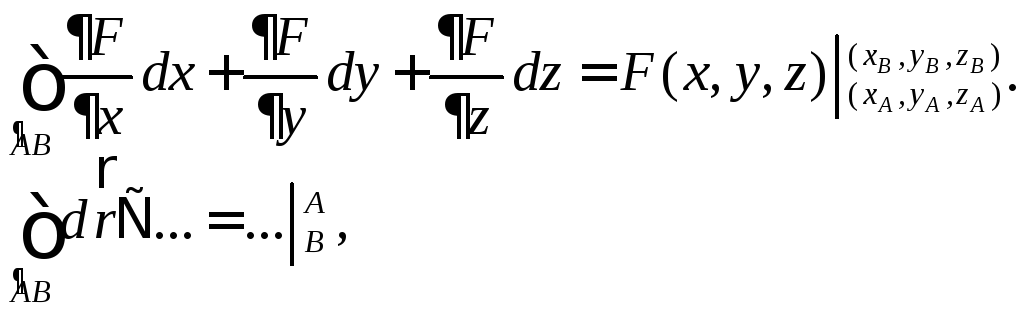
где вместо многоточия можно подставить тензорнозначную ф-ю непрерывно дифференцируемую на кривой , т.е. в некоторой окрестности этой кривой .

Геометрическое определение градиента : проекция на фиксированный орт градиентав точкескалярной ф-и,непрерывно дифференцируемой в некоторой окрестности точки,равная пределу отношения разности значения этой ф-ии на концах произвольного отрезка прямой, проходящего вдоль направления ортачерез точкуи содержащегося в указанной окрестности , к длине этого отрезкакогда диаметр отрезка стремится к нулю

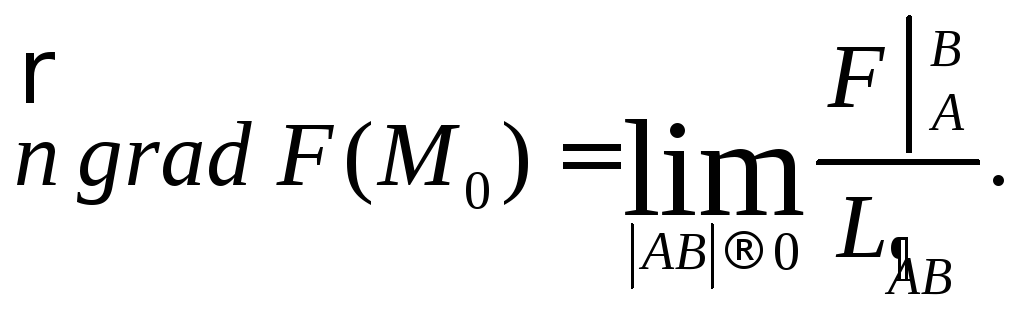
Формула Остроградского-Гаусса: интеграл по объёму ,ограниченному замкнутой кусочно-гладкой ориентируемой поверхностью, от дивергенции векторного поля, непрерывно дифференцируемого на замыкании этого объёма, т.е. на объеме вместе с краем, равен потоку поля через поверхность, ограничивающую объём, и ориентированную внешней нормалью

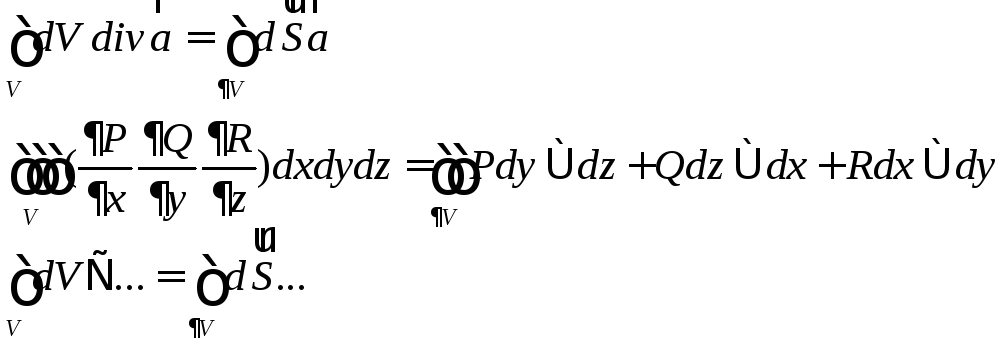
Геометрическое определение дивергенции

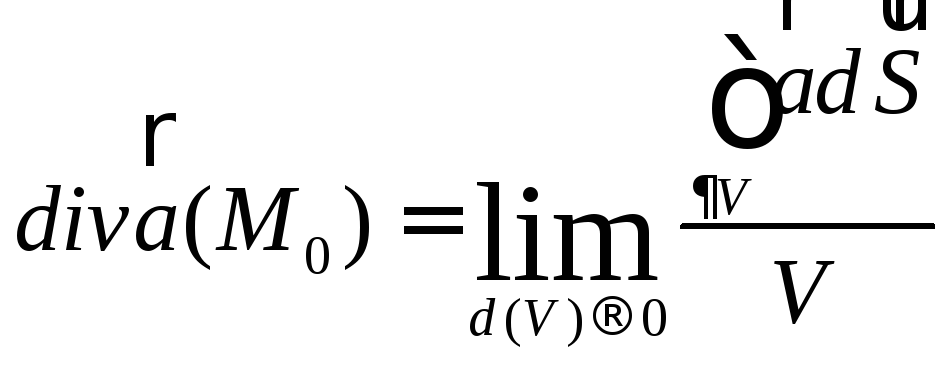
Формула Стокса: поток ротора векторного поля через кусочно-гладкую ориентированную поверхность с кусочно-гладким краем ,ориентированным так , что с конца ориентирующего вектора нормали к поверхности обход края в положительном направлении выглядит происходящим против часовой стрелки ,равен циркуляции этого вектора по краю поверхности

предполагается, что компоненты поля и их производные ,встречающиеся в роторе , непрерывны на поверхности вместе с краем, т.е. в некоторой окрестности этого множества.

В координатной записи формулы Стокса ,для сокращения записи, знак внешнего умножения часто подразумевают, но не пишут.