§. Криволинейные интегралы 2го рода.

Def :Пусть вЕ₃задана вектор-функция,и при этомx(t),y(t),z(t)C_[a,b],C¹_[a,b], т.е. вЕ₃задана гладкая криваяL.

Пусть на кривой Lзадана векторная функция:

.

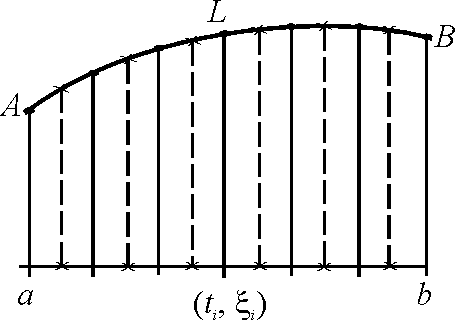
Рассмотрим промежуток [a,b] изменения параметраt , и на [a,b] зададим разбиениеPс отмеченными точками ξ, т.е. зададим (P,ξ). Разбиение (Р,ξ) отрезка [a,b] индуцирует разбиение кривойLс отмеченными точками. И рассмотрим:

.

Если такой предел существует, то он называется криволинейным интегралом 2^города и обозначается:.

Геометрический смысл криволинейного интеграла 2^города – работа силового полявдоль кривойL.

1⁰. Если ,и при этомx(t),y(t),z(t)C_[a,b],C¹_[a,b],

=

= .

Эта формула дает способ вычисления криволинейного интеграла 2^города сведением к интегралу Римана, и следует из определения, в котором в левой части фактически записана интегральная сумма для интеграла стоящего в правой части.

2⁰. Формула для вычисления криволинейного интеграла 2^-города:

.

Здесь – единичный вектор касательной к кривой, а– его направляющие косинусы.

3⁰. .

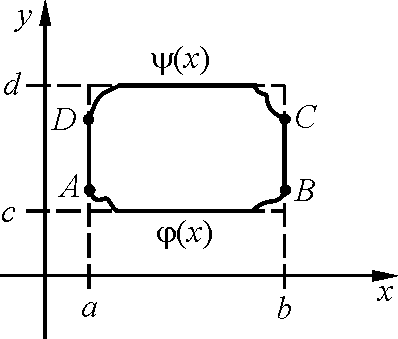
4⁰. Формула Грина.ПустьG– плоская область и γ – кусочногладкий контур, являющийся границей областиG. Пусть взаданыP(x,y) иQ(x,y), непрерывные вGвместе си. Тогда: .

З

амечание:γ⁺- означает, что контур γ проходится в положительном направлении – т.е. против часовой стрелки (при обходе контура левая рука все время находится в области.

Δ. Рассмотрим:

= .

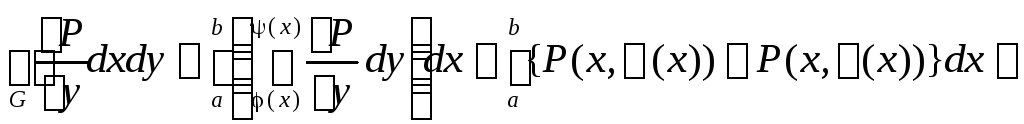
Здесь учтено, что интегралы иравны нулю из-за того, что на промежуткахBCиDA.

Таким образом: =. Аналогично: =.

После сложения двух полученных формул, получаем доказываемую формулу. ▲

Примеры :

1⁰.Вычислить, если криваяLсоединяет точки от (0,0) до (1,1).

a.y =x;б.y =x²;в.x =y².

а). J = .

б). J= .

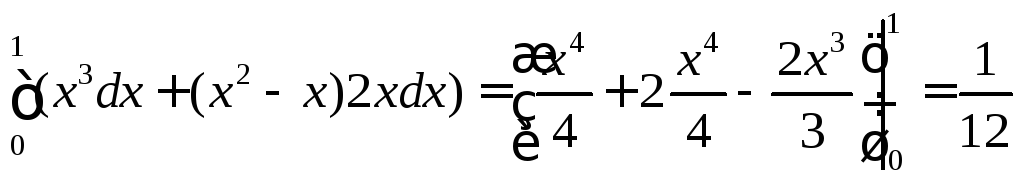в). J =.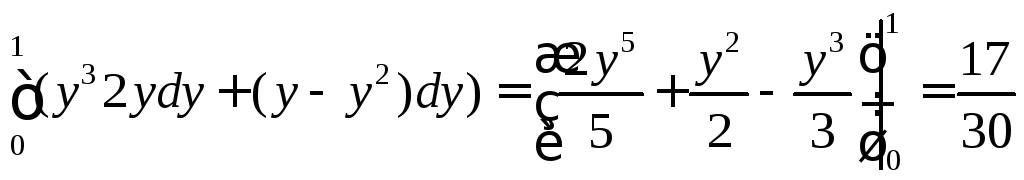

Выясняется, что интегралы получаются разные, т.е. значение интеграла зависит не только от начальной и конечной точек кривой, но и от самой кривой L.

2⁰. Вычислитьвдоль тех же кривых, что и в предыдущей задаче.

a)J = . б)J= .

в) J= .

а в данной задаче на всех трех исследованных путях результат один и тот же. Это не означает, что и на других путях так будет, но…

г) Рассмотрим J=.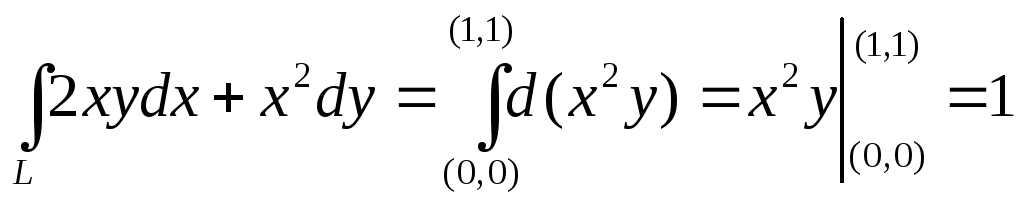

Проведенная выкладка показывает, что интеграл действительно не зависит от пути интегрирования (здесь нет никакого конкретного пути), а зависит только от начальной и конечной точки дуги.

Когда же будет наблюдаться такое явление?

§. Условия независимости криволинейного интеграла 2го рода от пути интегрирования.

Т⁰.Пусть функцииP(x,y,z),Q(x,y,z),R(x,y,z) определены и непрерывны в

области G, лежащей на гладкой поверхностиS, и γ – граница областиG.

Тогда эквивалентны следующие условия:

A^*). Для любого замкнутого контура γ вG ;

B^*). Для любыхA,BєGне зависит от кривой, соединяющей

точки AиB, и лежащей в областиG;

С^*). ВыражениеPdx+Qdy+RdzвGявляется полным дифференциалом

некоторой функции U(x,y,z), т.е.U=U(x,y,z) такая,чтоdU=Pdx+Qdy+Rdz;

D^*). Для функцийP(x,y,z),Q(x,y,z),R(x,y,z) в областиGвыполняются условия:

; ; .

При этом : (*)

Последнюю формулу можно назвать формулой Ньютона-Лейбница для криволинейных интегралов.

Замечание 1.(связь А^*и В^*).не зависит от кривойL, соединяющей точкиАиВ.

Замечание 2.(связь С^*иD^*).