Раздел 1. ОпределЕнный интеграл § Основная задача интегрального исчисления – нахождение площади криволинейной трапеции

П

остановка задачи:Найти площадь фигуры, ограниченной снизу замкнутым промежутком оси абсциссI = [a,b] (y= 0), слева – вертикальной прямойx =a, справа – вертикальной прямойx=bи сверху – дугой графика функцииy=f (x). Такая фигура называется криволинейной трапецией опирающейся на промежутокI .

Несколько слов о понятии площади. Студенты с большим трудом и невнятно формулируют понятие площади. И не мудрено. В программе школьного образования не формулируется понятие площади, и оно остается чисто интуитивным. На самом деле площадь это некоторая функция , заданная на геометрических объектахи такая, что1)и 2).

Теперь займемся решением поставленной задачи. Для этого поступим следующим образом:

А.Разобьём промежутокIнаnчастей, не обязательно равных по длине, точками:

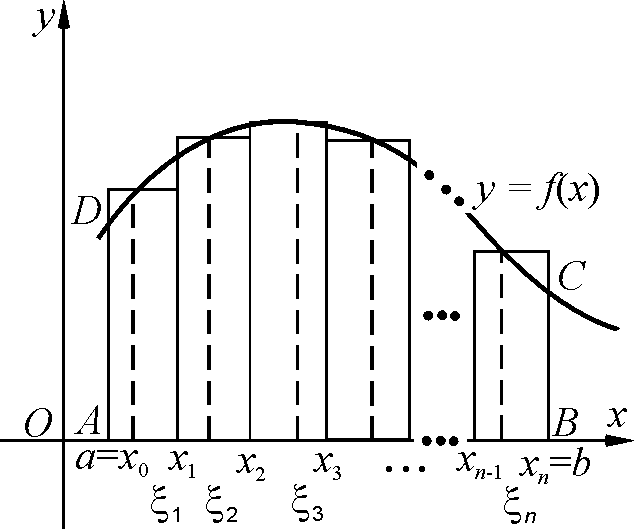
, и обозначим

– промежутки разбиения. Величинуназовем диаметром промежутка разбиения, а величину– мерой промежутка разбиения.

При этом: и

. Для интервала понятие меры и диаметра не отличаются. Для произвольного множества самое большое из расстояний между элементами множеств, конечно, не всегда не совпадает с суммарной длиной интервалов, его составляющих.

Пусть – внутренность промежутка разбиения:=() т.е.. При этом говорят: Задано разбиениеР =промежуткаI= [a,b], а величинаназывается параметром разбиенияР.

Б.Теперь для каждоговыберем точкит.е..

П

олучаемразбиение с отмеченными точками.

В.Построим сумму площадей образовавшихся прямоугольников:, и перейдем к пределу при параметре разбиения, стремящемся к нулю. Если такой предел существует, то он называется определенным интегралом от функциипо промежуткуи для неотрицательной функцииявляется площадью криволинейной трапеции.

.

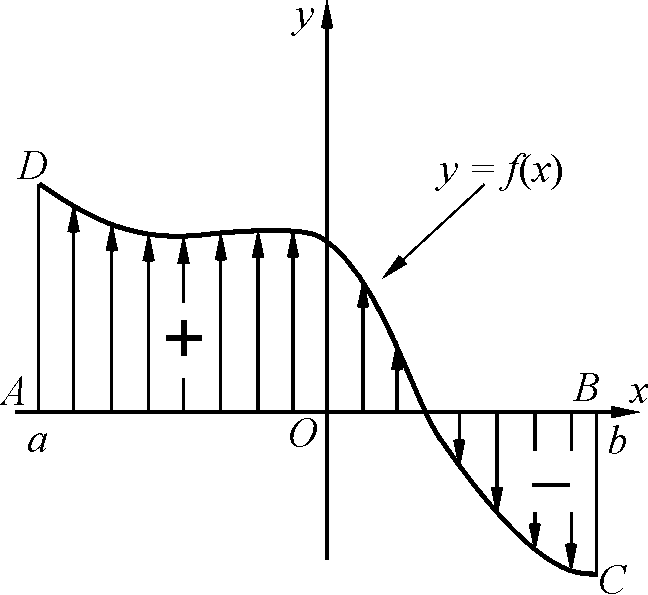
Если функция является знакопеременной то определенный интеграл это, вообще говоря, не площадь а ориентированная площадь, когда считается, что фигуры лежащие выше оси абсцисс имеют положительную площадь, а фигуры лежащие ниже оси абсцисс имеют отрицательную площадь.

§ Свойства разбиений

Говорят, что разбиение Рмельче чем разбиение(иликрупнееР), (илиРследует за) и записывают, если все точки разбиениясодержатся среди точек разбиенияР. Отметим три важных свойства отношения «крупнее – мельче» для разбиений:

а)существуют разбиения со сколь угодным малым параметром:

I= [a,b]. Выбирая;k= 0,1,2,…,n. Тогдаи выбираядостаточно большим, можно сделать параметр разбиения сколь угодно малым.

б)для двух любых разбиенийсуществует третье разбиение, следующее за любым из них:

с) транзитивность отношения «крупнее – мельче»:

и, что то же самоеP₁P₂P₂P₃P₁P₃.

§ Определение определённого интеграла на языке . Предел по базе

Def:ВеличинаI(f ) называется определённым интегралом от функцииf на промежутке [a,b]D(f), если:.

Def:Если в множествеX задана системаB подмножествBмножестваXтакая, что:

а) BBB; б)B₁,B₂BB₃BB₃B₁∩B₂,

то говорят, что в множестве Xзадана база.

Примеры.

1˚. Множество открытых окрестностей точкиа образуют базу. Обозначим эту базуP.

2˚. Множество открытых проколотых окрестностей точкиа образуют базу (P).

3˚. Множество открытых окрестностей точкиа на плоскости образуют базу(P).

4˚. Множество открытых проколотых окрестностей точкиа на плоскости образуют базу(P).

5˚. Множество всех разбиений промежутка [a,b] образуют базу (P)..

6˚. Множество всех разбиений промежутка [a,b] с параметром разбиения_P<образуют базу.

7˚. Множество всех разбиений промежутка [a,b] с отмеченными точками образуют базу.

6˚. Множество всех разбиений промежутка [a,b] с отмеченными точками с параметром разбиения_P<образуют базу. Последние три базы обозначают базуPили.

Def:. Пределом функцииf(x) по базе Bназывается числоА, такое, что:

. и тогда определение определенного интеграла может быть записано через предел по базе разбиений с отмеченными точками с параметром разбиения_P<:.