7.1.3. Співвідношення невизначеностей Гейзенберга

Хвильові властивості мікрочастинок свідчать про обмеженість застосування до них деяких понять, якими характеризуються тіла в класичній механіці. Так, в класичній механіці ми можемо одночасно вказати положен­ня тіла в просторі та його імпульс, що дас змогу вказати просторове положення тіла у наступний момент часу, визначаючи тим самим траєкторію його руху. Для мікро­частинки це стає неможливим. Завжди існують невизна­ченості у значеннях її координати та імпульсу, пов'язані певним співвідношенням, яке було встановлено в 1927 р. німецьким фізиком В. Гейзенбергом:

(7.5)

З цього співвідношення випливає, що чим точніше ми спробуємо визначити координату частинки, тим з меншою точністю зможемо охарактеризувати її імпульс:

Приклад: згідно з класичним уявленням електрон в ато­мі рухається по коловій орбіті зі швидкістюЦю швидкість легко визначити за умови . тобто

Належність електрона до атома потребує, щоб невизна­ченість у значенні його координати відповідала атомним розмірам, тобто тоді із співвідношеннямаємо

Звідси випливає, що невизначеність у значенні швид­кості електрона дорівнює самій швидкості. Таким чином, неможливо зберегти уявлення про орбіту, вздовж якої рухається електрон з визначеною швидкістю, тобто класич­ні уявлення у даному випадку ми не в змозі застосувати.

Аналогічно пов'язані між собою невизначеності енергії частинки і часу її життя в даному енергетичному стані:

(7.6)

а також невизначеності моменту імпульсу та кутової координати.

Наведені співвідношення називаються співвідно­шеннями невшначеностей Гейзенберга. Вони становлять одне з основних положень квантової механіки. Відмова від детермінованого поняття траєкторії руху, притаманного класичній механіці Ньютона-Галілея, і перехід до ймовірносного опису положення мікрочастинок у просторі є однією з істотних і принципових особливостей квантової механіки — науки про мікросвіт.

Цікаво зазначити, що принцип невизначеностей зустрічається і в класичній фізиці, що має своє відображен­ня у такому прикладі. Справді, із формули (7.6) випливає такий зв'язок між невизначеностями частоти і часу вимірюванняякий повністю підтверджується медичною практикою. За малий проміжок часу(скажімо,неможливо точно виміряти частоту серцевих скорочень, тобто невизначеність частоти Ду є дуже великою.

7.1.4. Основне рівняння квантової механіки - рівняння Шредінгера

Рівняння, що описує рух мікрочастинки, мас відтворю­вати її хвильові властивості, тобто повинне бути подібним до хвильового рівняння, що описує поширення оптичних або акустичних хвиль

(7.7)

Ми можемо міркувати таким чином: якщо мікро­частинка, яка рухається, має хвильові властивості і може бути охарактеризована довжиною хвилі, то її стан можна описати за допомогою деякої функції ЧУ, яка задовольняти­ме хвильове рівняння (7.7), тобто

(7.8)

Враховуючи зв'язок між частотою і періодом , а також зв'язок між довжиною хвилі, швидкістю і періодомі формулу для довжини хвилі де Бройля, відношенняможна подати таким чином:

(7.9)

Тоді рівняння набуває такий вигляд:

(7.10)

де - кінетична енергія частинки. Рівняння (7.10) описує одновимірний рух частинки. У випадку, коли частинка рухається в тривимірному просторі, рівняння (7.10) матиме вигляд:

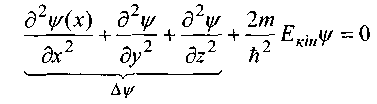(7.11)

або

(7.12)

де - так званий оператор Лапласа, який діє на хвильову функцію і дорівнює сумі всіх других просторових похідних відРівняння (7.12) описує рух вільної частинки.

Якщо частинка рухається в силовому полі, то її повна енергія дорівнює сумі кінетичної та потенціальної енергій: , звідкиУ цьому випадку рівняння (7.12) записується таким чином:

(7.13)

Рівняння (7.13) - стаціонарне рівняння Шредінгера, запропоноване ним у 1926 році.