
4сем / ПП_4_сем_pdf / ПП _11 _Оценки пар расп
.pdf
ПП 11. ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
1. Статистические оценки параметров распределения
Выборка – {X1 , X 2 ,..., X n } - n ─мерная случайная величина.
Статистическая оценка неизвестного параметра теоретического распре-
деления – функция от наблюдаемых случайных величин X1 ,X2 ,...,Xn .
2.Точечные и интервальные оценки. Доверительный интервал, точность оценки, доверительная вероятность (надежность)
Точечная оценка неизвестного параметра Θ ≈Θ* (x1 ,x2 ,...,xn ) – случайная функция Θ* (X1 ,X2 ,...,Xn ), значение которой для любой реализации выборки
принимают за приближенное значение параметра Θ.
Интервальная оценка неизвестного параметра Θ – случайная функция
Θ* (X1 ,X2 ,...,Xn ) такая, что
P (−ε1 < Θ−Θ* (X1 ,X2 ,...,Xn )<ε2 )=γ =1−α ,
или
P(Θ* (X1 ,X2 ,...,Xn )−ε1 <Θ<Θ* (X1 ,X2 ,...,Xn )+ε2 )=1−α ,
т.е., интервал
(Θ* (X1 ,X2 ,...,Xn )−ε1 ,Θ* (X1 ,X2 ,...,Xn )+ε2 )за-
ключает в себе (покрывает) неизвестный параметр Θ с вероятностью γ . Сам интервал носит название доверительного интервала, величина γ =1 −α называется доверительной вероятностью оценки (надежностью, коэффициентом доверия), числа
Θ* (X1 ,X2 ,...,Xn )−ε1
иΘ* (X1 ,X2 ,...,Xn )+ε2
– доверительными границами, α – уровнем значимости (существенности).
Доверительная вероятность характеризует степень доверия к событию (вероятность события), что неизвестный (но не случайный!) параметр Θ содержится внутри доверительного интервала; уровень значимости α характеризует риск наступления события, что параметр Θ в интервале не содержится. Чем более существенны последствия ошибки, что параметр Θ не содержится в доверительном интервале, тем меньшим уровнем значимости нужно задаваться.
1

Если плотность распределения Θ* (X1 ,X2 ,..., Xn ) симметрична относи-
тельно своей медианы, применяют следующий способ получения интервальной оценки:
P (Θ* (X1 , X 2 ,..., X n )− Θ < ε)=γ =1 −α ,
P (Θ* (X1 , X2 ,..., Xn )−ε <Θ<Θ* (X1 , X2 ,..., Xn )+ε)=γ =1 −α ,
т.е. нижняя и верхняя границы доверительного интервала симметричны относительно оценочной функции Θ* (X1 ,X2 ,...,Xn ). Величина ε , характеризующая ширину доверительного интервала, называется точностью оценки.
При несимметричной плотности распределения Θ* (X1 ,X2 ,...,Xn ) для на-
хождения доверительных границ обычно пользуются условиями
P (Θ < Θ* (X1 ,X 2 ,...,X n )−ε1 )= α2 , P (Θ > Θ* (X1 ,X 2 ,...,X n )+ε2 )= α2 .
Точечные оценки проще в вычислении, но не позволяют установить степень достоверности оценки.
Интервальные оценки наряду с возможными границами значений параметра, дают вероятность, с которой истинное (неслучайное!) значение параметра лежит между этими (случайными) границами. Естественно, чем больше надежность оценки, тем шире доверительный интервал, и наоборот, так что практические вычисления являются компромиссом между точностью и надежностью оценки. Наиболее часто задают надежность 0,95; 0,99 и 0,999.
3. Несмещенные, состоятельные и эффективные оценки
Статистическая оценка Θ* называется несмещенной, если ее математическое ожидание равно Θ, т.е. M Θ* = Θ.
Статистическая оценка Θ* называется состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е.
ε > 0 nlim→∞ P (Θ* −Θ < ε)=1.
Из неравенства Чебышева следует, что несмещенная оценка, дисперсия которой стремится к нулю при n → ∞, является состоятельной.
Статистическая оценка Θ* называется эффективной, если при данном объеме выборки из всех возможных оценок она имеет наименьшую дисперсию.
4. Точечная оценка генерального среднего по выборочному среднему
|
|
|
= |
|
X1 + X 2 + ...+ X n |
. |
|
|
|
X B |
|||||
|
|
|
|
||||
|
|
|
|
|
|
n |
|
|
– несмещенная оценка M [X ], |
|
|
– состоятельная оценка M [X ]. |
|||
X B |
|
X B |
|||||
Если случайная величина X распределена нормально, то оценка X B будет и
эффективной.
2
5. Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
|
1 |
n |
||
Выборочная дисперсия DB = |
∑(Xi − |
|
)2 (среднее значение квадрата |
|
X B |
||||
|
n i=1 |
|||
отклонения) является смещенной оценкой генеральной дисперсии. Для получения несмещенной оценки достаточно перейти к исправленной выборочной дисперсии,
|
|
|
|
|
n |
|
|
1 |
n |
|||
|
s2 = |
|
DB = |
∑(Xi − |
|
)2 . |
||||||
|
|
X B |
||||||||||
|
|
n −1 |
|
|||||||||
|
|
|
|
|
|
n −1 i=1 |
||||||
Исправленная выборочная дисперсия является несмещенной и состоя- |
||||||||||||
тельной оценкой генеральной дисперсии. |
||||||||||||
Оценка s2 = |
|
n |
|
D для генеральной совокупности не является эффектив- |
||||||||
n |
−1 |
|||||||||||
|
|
B |
|
|
|
|
|
|||||
ной, но для нормального распределения величины X оценка является асимптотически эффективной, т.е., при n →∞ отношение дисперсии этой оценки к минимально возможной дисперсии оценки стремится к единице.
6. Методы получения точечных оценок параметров распределения
Метод моментов.
Оценка одного параметра. Пусть известен вид плотности распределения f (x,θ ), зависящей от одного параметра θ , но не известно значение этого па-
раметра. Для нахождения оценки этого параметра достаточно составить одно уравнение, например, для начальных моментов первого порядка: xB = M (X ).
Так как математическое ожидание признака генеральной совокупности
∞ |
|
|
|
|
|
|
|
|
|
|
|
M (X )= ∫ x f |
(x,θ)dx =ϕ (θ) зависит от неизвестного параметра θ , |
а выбо- |
|||||||||
−∞ |
|
|
|
|
|
|
|
|
|
|
|
рочное среднее |
x |
B |
= |
x1 + x2 + ... + xn |
зависит от реализации выборки |
x ,x ,...,x , |
|||||
|
|||||||||||
|
|
|
n |
|
|
|
1 |
2 |
n |
||
|
|
|
|
|
x1 + x2 + ... + xn |
|
|
|
|
||
то после решения уравнения |
ϕ (θ)= |
мы |
получаем |
||||||||
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
θ* =ψ (x1 ,x2 ,...,xn ), оценку неизвестного параметра как функцию значений
конкретной выборки.
Оценка двух параметров. Пусть задан вид плотности распределения, зависящей от двух неизвестных параметров, f (x,θ1 ,θ2 ). Для их оценки можно, на-
пример, приравнять начальные моменты первого порядка и центральные моменты второго порядка, т.е.,
|
|
|
1 |
n |
[X ], или M (X )= xB , D (X )= DB . |
αk* [X ]= xk = |
∑(xi )k , µ2* [X ]= µ2 |
||||
|
|
|
n i=1 |
|
|
3
Аналогично случаю одного параметра, теоретические моменты есть функции параметров θ1 ,θ2 , а выборочные моменты зависят от реализации выборки. Ре-
шая полученную систему относительно неизвестных параметров, получаем их точечные оценки:
θ * =ψ |
1 |
(x ,x ,...,x |
n |
), |
θ * =ψ |
2 |
(x ,x ,...,x |
n |
). |
1 |
1 2 |
|
2 |
1 2 |
|
Метод максимального правдоподобия Дискретные случайные величины. Пусть Х – дискретная случайная величи-
на, для которой в результате опыта получена выборка значений x1 ,x2 ,...,xn . Вид
закона распределения известен; закон содержит неизвестный параметр θ , для |
|||||
которого требуется найти точечную оценку на основании данных выборки. |
|||||
Обозначим вероятность P (X = xi )= p (xi ;θ), i |
= 1 , 2 , . .. , n . |
||||
Функцией правдоподобия дискретной случайной величины Х называ- |
|||||
ют функцию аргумента θ и данных выборки x1 ,x2 ,...,xn : |
|||||
|
|
L (x1 ,x2 ,...,xn ;θ)= p (x1 ;θ) p (x2 ;θ) ... p (xn ;θ). |
|||
В качестве |
|
точечной оценки параметра |
θ принимается значение |
||
θ* =θ* (x ,x |
2 |
,...,x |
n |
), при котором функция правдоподобия достигает наиболь- |
|
1 |
|
|
|
||
шего значения. Полученную оценку называют оценкой максимального прав-
доподобия.
При практических вычислениях чаще используют функцию
ln L (x1 ,x2 ,...,xn ;θ)= ln p (x1 ;θ)+ln p (x2 ;θ)+ ...+ln p (xn ;θ),
называемую логарифмической функцией правдоподобия, так как функции L
и ln L достигают максимума при одном и том же значении θ .
Непрерывные случайные величины. Пусть Х – непрерывная случайная величина, для которой в результате опыта получена выборка значений x1 ,x2 ,...,xn .
Вид плотности распределения известен; плотность содержит неизвестный параметр θ , f (x)= f (x,θ), для которого требуется найти точечную оценку на
основании данных выборки.
Функцией правдоподобия непрерывной случайной величины Х назы-
вают функцию аргумента θ и данных выборки x1 ,x2 ,...,xn :
L(x1 ,x2 ,...,xn ;θ) = f (x1 ;θ) f (x2 ;θ) ... f (xn ;θ).
Дальнейшие вычисления аналогичны случаю дискретной случайной величины.
После решения уравнения ddlnθL = 0 , называемого уравнением правдопо-
добия, которое дает критические точки функции правдоподобия, необходимо
отобрать точки максимума, пользуясь условием |
d 2 ln L |
< 0 |
. Полученная точка |
|
dθ2 |
||||
|
|
|
максимума θ* дает оценку максимального правдоподобия параметра θ .
4
Если плотность распределения зависит от двух неизвестных параметров, f (x)= f (x;θ1 ,θ2 ), то и функция правдоподобия является функцией двух пере-
менных, θ1 ,θ2 . Для нахождения критических точек нужно решить систему
∂ln L = 0,
∂θ1
∂ln L = 0,
∂θ2
Для того, чтобы в критической точке достигался максимум, достаточно, чтобы выполнялись условия AC − B2 > 0 , A < 0 (или C < 0 ), где A,B,C – значения вторых производных в критической точке P (θ1 ,θ2 ):
A = |
∂2 ln L |
|
, B = |
∂2 ln L |
|
, C = |
∂2 ln L |
. |
∂x2 |
|
∂x∂y |
|
∂y2 |
||||
|
P |
|
P |
|
P |
|||
|
|
|
|
|
|
|||
|
7. Интервальные оценки |
|
||||||
При получении точечной оценки необходимо знать лишь выражение для оценки Θ* (X1 ,X2 ,...,Xn ) как функцию данных выборки, а для получения интервальной оценки необходимо также знать закон распределения Θ* (X1 ,X2 ,...,Xn ), с помощью которого рассчитывается вероятность, вид гене-
рального распределения и значение параметров распределения, которые и подлежат оценке.
Первое затруднение преодолевается тем, что иногда вид генерального распределения может постулироваться (нормальное распределение, равномерное распределение и т.д.). В некоторых случаях при достаточно большом объеме выборки реальную функцию распределения оценки с достаточной точностью можно заменить асимптотической (соответствующей n →∞). В частности, из
теоремы Ляпунова |
следует, что распределения выборочной |
средней |
|||||
|
|
|
= |
X1 + X 2 + ...+ X n |
или относительной частоты значения признака |
w = ni |
|
|
X |
B |
|||||
|
|
||||||
|
|
|
n |
|
i |
n |
|
|
|
|
|
|
|
||
распределены асимптотически нормально независимо от вида генерального распределения.
Попытки разрешения второго затруднения приводят к двум способам построения интервальной оценки: приближенному и точному.
Приближенный способ состоит в замене неизвестных параметров гене-
ральной совокупности, от которых зависит распределение Θ* , на их точечные оценки, полученные в результате выборки. Далее оценка строится, как если бы параметры распределения были бы известны.
Точный способ может быть использован лишь в том случае, когда известен закон генерального распределения. При этом строятся вспомогательные случайные величины, распределение которых не зависит от неизвестных параметров генеральной совокупности, но зависит лишь от объема выборки. В част-
5
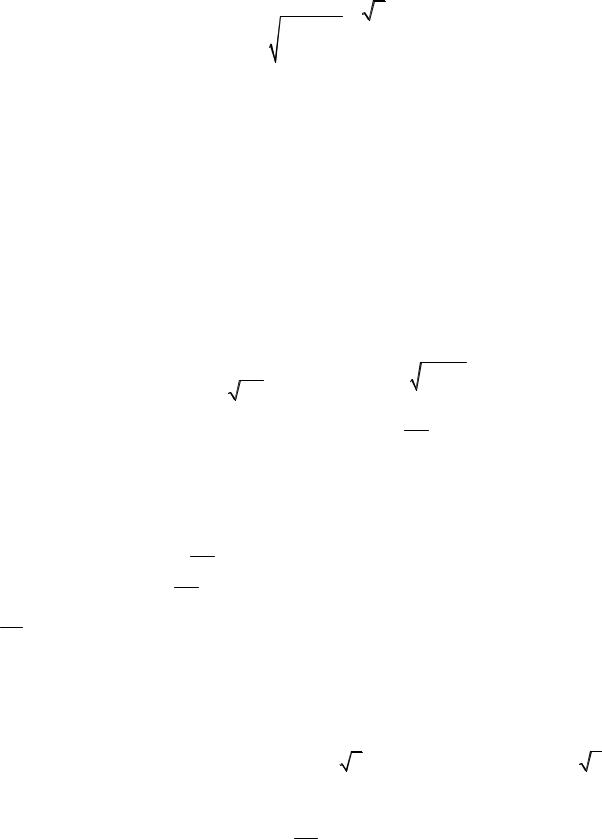
ности, при оценке среднего значения нормально распределенной генеральной совокупности можно использовать оценку
|
M [X ]− |
|
|
|
|||
* |
X B |
|
|
||||
Θ = T = |
|
|
|
|
|
|
n , |
|
n |
|
D |
|
|||
|
|
|
|
||||
|
|
n −1 |
|
|
|||
|
|
|
B |
|
|
||
которая подчиняется распределению Стьюдента, зависящему только от объема выборки n .
Синтервальной оценкой связано решение трех типов задач:
1)определение доверительной вероятности по заданному доверительному интервалу и объему выборки;
2)определение доверительного интервала по заданной доверительной вероятности и объему выборки;
3)определение необходимого объема выборки по заданным доверительной вероятности и доверительному интервалу.
Интервальная оценка математического ожидания нормально распределенной случайной величины
при известном σ.
Пусть случайная величина Х генеральной совокупности распределена по
|
|
|
1 |
e− |
( x−a )2 |
||||
нормальному закону |
f ( x ) = |
|
|
, где σ = D[Х], a = M [Х] = |
|
, |
|||
|
2σ2 |
||||||||
|
X |
||||||||
σ |
2π |
||||||||
|
|
|
|
|
|
|
|||
при этом среднее квадратическое отклонение σ считаем известным.
Пусть сделана выборка объема n и вычислена X B , которая является точечной оценкой математического ожидания a генеральной совокупности.
Так как |
|
= |
X1 + X 2 + ...+ X n |
– среднее арифметическое случайных величин |
|
X B |
|||||
n |
|||||
|
|
|
|
X1 ,X2 ,...,Xn , распределенных так же, как и признак генеральной совокупности X, то закон распределения X B также нормален, M [X B ]= M [X ]= a , а диспер-
сия случайной величины X B в n раз меньше дисперсии случайной величины X:
σ2 X B = σn2 .
1). Определим, с какой надежностью математическое ожидание а покрыва-
ется доверительным интервалом |
|
|
при |
заданной точности |
ε, т.е. |
найдем |
||||||||||||||||||||
P( |
|
|
−a |
|
<ε) или P ( |
|
−ε < a < |
|
|
|
+ε). |
|
|
|
|
|
|
|
|
|||||||
|
XB |
|
X B |
X B |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
ε n |
|
|
|
|
ε n |
|
||
Тогда, P ( |
Хв −a |
< ε)= 2Ф |
|
|
|
= 2Ф |
|
= 2Ф(t )= γ , |
где |
t = |
, |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
σ (Хв ) |
|
|
σ |
|
|
|
|
σ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где Ф(t) – функция Лапласа. Зная σ, ε и n, можно найти по таблице значений функции Лапласа надежность γ оценки X B математического ожидания a.
6

2). По выборочному значению математического ожидания X B и известному
σ найти доверительный интервал, который с заданной надежностью γ покрывает математическое ожидание а генеральной совокупности. Это и есть задача
получения интервальной оценки X B . Используя таблицы значений функции Лапласа, по γ определяют t = εσn , отсюда ε = tσn . Таким образом получают
искомый доверительный интервал, с надежностью γ покрывающий неизвест- |
||||||||
ный параметр а; точность оценки ε = |
tσ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
||
|
|
|
ε |
|
n |
|
|
|
3). По заданным σ, ε и γ, используя соотношение 2Ф |
|
σ |
=γ , найти объ- |
|||||
|
|
|
|
|
|
|
||
ем выборки n. Решая уравнение 2Ф(t)=γ , по γ находим t |
, а затем из t = |
ε n |
|
|||||
σ |
||||||||
|
|
|
|
|
|
|||
находим минимальный объем выборки n = tσ 2 .
ε
10.3.Интервальная оценка математического ожидания нормально распределенной случайной величины
при неизвестном σ.
Для решения этой задачи используется распределение Стьюдента случай-
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
Хв |
−a |
|
|
|
|
|
|
|
|
|
|
||||
ной величины |
t = |
, где sв = |
|
∑(xi − |
Х |
в )2 несмещенная оценка |
||||||||||||
s / |
n |
|
|
|||||||||||||||
|
|
|
|
n −1 i=1 |
|
|
|
|
|
|
|
|||||||
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
среднего квадратичного отклонения. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Плотность этого распределения : |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
−n |
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
t |
|
|
2 |
|||||
|
fn (t )= |
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
n −1 |
|
n −1 |
|
|
|||||||||||
|
|
|
|
|
|
|
π( n −1)Г |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fn ( t ) определяется только объемом выборки n и не зависит от неизвестных па-
раметров. При n→∞ распределение Стьюдента стремится к стандартному нормальному N (0,1), то практически при n > 30 можно пользоваться вместо рас-
пределения Стьюдента нормальным распределением.
Аналогично предыдущей задаче, по заданным n и γ находим в таблицах кван-
тиль распределения Стьюдента Учитывая, что t = Хв −a , можно записать sв / n
7
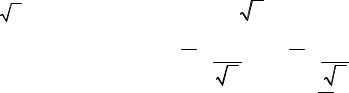
|
|
|
|
|
|
|
−a |
|
|
|
|
|
|
|
|
t |
s |
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|||||||||
P ( |
t |
< tγ )= P |
|
|
|
в |
|
|
< tγ |
|
=γ , или P |
|
Хв −a |
< |
γ |
в |
|
=γ , |
||
|
|
|
|
|
|
|
|
|
n |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
s / |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда доверительный интервал для a : Х − tγ snв < a < Х + tγ snв .
Итак, по имеющейся выборке x1 ,x2 ,...,xn находим Хв и sв . Затем, задава-
ясь надежностью γ, определяем доверительный интервал, покрывающий математическое ожидание а.
10.4. Интервальная оценка среднего квадратического отклонения σ нормального распределения
Пусть случайная величина Х распределена нормально и требуется оценить неизвестное генеральное среднее квадратическое отклонение (с.к.о.) σ по исправленному выборочному с.к.о. s . Точечной оценкой параметра σ служит исправленное выборочное с.к.о.. Построим доверительный интервал, покрывающий параметр σ с заданной надежностью γ .
Для решения этой задачи используется распределение χ2 (Пирсона). Для
выборки |
X |
|
,X |
|
,...,X |
|
величина |
s2 |
(n −1) |
= χ2 |
распределена по закону |
χ2 с n −1 |
1 |
2 |
n |
|
|
||||||||
|
σ2 |
|||||||||||
|
|
|
|
|
|
|
|
|
степенями свободы.
Рассмотрим симметричный доверительный интервал
P (s −δ <σ < s +δ )= γ .
Это приводит к оценке s (1−q)<σ < s (1+q), где числа q = q (n,γ ) ищутся по таблицам распределения χ2 .
Так как более доступны таблицы квантилей распределения χ2 , изложим еще один способ построения доверительного интервала, покрывающего гене-
ральное с.к.о. σ с заданной доверительной вероятностью. Запишем его в виде:
P (s −δ− <σ < s +δ+ )= γ ,
где границы s −δ− и s +δ+ пока не определены. Неравенства для σ могут быть
преобразованы в неравенства для χ2 = |
s2 (n −1) |
: P (χ2 |
− < χ2 < χ2 |
+ )=γ и вели- |
||||||||||
σ |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 −γ |
|
||
чины |
χ2 |
− и |
χ2 |
+ |
определяются |
из условий: |
P (χ2 ≤ χ2 |
− )= |
=α , |
|||||
|
||||||||||||||
P (χ2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
||
≥ χ2 |
+ )=α , |
P (χ2 |
≤ χ2 |
+ )=1 −α , т.е. являются квантилями распределения |
||||||||||
χ2 уровня α и уровня 1 −α , соответственно.
Часто в таблицах приводятся не квантили qp ( P (X < qp )= p ) , а критические точки распределений k p ( P (X > kp )= p ). Неравенства предыдущего раздела с
использованием критических точек будут выглядеть так:
P (χ2кр(−) < χ2 < χ2кр(+) )=γ ,
8
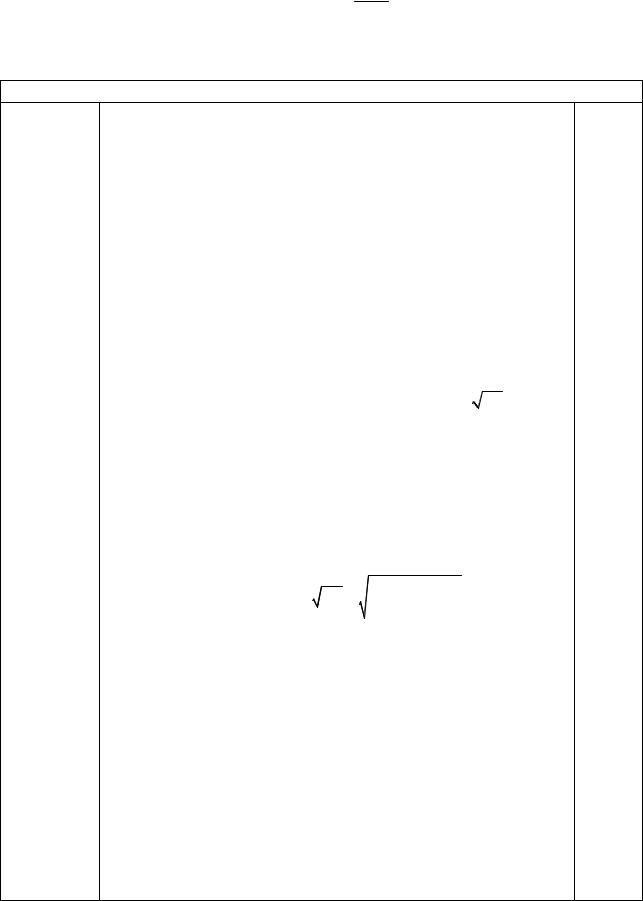
P (χ2 > χ2 кр(+) )= 1 −2γ =α ,
P(χ2 > χ2кр(−) )=1 −α .
ПП11.1. Точечные оценки параметров распределения
№ п/п |
Задание |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|||||||
|
Случайная величина X распределена по показательному |
||||||||||||||||||||
|
закону с плотностью распределения f (x)= λe−λx |
(x ≥ 0) |
и |
||||||||||||||||||
|
неизвестным параметром λ . Методом моментов по вы- |
||||||||||||||||||||
ПП |
борке x1 ,x2 ,...,xn оценить значение этого параметра. |
|
|
|
|||||||||||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
11.№1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M (X )= ∞∫xλe−λxdx = |
|
|
|
λx = t |
|
|
|
= |
1 |
∞∫te−t dt = |
1 |
= xB , т.е. λ = |
|
1 |
. |
|
|||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
λ 0 |
λ |
|
|
|
|
xB |
|
||||
|
Итак, оценка параметра распределения λ* = |
1 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
Случайная величина X |
распределена по нормальному |
|||||||||||||||||||
|
закону с плотностью распределения f (x)= |
|
1 |
|
e− |
(x−a)2 |
и |
||||||||||||||
|
|
|
2σ2 |
||||||||||||||||||
|
σ 2π |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
неизвестными параметрами a и σ . Методом моментов |
||||||||||||||||||||
|
по выборке x1 ,x2 ,...,xn оценить значение этих параметров. |
||||||||||||||||||||
ППРЕШЕНИЕ:
11.№2. Приравняем теоретические и эмпирические средние и |
||||||||||
дисперсии. Как известно, для нормального распределе- |
||||||||||
ния M (X )= a , D (X )=σ 2 . |
|
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
|
* |
x1 + x2 +...+ xn |
|
* |
|
1 n |
|
|
2 |
|
|
|
|
|
|
|||||||
a = xB = |
|
|
, σ |
|
= DB = |
∑(xi − xB ) |
|
. |
||
n |
|
|
|
|||||||
|
|
|
|
|
n i=1 |
|
|
|||
Случайная величина X распределена по биномиальному |
||||||||||
закону: |
|
Pm (X = xi )= Cmxi pxi (1− p)m−xi , |
|
|
||||||
|
|
|
|
|||||||
где m – длина серии испытаний, xi – число появлений |
||||||||||
события в i -й серии испытаний, n– объем выборки (чис- |
||||||||||
ППло проведенных серий испытаний), p – неизвестный па-
11.№3. раметр распределения (вероятность появления события в |
однократном испытании). Методом максимального прав- |
доподобия по выборке x1 ,x2 ,...,xn оценить значение этого |
параметра. |
РЕШЕНИЕ: |
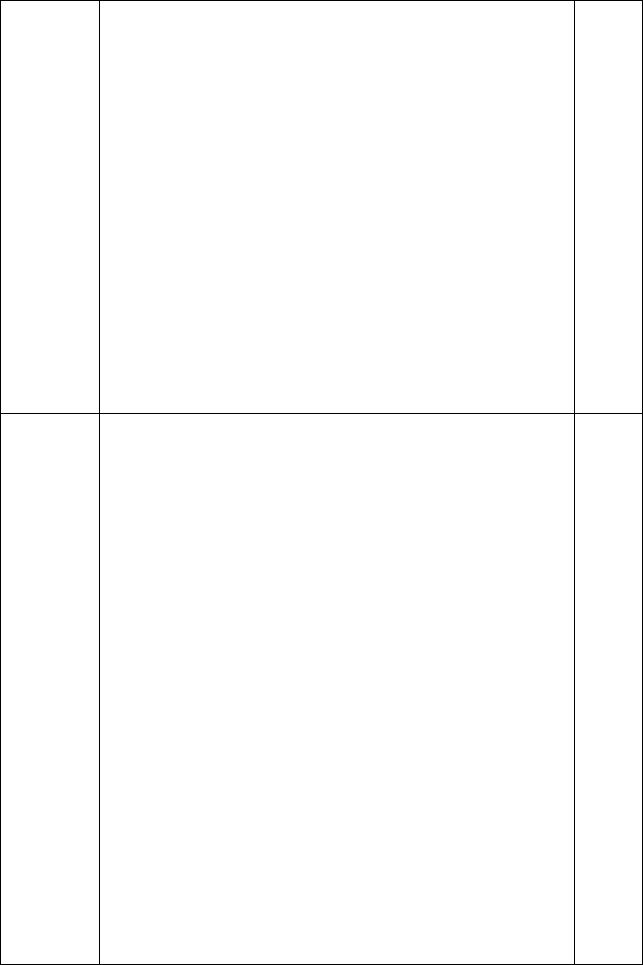
Составим функцию правдоподобия: |
9
|
|
|
x1 |
p |
x1 |
(1− p) |
m−x1 |
x2 |
p |
x2 |
(1− p) |
m−x2 |
|
|
|
|||||||
L (x1 ,x2 ,...,xn ; p)= Cm |
|
|
× |
Cm |
|
|
×... |
|
|
|||||||||||||
xn |
xn |
(1− p) |
m−xn |
|
|
x1 x2 |
|
xn |
) |
p |
x1 +x2 +...+xn |
(1− p) |
mn−(x1 +x2 |
+...+xn ) |
. |
|||||||
...× Cm p |
|
|
= (Cm Cm ... Cm |
|
|
|
|
|
|
|
|
|||||||||||
Логарифмическая функция распределения: |
|
|
|
|
|
|||||||||||||||||
ln L =ln(Cmx1 Cmx2 ... Cmxn |
)+(∑xi )ln p +(nm −∑xi )ln(1− p), |
|
|
|||||||||||||||||||
Уравнение правдоподобия: |
|
d ln L |
|
= |
∑xi |
− |
nm −∑xi |
= 0 , |
|
|
||||||||||||
|
dp |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
1− p |
|
|
|
|
|||
его решение (критическая точка): p = ∑nmxi . Проверим выполнение достаточных условий экстрему-
ма: |
|
d 2 ln L |
= − |
∑xi − |
nm −∑xi |
, при |
p = |
∑xi |
d 2 ln L |
< 0 , т.е., |
|
|
dp2 |
|
|
dp2 |
|||||||
|
|
|
|
p |
(1− p)2 |
|
nm |
|
|||
p = |
∑xi |
– точка максимума, и в качестве оценки макси- |
|||||||||
|
nm |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
мального правдоподобия параметра p биномиального распределения нужно взять p = ∑nmxi .
Случайная величина X распределена по закону Пуассона:
Pm (X = xi )= λxxi ei!−λ ,
где m – длина серии испытаний, xi – число появлений
события в i -й серии испытаний, n– объем выборки (число проведенных серий испытаний), λ – неизвестный параметр распределения. Методом максимального правдоподобия по выборке x1 ,x2 ,...,xn оценить значение этого
параметра. РЕШЕНИЕ:
ППСоставим логарифмическую функцию правдоподобия:
11.№4. |
ln L (x1 ,x2 ,...,xn |
|
|
|
λx1 e−λ |
|
λx2 e−λ |
|
λxn e−λ |
|
|
||||||||||
|
;λ)= ln |
x1! |
|
x2! |
|
|
... |
xn! |
= |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
λ∑xi |
|
|
|
|
|
|
) |
|
−nλ −ln (x ! x ! |
... x !). |
||||||||
|
= ln |
|
|
|
|
e−nλ = |
x |
|
ln λ |
||||||||||||
|
x ! x ! ... x ! |
|
|||||||||||||||||||
|
|
|
|
(∑ i |
|
|
|
|
|
1 |
2 |
n |
|||||||||
|
|
1 |
2 |
n |
|
|
|
|
|
|
|
|
|
|
(∑xi ) |
|
|
|
|||
|
Уравнение правдоподобия: d ln L |
= |
−n = 0 , его ре- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dλ |
|
λ |
|
|
|
|||||
|
шение (критическая точка): λ = |
(∑xi ) |
= |
|
. Проверим вы- |
||||||||||||||||
|
xB |
||||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
|
полнение достаточных условий экстремума: |
|
|||||||||||||||||||
|
d 2 ln L |
= − (∑xi ) |
< 0 , т.е., |
|
λ = |
|
– точка максимума, и в |
||||||||||||||
|
|
xB |
|||||||||||||||||||
|
dλ2 |
|
λ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10
