
Волны
.pdfВыведем уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Ox . Как известно, в плоскости фронта волны (в плоскости yOz и параллельных ей плоскостях) все частицы среды совершают колебания в одинаковой фазе, поэтому в уравнении волны будет отсутствовать зависимость от координат у и z: ξ(x,y,z,t)= ξ(x,t).
Для гармонической волны все частицы среды совершают колебания с одинаковой циклической частотой ω . Пусть в момент времени t = 0 частицы
среды с координатой x = 0, расположенные в плоскости |
yOz , начинают |
совершать колебания по закону |
|
ξ(0,t) = Acos(ωt +ϕ0 ) . |
(6.2) |
Частицы с координатой х начнут совершать ГК только после прихода к ним волны. Для этого требуется время τ = x / υ и поэтому уравнение колебаний для таких частиц примет вид:
ξ(x,t) = Acos(ω(t −τ)+ϕ0 ) = Acos(ωt − ωυ x +ϕ0 ) = Acos(ωt −kx +ϕ0 ). (6.3)
Уравнение (6.3) представляет собой уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Ox . В эту формулу входит волновое число к, которое связано с круговой частотой щ, фазовой скоростью υ волны и ее пространственным периодом λ соотношением
k = |
ω |
= |
2π . |
(6.4) |
|
υ |
|
λ |
|
Волновое число к представляет собой модуль волнового вектора k. Направление волнового вектора k совпадает с направлением скорости распространения бегущей волны, а его модуль определяется формулой (6.4).
Покажем, что входящая в формулу (6.3) фазовая скорость υ волны представляет собой скорость движения фиксированного значения фазы волны. Действительно,
ϕ = ωt −kx +ϕ0 = const, |
dϕ |
= ω−k dx |
= ω−kυ= 0 , |
|
dt |
dt |
|
х = |
щ |
, |
(6.5) |
что согласуется с формулой (6.4). |
k |
|
|
|
|
|
|
Волновым уравнением называют уравнение, решением |
которого |
||
является уравнение волны ξ(x,y,z,t). Найдем волновое уравнение для волновой
функции (6.3). Если взять частные производные по координате |
x и времени t |
|||||||
от ξ(x,y,z,t) |
|
|
|
|
|
|
|
|
∂ξ |
|
|
∂2ξ |
2 |
|
|
|
|
∂t |
= −Aωsin(ωt −kx +ϕ0 ) , |
∂t2 |
= −Aω cos(ωt −kx +ϕ0 ) , |
|
||||
∂ξ |
= Ak sin(ωt −kx +ϕ |
) , |
∂2ξ |
= Ak2 cos(ωt −kx +ϕ |
|
) , |
|
|
∂x |
0 |
|
∂x2 |
|
0 |
|
|
|
тогда волновое уравнение примет вид |
|
|
|
|||||
|
∂2 |
ξ = |
1 |
∂2ξ . |
|
|
(6.6) |
|
|
|
|
|
|
||||
|
∂x2 |
υ2 ∂t2 |
|
|
|
|||
51
Оказывается, что решением этого уравнения, кроме плоской гармонической волны, бегущей в положительном направлении оси Ox , является также плоская гармоническая волна, распространяющаяся в отрицательном направлении оси
Ox :
ξ(x,t) = Acos(ωt + kx +ϕ0 ) .
Для плоской гармонической волны, распространяющейся в произвольном направлении, которое можно задать радиус-вектором r , уравнение волны и волновое уравнение запишутся следующим образом
∂2ξ + |
∂2ξ |
+ |
∂2ξ |
= |
1 ∂2ξ |
, |
(6.7) |
||
|
|
|
|
||||||
∂y2 |
∂t2 |
υ2 ∂t2 |
|||||||
∂x2 |
|
|
|
|
|||||
ξ(r ,t) = Acos(ωt −kr +ϕ0 ). |
(6.8) |
||||||||
Можно показать, что волновому уравнению (6.7) удовлетворяет также и уравнение сферической волны
ξ(r ,t) = A(r)cos(ωt −kr +ϕ0 ) |
(6.9) |
Это уравнение отличается от уравнения плоской гармонической волны тем, что для сферической волны амплитуда А будет зависеть от расстояния r между точечным источником колебаний и рассматриваемой точкой пространства, а именно, амплитуда сферической волны убывает обратно пропорционально расстоянию r.
Действительно, амплитуда колебаний частиц среды определяется энергией W волны, приходящейся на единицу поверхности фронта волны (площадь поверхности фронта волны равна S = 4πr2 ) вблизи рассматриваемой точки, и поэтому
А ~ |
W |
~ |
W |
~ |
1 |
. |
S |
4πr2 |
|
||||
|
|
|
r |
|||
В заключение этого параграфа рассмотрим ряд примеров, поясняющих распространение плоской гармонической волны (6.3) в положительном направлении оси Ox .
Пример 1. Записать уравнение колебаний для смещения ξ частицы среды с
координатой x , равной λ ( x = λ), около своего положения равновесия в зависимости от времени t (начальную фазу колебаний источника взять равной нулю: ϕ0 = 0 ). Построить график этой зависимости в пределах одного периода.
Подставляя в формулу (6.3) значение x = λ, получим
ξ(λ,t) = Acos(ωt −kx +ϕ0 ) = Acos(ωt −2π) = Acos(ωt) = Acos(2Tπt) ,
график этой зависимости представлен на рис. 6.5,а.
52
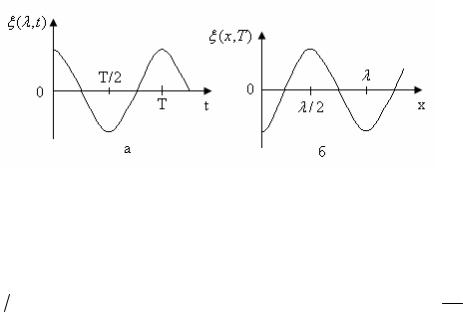
Рис. 6.5
Пример 2. Записать уравнение, описывающее положения всех частиц среды около своих положений равновесия в момент времени t=Т/2 при начальной фазе колебаний источника ϕ0 = 0 . Построить график этой зависимости.
Подставляя в формулу (6.3) значение t = T / 2 , получим
ξ(х,Т 2) = Acos(ωt −kx +ϕ0 ) = Acos(π−кх) = −Acos(кх) = −Acos(2λπх) ,
график этой зависимости представлен на рис. 6.5,б. Из него следует, что периодом по координате является длина волны λ, т.е. через расстояние вдоль скорости распространения волны, равное длине волны λ, повторяются смещения частиц относительно своих положений равновесия.
Пример 3. Найти разность фаз ∆ϕ колебаний двух частиц среды, отстоящих от источника колебаний на расстоянии x1 и x2 соответственно.
Согласно уравнению (6.3), запишем
∆ϕ =ϕ2 −ϕ1 = (ωt −kx2 +ϕ0 )−(ωt − kx1 +ϕ0 ) = −k(x2 − x1) = − 2λπ∆x .
Пример 4. Рассчитать отношение максимальной скорости υm колебаний
частиц воздуха к скорости υ звуковой волны (υ =330 м/с), если амплитуда А колебаний частиц среды равна А=0,2 мм.
Используя для максимальной скорости υm колебаний формулу (5.9), получим
υ |
= |
Aω |
= |
A2πν |
= |
2 3,14 2 10−4 |
(16 −20 000)= (0,61 10 |
−4 |
−0,076) , |
|
υ |
υ |
υ |
330 |
|
||||||
m |
|
|
|
|
|
|
|
|
|
|
т.е. для волн звуковой частоты скорость распространения колебаний в воздухе значительно превосходит максимальную скорость колебаний частиц воздуха.
6.1.3.Энергия упругой волны. Объемная плотность энергии. Вектор Умова
Упругая волна, распространяясь в среде, несет с собой энергию от источника колебаний, что приводит к появлению в среде дополнительной энергии, связанной с колебаниями частиц среды – это и есть энергия волны. Запишем для нее формулу. Для этого рассмотрим плоскую продольную гармоническую волну (6.3), распространяющуюся в положительном направлении оси Ox .
53
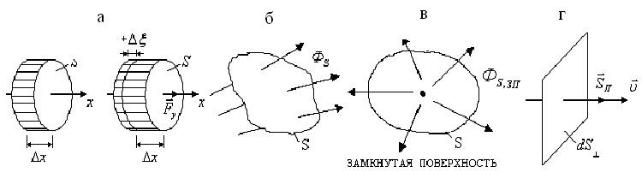
Для малого объема среды (он представляет собой цилиндр площади основания S и высоты ∆x, рис. 6.6,а) скорости всех частиц будут одинаковы
νX = ∂∂ξt = −Aωsin(ωt − kx +ϕ0 ) ,
ипоэтому кинетическая энергия частиц в этом объеме, связанная с их колебаниями около своих положений равновесия, будет равна
W |
= |
mν2 |
= |
1 |
2 |
2 2 |
(ωt −kx +ϕ |
), |
W |
= |
1 |
2 |
2 |
|
|
ρVA |
ω sin |
|
ρVA |
ω , (6.10) |
|||||||
K |
2 |
|
2 |
|
|
0 |
|
Km |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
где введена плотность с среды, позволяющая выразить массу m всех частиц в объеме V.
Величина деформации этого малого объема будет равна До, а относительная деформация (∆ξ/∆x) в виду малости объемаV (V = S∆x ) (см. рис. 6.6,а) будет равна (∆ξ/∆x) = (∂ξ/∂x) . Потенциальную энергию WР такого деформированного
объема можно оценить по формуле: WР = 12 kЖ (∆ξ)2 , где kЖ представляет коэффициент жесткости среды.
Рис. 6.6
Обычно упругие свойства твердого тела определяют модулем Е Юнга, который характеризует сопротивляемость материала упругой твердой среды деформациям сжатия или растяжения. Поэтому выразим потенциальную энергию через модуль Е Юнга. Для этого на основе двух выражений закона Гука запишем формулу связи между коэффициентом kЖ жесткости и модулем Юнга:
σ= Eε, |
F |
= k |
Ж |
∆ξ, |
σ= |
FУ |
, |
ε = ∆ξ, k |
Ж |
= ES / ∆x , |
(6.11) |
|
|||||||||||
|
У |
|
|
|
S |
∆x |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
где величина у называется механическим напряжением, а ε–относительным удлинением.
Тогда для потенциальной энергии WР деформированного объема можно записать
W |
= |
1 k |
|
(∆ξ)2 |
= |
1 |
(ES /∆x) (∆ξ2 ) = |
1 E(S∆x) ( |
∆ξ)2 = |
1VE( |
∂ξ)2 |
|
||||
Р |
|
2 |
Ж |
|
|
2 |
|
|
2 |
|
|
∆x |
|
2 |
∂x |
|
W |
= |
1 VE(∂ξ)2 |
=W |
sin2 (ωt −kx +ϕ |
), |
W |
|
= 1VEk2 A2 . |
(6.12) |
|||||||
Р |
|
2 |
|
∂x |
|
|
P max |
|
0 |
|
P max |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
54
В случае жидких и газообразных сред вместо модуля Е Юнга нужно в формулу (6.12) подставить модуль k объемной упругости газа или жидкости, который характеризует способность газа или жидкости сопротивляться изменению их объема.
Из теории колебаний известно, что максимальные значения кинетической и потенциальной энергий при ГК совпадают:WKm =WPm , и поэтому
W |
= |
1 ρVA2ω2 sin2 (ωt −kx +ϕ |
) . |
(6.13) |
|
Р |
|
2 |
0 |
|
|
|
|
|
|
|
|
Следовательно, полную энергию волны в объеме V можно представить в следующем виде:
W =W |
K |
+W |
P |
= ρVA2ω2 sin2(ωt −kx +ϕ |
0 |
). |
(6.14) |
|
|
|
|
|
|
||||
Эта формула позволяет ввести объемную плотность энергии w волны |
|
|||||||
w = dW |
= W |
= ρA2ω2 sin2 (ωt −kx +ϕ0 ), |
|
|
(6.15) |
|||
dV |
|
|
V |
|
|
|
|
|
где учтено, что рассматриваемый объем V является малым.
Из формулы (6.15) следует, что объемная плотность энергии бегущей волны зависит от координат и времени по гармоническому закону, т.е. представляет собой бегущую волну энергии колебаний в среде,
следовательно, в среде происходит перенос энергии источника колебаний. Полученные выражения справедливы и для поперечной волны, которая распространяется только в твердых телах. В этом случае вместо модуля Юнга необходимо записывать в формулах модуль сдвига G.
Введем энергетические характеристики, описывающие перенос энергии волнового процесса в среде.
1. Мощность излучения источника колебаний PИ – это энергия,
излучаемая источником колебаний за единицу времени |
|
||
PИ = |
dW |
. |
(6.16) |
|
|||
|
dt |
|
|
2. Поток энергии ФS через какую-либо поверхность S |
– это энергия, |
||
переносимая через какую-либо поверхность за единицу времени (рис. 6.6,б)
ФS = |
dWS |
. |
(6.17) |
|
|||
|
dt |
|
|
Из формулы (6.17) следует, что мощность излучения источника равна потоку энергии ФS ,ЗП через замкнутую поверхность, окружающую источник
колебаний: PИ =ФS ,ЗП (рис. 6.6, в).
3.Вектор Умова или вектор плотности потока энергии SП – это вектор,
направление которого совпадает с направлением скорости волны, а его модуль равен энергии, переносимой за единицу времени, через единичную площадку dS , расположенную перпендикулярно направлению переноса энергии
(рис.6.6,г):
SП = |
dW |
. |
(6.18) |
|
|||
|
dS dt |
|
|
55
Для модуля вектора Умова можно получить следующую формулу
SП = |
dW |
= |
dW |
|
υ |
= |
dWυ |
= dW |
υ= wυ , |
|
dS dt |
dS dt |
υ |
dS dl |
|||||||
|
|
|
|
dV |
|
где введена объемная плотность энергии волны в среде. Тогда для вектора Умова можно записать
SП = wυ= ρA2ω2sin2 (ωt −kx +ϕ0 )υ. |
(6.19) |
4. Интенсивность упругой волны I равна усредненному по времени значению модуля вектора Умова
I = SП |
= w х= |
1 |
сA2щ2х. |
(6.20) |
|
|
2 |
|
|
Введение интенсивности I связано с тем, что многие приборы при достаточно высокой циклической частоте щ волны измеряют не мгновенное, а усредненное по времени значение модуля вектора Умова.
6.1.4. Стоячие волны. Колебания струны
Стоячей волной называют волну, образующуюся при сложении двух встречных волн одинаковой частоты и амплитуды
ξ1(x,t) = Acos(ωt − kx) , ξ2 (x,t) = Acos(ωt + kx) .
Для простоты здесь рассмотрен случай сложения двух плоских волн, распространяющихся вдоль оси Ох в положительном ( ξ1(x,t) ) и отрицательном ( ξ2 (x,t) ) ее направлениях. Для уравнения стоячей волны в соответствии с формулой сложения косинусов можно записать
ξСТ (x,t) = ξ1 + ξ2 = 2Acoskxcosωt . |
(6.21) |
||||
Из формулы (6.21) следует, что амплитуда стоячей волны |
(6.22) |
||||
AСТ = |
|
2Acoskx |
|
|
|
|
|
||||
зависит от координаты x выбранной точки пространства, |
изменяясь от |
||||
минимального значения, равного нулю, до максимального значения, равного
2А.
Найдем координаты точек пространства ( x = xП ), в которых наблюдается максимальная амплитуда колебаний частиц среды, их называют пучностями стоячей волны, и координаты узлов стоячей волны ( x = xУ ), для них амплитуда колебаний частиц среды равна нулю
х = х |
|
: |
А = 2А |
cos kx = ±1 |
2π |
х |
|
= πn |
|
λ |
|
||||||
|
п |
|
СТ |
п |
|
п |
|
|
|
|
|
x |
= лn |
, |
|
|
n = 0,1,2,.., |
|
|
|
|
|
(6.23) |
|
|
|
|
|
п |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2р |
|
|
|
р |
|
|
х = х |
|
: |
А = 0 |
|
|
cos kx |
|
|
= 0 |
х |
|
= |
+ рn |
|||
|
|
|
|
λ |
|
2 |
||||||||||
|
уз |
|
СТ |
|
λ |
|
|
уз |
|
|
уз |
|
|
|||
|
|
|
|
xуз = |
(n + |
1 |
) |
, n = 0,1,2... |
|
|
|
|
(6.24) |
|||
|
|
|
|
2 |
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
56

Из формул (6.23) и (6.24) следует, что расстояние между соседними узлами ∆хУ и соседними пучностями ∆хП стоячей волны одинаково и равно
∆х = ∆хП = ∆хУ = λ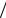 2.
2.
На рис. 6.7 приведены фотографии стоячей волны для трех моментов времени t=0,Т/4 ,Т/2. На них стрелками указаны направления движения частиц среды. Из графиков видно, что все частицы среды, находящиеся между соседними узлами, совершают колебания с разными амплитудами и с одинаковой фазой (частицы одновременно достигают положения равновесия и движутся в одну сторону). При переходе через узел фаза колебаний частиц изменяется на р (частицы по разные стороны от узла одновременно достигают положения равновесия и движутся в противоположных направлениях).
Как следует из графиков, приведенных на рис. 6.7, при образовании в среде стоячей волны в среде не происходит переноса энергии от источника
Рис. 6.7
колебаний, так как положение узлов и пучностей с течением времени не изменяется; перенос энергии встречных волн одинаковый и происходит в противоположных направлениях.
Наблюдается переход потенциальной энергии колебаний, сосредоточенной в основном в узлах см. (рис. 6.7, момент времени t = 0 ), в кинетическую энергию
57
колебаний, сосредоточенную в основном в пучностях стоячей волны см. (рис. 6.7, момент времени t = T / 4 ) и наоборот. Средний же по времени поток энергии в любом сечении стоячей волны равен нулю.
Действительно в соответствии с формулами (6.10), (6.12) и (6.21) для кинетической и потенциальной энергий частиц в случае стоячей волны можно записать следующие формулы
WР = 12VE(∂∂ξx )2 = 2WP max sin2 kx cos2 (ωt −kx +ϕ0 ) ,
W = |
mν2 |
= m ( |
∂ξ)2 = 2W |
cos2 kxsin2 (ωt −kx +ϕ |
) , |
|
|
||||||
K |
2 |
2 |
∂t |
K max |
0 |
|
|
|
|
|
|||
из которых видно, что наибольшая потенциальная энергия частиц наблюдается в узлах стоячей волны (sin2 kx =1 x = xУЗ ), а наибольшая кинетическая энергия частиц будет в пучностях стоячей волны
( cos2 kx =1 x = xП ).
Стоячие волны обычно образуются при отражении бегущей волны от границы раздела двух сред. При этом возможны два случая. В первом случае при отражении волны от более плотной среды фаза волны изменяется на значение, равное р, и на границе раздела ( x = xГР ) образуется узел стоячей
волны
ξПАД хГР,t)+ξОТР(xГР,t) = Acos(ωt −kxГР)+ Acos(ωt −kxГР + π) = 2Acosπ2 cos(ωt −kxГР + π2) = 0.
Во втором случае при отражении волны от менее плотной среды фаза волны не изменяется, и на границе раздела ( x = xГР ) образуется пучность стоячей
волны
ξПАД хГР,t)+ξОТР (xГР,t) = Acos(ωt −kxГР )+ Acos(ωt − kxГР ) = 2Acos(ωt − kxГР )
Если, например, в деревянной линейке, закрепленной на одном конце, возбудить стоячую волну, то на втором свободном конце будет либо пучность (отражение бегущей по линейке волны от границы раздела дерево – воздух, рис. 6.8,а), либо узел стоячей волны (отражение бегущей по линейке волны от границы раздела «дерево-вода», рис. 6.8,б). Причем на длине линейки укладывается половина длины волны.
Наиболее наглядным примером стоячей волны являются колебания струны, закрепленной на концах. Возбуждение в ней поперечных колебаний приводит к образованию стоячей волны, узлы которой приходятся на закрепленные концы
58
Рис. 6.8 (см. § 5.13, рис. 5.27,в и рис. 6.8,в). На длине струны укладывается целое
число полуволн, что позволяет найти частоты нормальных колебаний струны
( § 5.13, формула (5.92)):
= n |
л |
, λ |
= |
2 |
н |
= |
х |
= |
х |
n = нn , n=1,2,3,… |
2 |
|
|
2 |
|||||||
|
n |
|
n |
n |
|
лn |
1 |
|||
Любое произвольное колебание струны можно представить в виде суммы ее нормальных колебаний.
6.1.5. Интерференция волн
Рассмотренные в предыдущем параграфе стоячие волны являются частным случаем интерференции волн. Под интерференцией волн понимают такое
сложение в пространстве двух (или нескольких) волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны. Интерферировать могут только
когерентные волны, для них разность фаз не зависит от времени. |
|
|||||||||
Пусть два точечных источника S1 и S2 |
излучают когерентные волны, которые |
|||||||||
пройдя расстояния r1 и r2 складываются в точке В (рис. 6.9) |
|
|||||||||
ξ1 = A1cos(ω1t −k1x1 +ϕ01) , |
|
|
ξ2 = A2 cos(ω2t −k2x2 +ϕ02 ) |
|
||||||
Как видно из разности фаз складываемых колебаний |
|
|||||||||
∆ϕ =ϕ2 −ϕ1 = (ω2t −k2 r2 +ϕ02 )−(ω1t −k1r1 +ϕ01) = |
|
|||||||||
= (ω −ω)t −(k r |
−k r )+(ϕ |
02 |
−ϕ |
01 |
) = const , |
(6.25) |
||||
2 |
1 |
2 |
2 |
1 1 |
|
|
|
|
||
когерентные волны – это прежде |
всего волны одинаковой |
частоты: |
||||||||
ω1 = ω2 . |
наблюдается сложение колебаний одного направления и |
|||||||||
Пусть в точке B |
||||||||||
одинаковой частоты. Используя результаты § 5.7.1, можно записать формулу для квадрата амплитуды суммарного колебания в точке B :
A2 = A12 + A22 + 2A1 A2 cos ∆ϕ.
Учитывая равенство частот складываемых колебаний ( ω1 = ω2 ), для разности фаз ∆ϕ можно записать
59

∆ϕ = − |
2π∆ +(ϕ |
02 |
−ϕ |
01 |
), |
∆ = (r −r ) , |
|
|
λ |
|
|
2 |
1 |
||
|
|
|
|
|
|
|
|
где величина ∆ обозначает геометрическую разность хода волн в точке В. Запишем условия максимального усиления и ослабления амплитуды суммарной волны при интерференции для случая, когда начальные фазы колебаний будут одинаковы: ϕ01 = ϕ02 .
Рис. 6.9
1. Условие интерференционных максимумов
∆ϕ = − |
2π∆ = ±2πm, |
∆ = ± |
λ |
2m, m = 0,1,2,... A = A1 + A2 , (6.26) |
|
λ |
|
2 |
|
т.е. разность фаз колебаний равна четному числу π или на геометрической разности хода укладывается четное число полуволн.
2. Условие интерференционных минимумов
∆ϕ = − |
2π∆ = ±π(2m +1), ∆ = ± |
λ |
(2m +1), |
m = 0,1,2,... |
A = |
|
А1 − А2 |
|
, (6.27) |
|
|
|
|||||||||
|
λ |
|
2 |
|
|
|
|
|
|
|
т.е., разность фаз |
колебаний равна |
нечетному |
числу р |
|
или на |
|||||
геометрической разности хода укладывается нечетное число полуволн. Входящее в эти формулы число m называют порядком
интерференционного максимума или интерференционного минимума.
Если частота складываемых волн будет большой (т.е. период колебаний будет малым по сравнению со временем наблюдения или временем измерения приборов), то тогда необходимо провести усреднение формулы для амплитуды суммарного колебания по времени наблюдения, т.е. перейти к интенсивности волн ( I ~ A2 ):
|
I = I1 + I2 + 2 I1I2 cos∆ϕ . |
(6.28) |
|
Для |
некогерентных волн |
разность фаз ∆ϕ будет |
зависеть от времени, |
поэтому |
cos ∆ϕ усредняется |
до нуля ( cos ∆ϕ = 0 ) |
и интерференции не |
наблюдается, т.е. отсутствует устойчивая во времени картина усиления и ослабления амплитуды результирующей волны в разных точках пространства.
6.1.6. Волновой пакет. Групповая скорость. Дисперсия волн
Гармоническая (синусоидальная) волна с частотой ω является идеализацией, т.е. в реальных случаях ее не существует. Это связано с тем, что для нее разброс по частотам ∆ω равен нулю ( ∆ω= 0). Поэтому, в соответствии с формулой (5.43), время излучения такой волны стремится к бесконечности ( ∆τ ≈ 2π/∆ω= ∞ ). Это означает, что такая синусоидальная волна занимает все пространство ( ∆x = υ ∆τ = ∞ ) и никакой полезной информации в себе не несет.
В реальных случаях время излучения ф волны частоты ω является конечным, т.е. волна занимает ограниченную область пространства ( ∆x = υ ∆τ < ∞) и имеет
60
