
Волны
.pdf
5.10.2. Резонансные кривые для амплитуды напряжения на конденсаторе, для амплитуды смещения в механической системе. Явление резонанса
Исследуем функциюUCm (ω) (5.67) для различных значений угловой частоты внешнего напряжения ω .
1. |
ω=0: U |
Cm |
(0)= |
Um |
= |
ω2 |
= |
1 |
|
=U |
m |
, |
|
LCω2 |
LC |
||||||||||||
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. постоянное напряжение, подаваемое в контур, представляет собой напряжение на конденсаторе или все резонансные кривые для частоты ω , равной нулю ( ω= 0), выходят из одной точки.
2. ω → ∞: |
UCm → |
Um |
→ 0 , |
2 |
|||
|
|
LCω |
|
т.е. при больших частотах внешнего воздействия все резонансные кривые стремятся к нулю. Это связано с тем, что система не успевает за изменениями внешнего воздействия и амплитуда колебаний в контуре уменьшается.
3. ω = ωР . Найдем угловую частоту ωP , при которой зависимость
имеет максимальное значение. Оно будет наблюдаться в том случае, когда выражение под знаком квадратного корня в формуле (5.67) будет минимальным. Поэтому
2 |
2 |
) |
2 |
+ |
2 |
2 |
′ |
= 0 |
|
((ω0 |
− ω |
|
4β |
ω ) |
|||||
ωP = |
ω0 |
2 − 2β2 . |
|
|
(5.69) |
||||
Подставляя ωP в формулу (5.67), для максимального значения амплитуды напряжения на конденсаторе получим
UCm (ωp )= |
Um |
. |
(5.70) |
|
|||
|
LCβω |
|
|
|
3 |
|
|
Величина ωР получила название резонансной частоты. В условиях малого затухания (Q >>1) для частоты ω = ωР можно записать
2
UCm (ωp )=UmQ ωω0 =UmQ, UCm (ωp ) Um , (5.71)
3
т.е. амплитуда вынужденных колебаний напряжения на конденсаторе во много раз превышает амплитуду внешнего напряжения, подаваемого в контур. Это явление получило название явления резонанса. Под резонансом понимают
явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к частоте собственных свободных незатухающих колебаний системы.
На рис. 5.17,а |
приведены резонансные кривыеU |
Cm ( |
ω для идеального |
|
|
) |
|
колебательного контура ( R = 0, β = 0 ) и для двух значений сопротивления R в |
|||
нем ( R2 > R1 , т.е. β2 |
>β1 ). При этом считается, что индуктивность L катушки и |
||
электроемкость C конденсатора контура не изменяются, т.е. частота ω0 при этом остается неизменной.
31
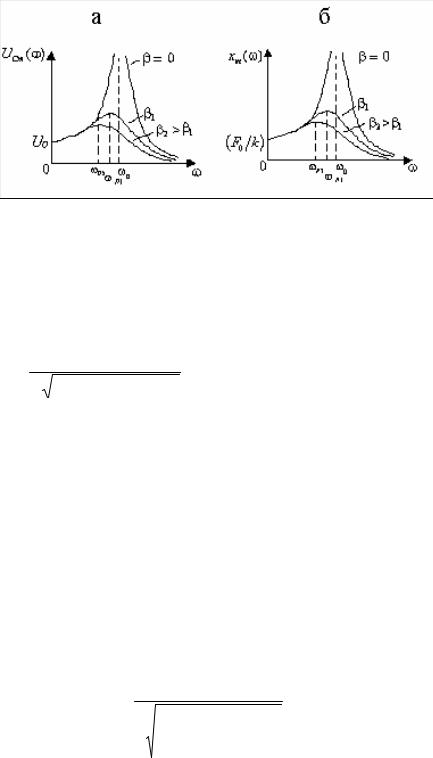
Можно отметить, что для идеального колебательного контура максимум
резонансной кривой U |
ω приходится на частоту ω , равную ω |
( ω= ω ), |
|
|
Cm ( ) |
0 |
0 |
причем максимальное |
значение |
при этом стремится к бесконечности |
|
(рис.5.17,а). При увеличении сопротивления R контура коэффициент затухания β увеличивается, а максимальное значениеUCm (ωp ) и частота ωР , на которую
он приходится, уменьшаются (рис. 5.17,а).
Рис. 5.17
В случае механической системы резонансную кривую хm (ω) для амплитуды
смещения груза (м.т.) от положения равновесия можно получить, используя табл. аналогий 5.1:
Uвнеш |
=U m cosωt → |
Fвнеш х = Fm cosωt ; |
|
|
|
|
|||||
qm (ω) → xm (ω) = |
Fm |
; xm (0) = |
|
Fm |
; |
xm (ω → ∞) → 0 . |
|
|
(5.72) |
||
m (ω02 −ω2 )2 + 4β2ω2 |
|
|
|
|
|||||||
|
|
|
k |
|
|
|
|
|
|
||
|
qm (ωp )= CUCm (ωp )= |
|
Um |
|
→ xm (ωp )= |
Fm |
|
. |
(5.73) |
||
|
2Lβω |
|
2mβω |
||||||||
|
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
3 |
|
|
|||
Графики резонансных зависимостей хm от ω при различных значениях коэффициента затухания β , т.е. при различных значениях коэффициента r сопротивления среды, и постоянной частоте ω0 приведены на рис .5.17,б.
5.10.3. Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе
Запишем формулу (5.68) для амплитуды силы тока Im (ω) в наиболее удобном виде
Im (ω) = |
|
|
Um |
|
, |
|
|
ω 2 |
−ω2 |
2 |
|||
|
|
|||||
L |
|
0 |
|
|
+ 4β2 |
|
|
ω |
|||||
|
|
|
|
|
||
|
|
|
|
|
|
и исследуем эту зависимость для различных значений ω.
1. ω=0 : Im (0) = 0 , т.е. постоянный электрический ток через цепь, содержащую конденсатор, не протекает.
32
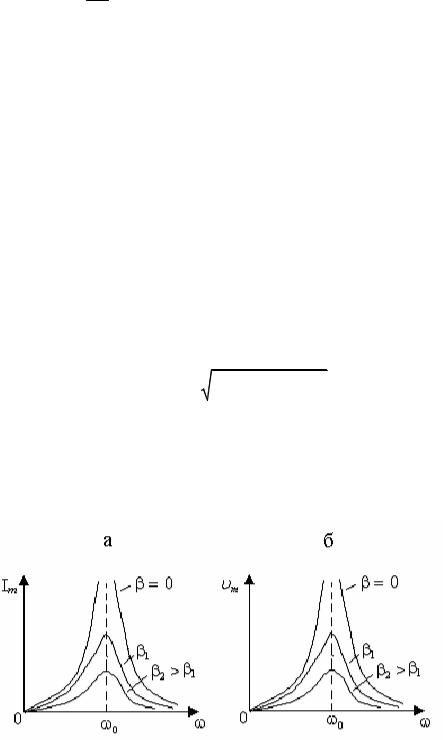
2.ω→ ∞: Im (ω → ∞) → ULωm → 0 .
3.Максимум функцииIm (ω) наблюдается тогда, когда подкоренное выражение в
знаменателе будет минимальным, т.е. первое слагаемое в подкоренном выражении должно быть равным нулю. Поэтому максимум Im (ω) соответствует
частоте ωP = ω0 , а само максимальное значение будет равно |
|
||
Im (ω0 ) = |
Um |
. |
(5.74) |
|
|||
|
R |
|
|
На рис. 5.18 приведены резонансные кривые Im (ω) в случае идеального колебательного контура ( R = 0, β = 0 ) и для двух разных значений сопротивления R в нем ( R2 > R1 , т.е. β2 > β1 ) при постоянном значении ω0 . Как видно,
максимум функции с увеличением R уменьшается, а его смещение по оси частот ω не происходит.
Используя табл. аналогий 5.1, можно записать формулы, описывающие
резонансные кривые для амплитуды колебаний скорости υ |
ω тела (м.т.) в |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ( |
) |
механической системе: |
|
|
|
|
|
|
Fmω |
|
|
|
||||||
|
|
|
|
I |
|
ω |
→ υ |
ω |
|
= |
|
|
, |
(5.75) |
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
m ( |
) |
m ( |
|
) |
|
|
m (ω02 −ω2 )2 +4βω2 |
|
|||
|
|
|
|
|
|
|
ωp = ω0 |
: |
|
υm (щ0 )= |
Fm |
. |
(5.76) |
|||
|
|
m ( |
|
|
|
|
|
r |
||||||||
График |
υ |
ω |
для |
трех |
|
|
значений |
коэффициента |
сопротивления |
|||||||
|
|
|
||||||||||||||
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( r = 0 , r2 |
> r1 ≠ 0) ) |
среды приведены на рис. |
5. |
18,б. Эти графики аналогичны |
||||||||||||
графикам резонансных кривых Im (ω) . |
|
|
|
|
||||||||||||
Рис. 5.18
33
5.10.4. Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые
Перепишем формулы (5.64) для I и UC в удобном виде
|
|
′ |
|
|
π |
|
q |
|
|
|
|
|
I = q |
= −Im sin(ωt − ψ) = Im cos(ωt − ψ + 2 ) , |
UC = C =UCm cos(ωt −ψ) , |
|
|
|
|||||||
|
|
|
|
|||||||||
и добавим к ним формулы для UL и UR: |
|
|
|
|
π |
|
||||||
|
dI |
|
|
π |
|
|
|
|
|
|
||
UL = L |
|
|
= −ULm sin(ωt − ψ + |
|
) = ULm cos(ωt −ψ + π) ,UR = IR =URm cos |
ωt −ψ+ |
2 |
|
.(5.77) |
|||
dt |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Найдем в соответствии с полученными формулами разность фаз колебаний между силой тока ϕI и напряжениями на конденсаторе ϕC , индуктивности ϕL и
активного сопротивления ϕR :
|
ωt −ψ+ |
π |
= − |
π |
, |
(5.78) |
|
∆ϕC,I = (ϕC −ϕI )= (ωt −ψ)− |
2 |
|
2 |
||||
|
|
|
|
|
|
||
∆ϕL,I |
= (ϕL |
|
ωt −ψ+ |
π |
= |
π |
, |
(5.79) |
|
−ϕI )= (ωt −ψ+ π)− |
2 |
|
2 |
||||||
|
|
|
|
|
|
|
|
||
∆ϕR,I = (ϕR −ϕI )= (ωt −ψ)−(ωt −ψ)= 0 . |
|
|
|
|
(5.80) |
||||
Как следует из формул
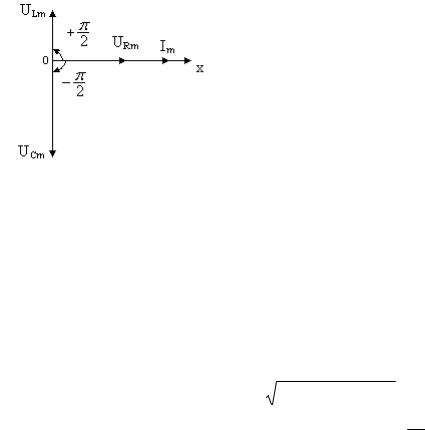
Рис. 5.19
электрической цепи. При принимается равной нулю, вдоль оси Ox .
На такой диаграмме
(5.78) – (5.80) фаза колебаний напряжения на
конденсаторе отстает по фазе от колебаний тока в цепи на π/2, а фаза колебаний
напряжения на катушке опережает фазу колебаний силы тока на π/2. Фазы колебаний
напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.
На ней указаны амплитуды векторов
напряжений |
на |
отдельных |
участках |
этом фаза колебания |
силы тока в |
контуре |
|
т.е. амплитуда вектора силы тока располагается вектор амплитуды внешнего напряженияUm ,
подаваемого в колебательный контур, можно представить как сумму векторов амплитуд напряжений (UC ,UL ,UR ) на разных его участках. Это позволяет
записать следующую формулу для модуля вектора амплитуды внешнего напряжения (например, для частот ω < ω0 , рис. 5.20,а):
Um = (UCm −ULm )2 +UR2 , |
(5.81) |
из которой с учетом формул (5.19) и (5.20) (UCm = qCm , ULm = Lω2qm , URm = ωRqm )
можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения
34
|
q |
2 |
2 |
|
(ω02 −ω2 ) |
2 |
|
||
Um = |
|
m |
− Lω2qm |
+(ωRqm ) |
|
= qm L |
|
+4β2ω2 |
|
C |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
qm = |
|
Um |
. |
|
L |
(ω02 −ω2 )2 +4β2ω2 |
|||
|
|
Рис. 5.20
Под фазовыми резонансными кривыми понимают, например, зависимости разности фаз ∆ϕВНЕШ, C между внешним напряжением UВНЕШ и напряжением UC
на конденсаторе, разности фаз ∆ϕВНЕШ, I между внешним напряжением UВНЕШ и
силой тока I в контуре от частоты щ внешнего напряжения. Наиболее интересными из них являются зависимости ∆ϕВНЕШ, I (щ), так как они позволяют выяснить эффективность поступления энергии в контур (колебательную систему). В соответствии с формулами (5.64) и (5.66) для разности фаз ∆ϕВНЕШ, C
и ∆ϕВНЕШ, |
I можно записать |
|
|
|
|
|
|
|
|
|
||||
∆ϕВНЕШ, C |
= ωt −(ωt −ψ)= ψ , ∆ϕВНЕШ, I = ωt |
|
|
π |
π |
=ϕ . |
(5.82) |
|||||||
− ωt −ψ+ |
2 |
= ψ− |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отметим, что разность фаз ∆ϕВНЕШ, I |
для цепей переменного тока обозначают |
|||||||||||||
буквой ϕ : ∆ϕВНЕШ, I |
=ϕ . |
|
|
|
|
|
|
|
|
|
||||
|
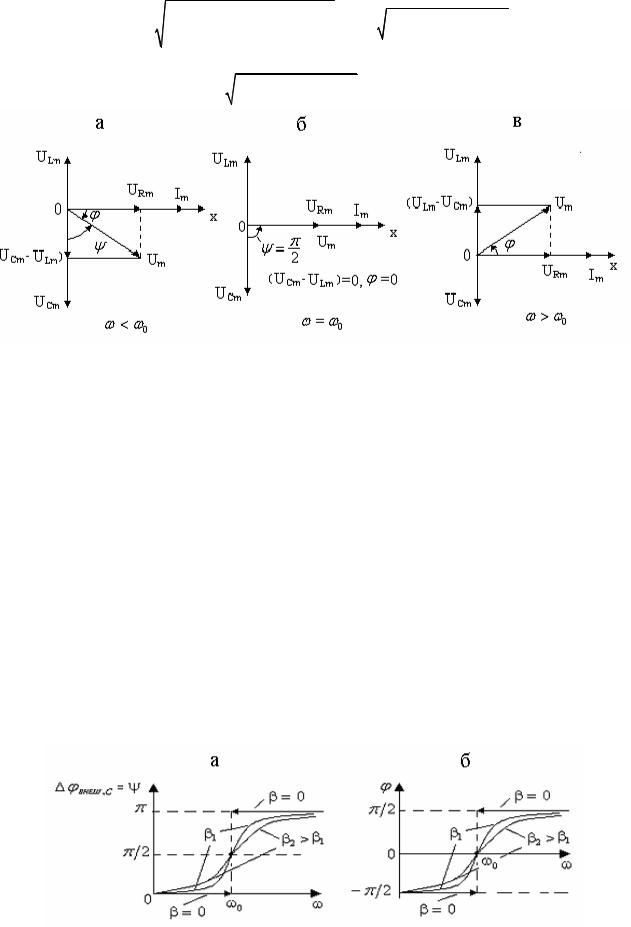
На рис. |
5.21 |
приведены фазовые |
резонансные кривые |
∆ϕВНЕШ,С (ω) и |
|||||||||
∆ϕ |
ВНЕШ, I ( |
ω =ϕ |
ω , |
построенные по формулам (5.66) |
|
и (5.82) |
|
при значениях |
||||||
|
) |
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
параметра в : |
β= 0, β2 >β1 ≠ 0 . |
|
|
|
|
|
|
|
|
|
||||
Рис. 5.21
35

Из них следует, что внешнее напряжение опережает по фазе напряжение на конденсаторе на угол ψ . На векторной диаграмме это означает, что вектор амплитуды Um располагается выше вектора амплитуды UCm (рис. 5.20 а,б,в). Причем угол ш изменяется от нулевого значения для частоты щ, равной нулю ( ω= 0 ), до значения равного р при частоте внешнего напряжения стремящегося к бесконечности ( ω→ ∞ , рис. 5.21,а). При резонансе амплитуды векторов внешнего напряжения Um и напряжения на конденсаторе UCm взаимно перпендикулярны (см. рис. 5.20,б), что приводит к разности фаз между ними,
равной π2 ( ∆ϕВНЕШ, C = ψ= π2 , Рис. 5.21,а).
Из другой фазовой резонансной кривой следует, что фаза внешнего
напряжения для частот ω> ω0 |
отстает от фазы тока в контуре на угол ϕ |
(рис.5.21,б). Для частот ω> ω0 |
фаза внешнего напряжения опережает на угол ϕ |
фазу колебаний силы тока в контуре и при увеличении частоты щ стремится к значению, равному р2 . При резонансе ( ω= ω0 ,.UCm =ULm ) фаза колебаний силы
тока и внешнего напряжения совпадают, т.е. ϕ(ω0 )= 0 и вектора амплитуд Um и Im направлены одинаково, вдоль оси Ox (рис. 5.21,б).
При этом энергия поступает в контур согласованно с колебаниями в ней. Действительно, учитывая выполнение условий малого затухания (Q >>1) и формулы (5.64) и (5.66) запишем
ω= ω ω : |
tgψ= |
2βωp |
|
= |
ωp |
1 ψ |
π |
; |
||
ω2 |
−ω2 |
β |
2 |
|||||||
p 0 |
|
|
|
|
||||||
|
|
0 |
p |
|
|
|
|
|
||
I = −Im sin(ωt −ψ) = Im cosωt , |
|
UВНЕШ =Um cosωt . |
||||||||
Такое поступление энергии в контур при резонансе приводит к большим амплитудам колебаний, их числовые значения определяются диссипацией (рассеянием) энергии системы, т. е. коэффициентом затухания β (формула
(5.70)). |
частотах ω, больших или меньших ω0 ( ω< ω0 , ω< ω0 ) амплитуда |
При |
вынужденных колебаний даже в отсутствии диссипации энергии (β= 0 ) будет уменьшаться, она определяется расстройкой резонанса ( ω−ω0 ), т.е. разностью
частот ω и ω0 .
Можно отметить, что с использованием таблицы аналогий можно построить фазовые резонансные кривые для разности фаз между скоростью колебаний тела и действующей на него внешней силой в случае механической системы и т.д.
36
5.10.5. Переменный электрический ток
Переменный электрический ток также представляет собой вынужденные колебания силы тока, напряжения, происходящие в электрической цепи под действием напряжения, вырабатываемого генератором переменного тока на электростанциях. Электрическая цепь в этом случае представляет собой колебательный контур (см. рис. 5.3, UВНЕШ =Um cosωt ) и поэтому здесь
применимы формулы, которые были получены в § 5.10.1 – § 5.10.4.
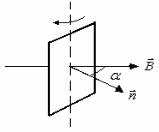
Простейшей моделью генератора переменного тока является рамка площади S, содержащая N витков, которая вращается равномерно в магнитном поле с угловой частотой ω (рис. 5.22). Для максимальной ЭДС
индукцииεim , наводимой в такой рамке, можно получить
следующее выражение:
Рис. 5 22
εi = −NФ′ = −N (BS cos ωt )′ = NBSωsinωt , εim = NBSω. (5.83)
Отметим, что линейная частота переменного тока в России составляет 50 Гц. Перечислим вопросы и понятия, которые вводят для описания
переменного тока в электрической цепи.
1.Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении электрической цепи.
Как уже было отмечено раньше (см. § 5.10.4), фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π/2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π/2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают.
2.Емкостное XC, индуктивное XL, активное R, реактивное X и полное Z
сопротивления цепи. В соответствии с законом Ома для однородного участка
цепи по формулам (5.67) можно ввести емкостное XC и индуктивное XL сопротивления
Im = ωqm , URm = RIm ,
U |
|
= |
qm |
= |
1 |
( |
q |
ω = X I |
|
|
, |
|
U |
|
= Lq ω2 = |
( |
ωL |
)( |
q ω = X I |
|
|
|||||
|
|
ωC |
|
|
|
|
|
|||||||||||||||||||
|
Cm |
|
C |
m |
) |
|
c |
m |
1 |
|
|
Lm |
|
m |
|
|
m ) |
L |
m |
|
||||||
|
|
|
|
|
|
|
|
X |
c |
= |
|
|
, |
|
|
X |
|
= ωL . |
|
|
|
|
(5.84) |
|||
|
|
|
|
|
|
|
|
|
ωC |
|
|
L |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Они характеризуют способность катушки и конденсатора оказывать препятствие протеканию переменного электрического тока. Как видно из формул (5.84), при возрастании частоты переменного тока емкостное сопротивление XC будет уменьшаться, т.е. конденсатор оказывает меньшее препятствие протеканию тока, а индуктивное сопротивление XL будет
37
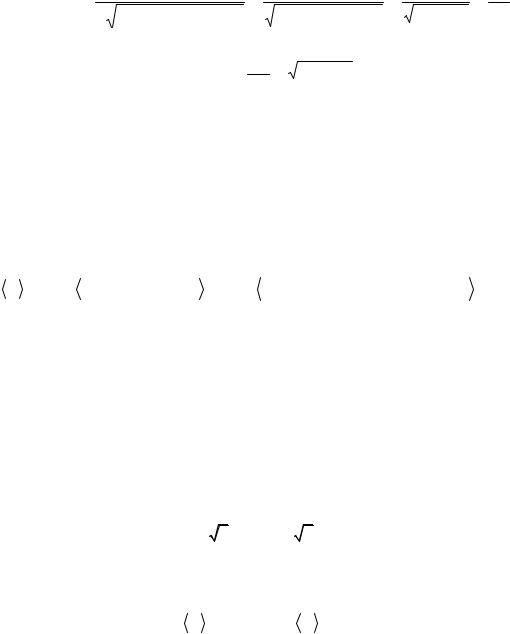
возрастать - катушка оказывает большее препятствие протеканию переменного тока. Постоянный ток через участок цепи, содержащий конденсатор, не протекает ( ω =0: XC = ∞). Индуктивное сопротивление
катушки в этом случае будет равно нулю ( ω =0: X L = 0 ), т.е. катушка не
оказывает препятствия протеканию постоянного тока. Сопротивление R, которое было введено ранее в разделе постоянный ток, называется здесь активным сопротивлением.
Учитывая введенные сопротивления, перепишем формулу (5.68) для резонансной кривой амплитуды силы тока в контуре следующим образом:
Im = |
ωUm |
= |
Um |
= Um |
= Um , |
|
L (ω02 −ω2 )2 + 4β2ω2 |
|
(X L − XC )2 + R2 |
X 2 + R2 |
Z |
где введены реактивное X и полное Z сопротивления цепи
X = X L − XC |
, Z = |
Um = X 2 + R2 . |
(5.85) |
|
|
Im |
|
3. Мощность, потребляемая электрической цепью. Учитывая разность фаз колебаний силы тока и внешнего напряжения в электрической цепи
ϕ = (ϕВНЕШ − ϕI ) = (ωt − (ωt − ψ + π2 )) = ψ − π2 ,
для мгновенной мощности, потребляемой электрической цепью, получим
P = IUВНЕШ = ImUm cosωt cos(ωt −ϕ) .
Ввиду малого периода колебаний переменного тока (T = 0.02 c ) многие приборы измеряют усредненные по времени значения мощности
P = ImUm cos ωt cos(ωt −ϕ) |
= ImUm cos2 ωt cosϕ +sinωt cosωt sinϕ |
= |
||||||
= |
1 |
ImUm cosϕ . |
|
|
|
(5.86) |
||
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
Согласно векторной диаграмме (см. Рис. 5.21,а,б,в) |
|
|||||||
|
|
Um cosϕ = URm = Im R , |
(5.87) |
|||||
что приводит к следующему выражению для усредненной мощности |
||||||||
P = |
1 |
ImUm = |
1 |
Im |
2 R . |
(5.88) |
||
|
2 |
|||||||
|
|
2 |
|
|
|
|
||
4. Эффективные (действующие) значения силы тока и напряжения. Эти величины для гармонических колебаний вводятся по формулам
IЭФ = |
Im |
, |
UЭФ = |
Um |
. |
(5.89) |
2 |
|
|||||
|
|
2 |
|
|
||
Их введение позволяет переписать формулу (5.88) без коэффициента ½, что является удобным при записи формул для средней мощности и количества теплоты в случаях переменного и постоянного тока
P = I U |
, |
P = I 2 |
Rt . |
ЭФ ЭФ |
|
ЭФ |
|
Отметим, что многие амперметры и вольтметры измеряют эффективные (действующие) значения силы тока и напряжения.
5. Коэффициент мощности. Входящий в формулу (5.86) коэффициент cosϕ называют коэффициентом мощности. В соответствии с выражениями (5.85) и (5.87) для него можно записать
38
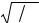
cosϕ = |
R |
, |
(5.90) |
|
Z
т.е. он равен отношению активного R и полного Z сопротивлений электрической цепи.
Коэффициент мощности показывает зависимость мощности, выделяемой в электрической цепи переменного тока, от разности фаз колебаний силы тока в
ней и внешнего напряжения, поступающего в цепь. Так, |
если |
реактивное |
сопротивление цепи будет равно нулю ( X = 0 , Z = R ), то |
тогда |
cosϕ =1 и |
электрическая цепь полностью потребляет поступающую в нее энергию. При отсутствии же в цепи активного сопротивления (R=0, cosϕ =0) электрическая цепь энергии не потребляет. Это приводит к тому, что энергия, поступающая в цепь, передается по проводам обратно к источнику энергии, что приводит к ее потерям в подводящих проводах за счет выделения джоулевого тепла. На практике стремятся увеличить cosϕ до максимально возможных значений
(обычно cosϕ >0,85).
5.10.6. Энергетика резонанса. Некоторые примеры проявления и применения резонанса в природе и технике
При резонансе энергия поступает в систему согласованно с колебаниями в ней, постоянно увеличивая их амплитуду. В стационарном режиме большая амплитуда колебаний поддерживается малыми поступлениями энергии в систему, восполняющими потери энергии колебаний (нагрев проводников, преодоление сил сопротивления, потери на излучение электромагнитных и механических волн) за один период. В системе при резонансе созданы наиболее благоприятные условия для реализации свойственных системе свободных незатухающих колебаний, и поэтому амплитуда колебаний резко возрастает.
Рассмотрим некоторые примеры проявления резонанса в природе. Пример 1. Солдаты проходят по мосту строевым шагом, частота ударов ног о поверхность моста может совпасть с собственной частотой колебаний моста как колебательной системы, наступает явление резонанса, при котором амплитуда колебаний моста постепенно нарастает и при больших числовых значениях может привести к его разрушению.
Пример 2. Вентилятор плохо прикреплен к потолку и при своем вращении он создает толчки на потолок, частота которых может совпасть с собственной частотой колебаний комнаты (потолка) как колебательной системы, амплитуда колебаний потолка нарастает и может привести к его обрушению.
Пример 3. Приборы на кораблях максимально утяжеляют (делают тяжелыми подставки) и подвешивают на мягких пружинах (коэффициент жесткости для них будет малым). В этом случае частота качки ωК корабля будет больше
собственной частоты колебаний ( ω0 = к m ) приборов на пружинах и поэтому резонанса не наступает.
39
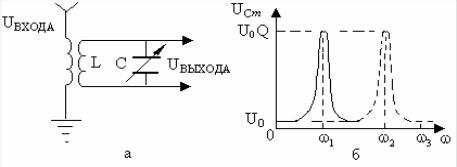
Пример 4. В радиоприемниках на основе явления резонанса можно выделить нужный сигнал из большого числа сигналов разных радиостанций, поступающих на его приемную антенну (рис. 5.23,а). Пусть на вход радиоприемника поступают сигналы малой амплитуды с различной несущей частотой ω
UВХОДА =Um1 (ω)cos(ω1t )+Um2 (ω)cos(ω2t )+Um3 (ω)cos(ω3t )+...
Для выделения сигнала с несущей частотой ω1 , необходимо добиться равенства частоты ω0 собственных свободных незатухающих колебаний приемного контура и частоты ω1 ( ω0 = ω1 ). Тогда за счет явления резонанса амплитуда сигнала с частотой ω1 на выходе конденсатора резко возрастает, а амплитуды остальных сигналов останутся прежними (рис. 5.23,б показана сплошной линией резонансная кривая, максимум которой приходится на частоту ω1 )
Рис. 5.23
UВХОДА =UC = QUm1 (ω)cos(ω1t )+Um2 (ω)cos(ω2t )+Um3 (ω)cos(ω3t )+...≈ QUm1 (ω)cos(ω1t ) ,
и тем самым происходит выделение сигнала с несущей частотой ω1 . Изменяя электроемкость конденсатора, можно настроить приемный контур антенны на несущую частоту ω2 (на рис. 5.22,б пик резонансной кривой смещается на частотуω2 ).
5.11.Нелинейные системы. Автоколебания
1.Нелинейные системы. Под нелинейными системами понимают такие колебательные системы, свойства которых зависят от происходящих в них процессов. В таких системах существуют нелинейные связи, например, между:
1)силой упругости FУ и смещением x груза относительно положения
равновесия. Это приводит к нарушению закона Гука и к зависимости коэффициента к жесткости системы от смещения x , что изменяет собственную частоту ω0 колебаний системы; 2) электрическими зарядами конденсатора и
создаваемой ими напряженностью поля (сегнетоэлектрик между пластинами
40
