Волны

Федеральное агентство по образованию ГОУ ВПО “Уральский государственный технический университет – УПИ”

М.Г. Валишев, А.А. Повзнер

ФИЗИКА

Часть 4

КОЛЕБАНИЯ И ВОЛНЫ

Учебное пособие

Научный редактор – проф., д-р физ.-мат. наук Ф.А. Сидоренко

Екатеринбург

2006

6.2.1.Волновые уравнения для электромагнитной волны (ЭМВ). Уравнение плоской

6.2.3.Давление ЭМВ. Опыты П.Н. Лебедева, подтверждающие электромагнитную

6.2.6.Ударные волны. Уединенные волны………........................................................... 87

4

5. ТЕОРИЯ КОЛЕБАНИЙ

5.1. Введение

Различные виды движений и процессов, происходящих в природе, можно классифицировать по-разному. По одной из таких классификаций принято выделять колебательные движения (колебания), частный случай колебательных движений – периодические колебания, и самый простой вид периодических колебаний – это гармонические колебания.

К колебательным движениям (колебаниям) относят такие движения,

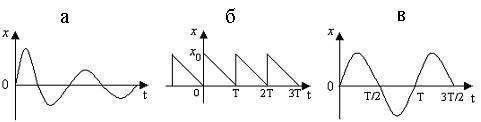
которые характеризуются той или иной степенью повторяемости во времени описывающих их величин. К колебательным процессам можно, например, отнести механические колебания груза пружинного и математического маятников, автоколебания голосовых связок при разговоре, электромагнитные колебания силы тока, заряда, напряжения, вектора магнитной индукции В магнитного поля катушки в колебательном контуре, периодические колебания цвета продуктов некоторых химических реакций и т.д. На Рис. 5.1,а в качестве примера колебательного движения приведена зависимость от времени t смещения х груза (материальной точки) пружинного маятника от положения равновесия.

Рис .5.1

К периодическим колебаниям относят колебания, при которых

описывающие их величины повторяются через промежуток времени, называемый периодом Т (рис. 5.1,б). При гармонических колебаниях (ГК)

эти величины изменяются по гармоническому закону, т.е. по закону синуса или косинуса (рис. 5.1,в).

ГК, как наиболее простые колебания, играют особую роль среди других видов колебаний. Оказывается, что при достаточно общих условиях, которые обычно выполняются в физических задачах, любой сложный процесс, описываемый какой-либо периодической или непериодической функцией времени f(t), можно представить в виде совокупности конечного или бесконечного набора гармонических колебаний разной частоты, т.е. представить его в виде ряда или интеграла Фурье (см. § 5.8).

5

Это позволяет, например, предложить общую методику анализа различных временных процессов по их частотному спектру, методику воздействия сигналов на любые системы по изменению их частотного спектра и т.д.

Между различными видами колебаний, такими как механические, электромагнитные, химические и т.д., происходящих в замкнутых и открытых системах, существуют много общего. Поэтому, в этом разделе наряду с рассмотрением отдельных видов колебаний изучается и то, что их объединяет, а именно: общие для них понятия (период Т, амплитуда А, фаза колебаний φ и

т.д.), дифференциальные уравнения и их решения. В связи с этим широкое применение в этом разделе находит метод аналогий, при котором результаты, полученные при рассмотрении одного вида колебаний, используются для описания и других видов колебаний.

5.2. Условия возникновения колебаний в системе. Таблица аналогий между механическими и

электромагнитными колебаниями

Рассмотрим подробнее аналогию между наиболее часто встречающимися в природе механическими и электромагнитными колебаниями. Для этого обсудим подробно электромагнитные колебания, происходящие в идеальном колебательном контуре (отсутствуют потери энергии колебаний на нагревание проводников), и механические колебания груза (материальной точки) пружинного маятника в отсутствии сил трения и сопротивления.

Пусть в начальный момент времени (t=0, состояние 1) груз пружинного маятника максимально отклонен от положения равновесия (х=хm, рис. 5.2,а), а на обкладки конденсатора колебательного контура сообщают максимальный заряд (q=qm, рис. 5.2,б).

Состояние 1 пружинного маятника характеризуется тем, что скорость груза и его кинетическая энергия равны нулю, а полная энергия колебаний равна максимальной потенциальной энергии пружины. Для колебательного контура в состоянии 1 сила тока и энергия магнитного поля катушки равны нулю, а полная энергия колебаний совпадает с максимальной энергией электрического поля конденсатора.

t=0, Состояние 1. Пружинный маятник:

В течение времени 0< t< T/4 происходят следующие процессы. Пружинный маятник. Под действием силы упругости груз начинает двигаться, скорость груза нарастает постепенно из-за наличия у него инерционных свойств (массы) и в момент времени t, равный четверти периода колебаний Т

6

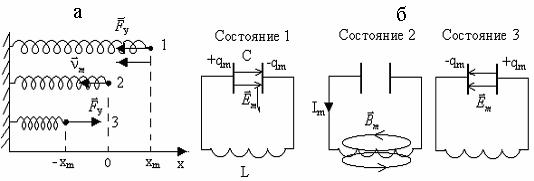
(t=T/4) груз проходит положение равновесия (состояние 2, рис. 5.2,а). При этом потенциальная энергия пружины полностью переходит в кинетическую энергию груза.

Колебательный контур. Конденсатор начинает разряжаться, сила тока в кон-

Рис. 5.2

туре возрастает постепенно из-за возникновения в катушке Э.Д.С. самоиндукции, которая препятствует нарастанию основного тока в контуре. Сила тока достигает максимального значения в момент времени t=T/4 (состояние 2, рис. 5.2,б). При этом энергия электрического поля конденсатора полностью переходит в энергию магнитного поля катушки.

t=Т/4, Состояние 2. Пружинный маятник:

В следующие четверть периода (T/4< t< T/2) наблюдаются такие процессы. Пружинный маятник. Под действием силы упругости скорость груза начинает уменьшаться, она уменьшается постепенно из-за наличия у груза массы и в момент времени t= T/2 (состояние 3, рис. 5.2,а) она обращается в ноль, кинетическая энергия груза полностью переходит в потенциальную энергию сжатой пружины.

Колебательный контур. Сила тока в контуре начинает убывать, убывает она постепенно, так как в катушке возникает ток самоиндукции, который препятствует убыванию основного тока в контуре, и в момент времени t= T/2 (состояние 3, рис. 5.2,б) сила тока обращается в ноль. Конденсатор перезаряжается, энергия магнитного поля катушки полностью переходит в энергию электрического поля конденсатора.

t=Т/2, Состояние 3. Пружинный маятник:

7

Из описанных выше колебательных процессов можно сделать вывод об условиях возникновения колебаний в любой системе, а именно: система должна обладать 1) устойчивым положением равновесия; 2) инерционными свойствами; 3) малыми потерями энергии колебаний (на преодоление сил трения в случае механических колебаний и на нагревание проводников в случае электромагнитных колебаний в контуре).

Рассмотренные примеры позволяют установить аналогию между механическими и электромагнитными колебаниями, которая отражена в табл.5.1

С помощью данной таблицы можно записывать формулы для одного вида колебаний, если известны аналогичные формулы для другого вида колебаний. Так, например,

В дальнейшем эта таблица будет использоваться для записи без вывода различных формул теории колебаний.

5.3. Общие дифференциальные уравнения, описывающие колебания в произвольной системе

Выведем общее дифференциальное уравнение, описывающее достаточно широкий круг происходящих в системе колебаний. Для этого рассмотрим открытый колебательный контур, в который подается внешнее напряжение U ВНЕШ и имеются потери энергии

на нагревание проводников (рис. 5.3).

Из закона сохранения энергии следует, что элементарная работаAВНЕШ тока, поступающего в контур извне, расходуется на изменение энергии колебаний dW и на нагревание проводников dQ :

Рис. 5.3

dW +dQ = AВНЕШ .

8

Распишем это выражение

Буквой β в формуле (5.2) обозначен коэффициент затухания колебаний, а величина ω0 в формуле (5.3) называется циклической (круговой) частотой

свободных незатухающих гармонических колебаний контура. Свободные незатухающие колебания происходят в выведенной из состояния равновесия замкнутой системе (нет поступления энергии извне), в которой отсутствуют потери энергии колебаний (β=0).

Уравнение (5.1) описывает различные случаи колебаний в открытом и закрытом колебательных контурах. Для получения аналогичного уравнения, описывающего колебания в механической системе, воспользуемся табл. аналогий 5.1:

где FВНЕШ – проекция вектора внешней силы на ось Ох, вдоль которой происходят колебания.

Рассмотрим частные случаи решения уравнений (5.1) и (5.4).

5.4. Механические незатухающие гармонические колебания в замкнутой системе

Для замкнутой системы ( FВНЕШ =0), в которой отсутствуют потери энергии на преодоление сил сопротивления или трения (β=0), дифференциальное уравнение (5.4) примет вид

9

Из теории дифференциальных уравнений следует, что решением этого уравнения (его называют однородным линейным дифференциальным уравнением второго порядка) является гармоническое колебание

т.е. смещение х тела (материальной точки) от положения равновесия изменяется по гармоническому закону. В уравнении (5.7) введены такие понятия, как

хm – максимальное смещение или амплитуда колебания. В общем случае под амплитудой колебаний понимают положительную величину, стоящую перед знаком синуса или косинуса;

ϕ = (ω0t + ϕ0 ) -–фаза колебаний – величина, стоящая под знаком синуса

или косинуса; ϕ0 – начальная фаза колебаний – фаза колебаний в начальный момент

времени t=0;

ω0 – циклическая (круговая) частота свободных незатухающих

гармонических колебаний системы, определяемая свойствами системы по формуле (5.5).

Циклическая частота ω0 связана с периодом колебаний Т и линейной

Запишем выражения для проекций скорости, проекции ускорения тела (м.т.) на ось Ох, потенциальной, кинетической и полной энергий тела, совершающего гармонические колебания

изменяются по гармоническому закону подобно ее смещению х, а полная энергия W колебаний м.т. остается при этом неизменной.

Приведем в пределах одного периода Т колебаний графики зависимости х, υX , aX ,WK, WP и W от времени t для м.т. при ее гармонических колебаниях

10