Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Формулы ТВ

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

212.86 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ФОРМУЛЫ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ

	A , a Î A содержит n элементов,
Правила сложе-	B , b Î B – m элементов.
ния и умножения	Выбор “ a или b ” можно осуществить n + m способами,
	выбор “ a и b ” – n ´ m способами
	Выборки без возвращения
Число перестановок n элементов		Pn = n!
Число размещений из n по m (m £ n)		Anm =		n!
Число размещений из n по m (m £ n)		Anm =		(n - m)!
				(n - m)!
Число сочетаний из n по m (m £ n)		Cnm =		n!
Число сочетаний из n по m (m £ n)		Cnm =	m!×(n - m)!
			m!×(n - m)!

Выборки с возвращением (с повторениями)

Число размещений с повторениями из n по m			%m			= n	m
Число размещений с повторениями из n по m			An			= n
Число сочетаний с повторениями из n по m			% m			m
Число сочетаний с повторениями из n по m			Cn	= Cn+m-1
Пусть n –элементное множество состоит из эле-
ментов k различных типов, причем 1–й элемент
повторяется n1 раз, 2–й элемент – n2 раз,…, k –й						n!
– nk раз и n1 + n2 + ...+ nk = n . Перестановки n	Pn (n1	,n2	,...,nk ) =			n!
элементов данного множества называются пере-	Pn (n1	,n2	,...,nk ) =		n1!×n2!×...×nk!
элементов данного множества называются пере-					n1!×n2!×...×nk!
становками с повторениями.
Число перестановок из n элементов с
повторениями по n1 , n2 , …, nk

СЛУЧАЙНЫЕ СОБЫТИЯ

ОСНОВНЫЕ ПОНЯТИЯ

Испытание (опыт)

Совокупность условий, которые могут повторяться произвольное количество раз

Событие (исход) Результат испытания

КЛАССИФИКАЦИЯ СОБЫТИЙ

	Достоверное (Ω)			Обязательно произойдет
	Невозможное (Ø)			Не может произойти
	Случайное (А, В, С,…)			Может произойти или не произойти
				Обязательно произойдет, если не
	Противоположное ( A)			Обязательно произойдет, если не
	Противоположное ( A)			произойдет А
				произойдет А
	Элементарное событие			Неделимое на более простые события
	(элементарный исход)			в условиях данного опыта
	Совместные			Появление одного не исключает по-

326

P( A) =

		явление других
	Несовместные	Появление одного исключает появле-
	Несовместные	ние других
		ние других
	Равновозможные	Нет оснований считать какое-то более
	Равновозможные	возможным, чем другие
		возможным, чем другие
		Несовместные, в совокупности ис-
	Полная группа событий A1 , A2 ,...An	черпывающие все возможные исходы
		A1 + A2 + ...+ An = W , Ai Aj = Æ, i ¹ j
	Пространство элементарных исходов	Полная группа элементарных исходов

ВЕРОЯТНОСТЬ

Вероятность события P (A) – численная мера степени возможности появ-

ления события А, 0 £ P (A) £1.

ВАРИАНТЫ ОПРЕДЕЛЕНИЙ ВЕРОЯТНОСТИ

Статистическое определение вероятности

Число, около которого группируются относительные частоты при увеличении числа испытаний, называется статистической вероятностью рассматриваемого события.

Относительной частотой W ( A) события А называют отношение числа испытаний m, в которых событие А появилось, к числу всех проведенных испы-

таний n: W (A )= mn .

Классическое определение вероятности

Пусть пространство элементарных событий W состоит из конечного числа равновозможных элементарных исходов.

n , где m – число благоприятствующих исходов, n – общее число несо-

вместных равновозможных исходов, составляющих пространство исходов.

Геометрическое определение вероятности

Используется, если число равновозможных исходов бесконечно и несчетно. Пусть каждый результат испытаний определяется случайным положением точки в некоторой области W (отрезок линии, фигура на плоскости, тело в

пространстве), мера которой m(W) (под мерой области будем понимать длину, площадь, объем). Наступлению события А благоприятствует попадание

точки в область A Í W. Вероятность события А: P(A )= m(A) , где m(A) -

m(W )

мера области А.

327

Аксиоматическое определение вероятности

Если событие не обладает симметрией возможных исходов, ероятности нельзя вычислить по классической формуле. В этом случае используется аксиоматический теоретико-множественный подход: рассматривается пространство исходов W; каждому исходу или множеству исходов A Í W , соответствующему некоторому событию А, ставится в соответствие вероятность события P ( A) – число, удовлетворяющее следующим условиям:

1)Вероятность любого события заключена между 0 и 1: 0 £ P( A) £1.

2)Вероятность достоверного события P (W) = 1.

3)Если А и В – несовместные события ( A × B = Æ ), то P( A + B) = P( A) + P(B)

или для любого числа событий A1, A2 ,K, An , если Ai × Aj = Æ при i ¹ j , то

P çæ	n		n
	åAi ÷ö		= åP (Ai ), т.е. вероятность суммы несовместных событий равна
è i =1		ø	i =1

сумме вероятностей этих событий. A1, A2 ,K, An , или, для счетного множества несовместных событий A1, A2 ,K, An ,K( Ai × Aj = Æ, i ¹ j) ,

P çæ	¥		¥
	åAi ÷ö		= åP (Ai ).
è i=1		ø	i =1

Следствия:

1.Вероятность невозможного событияP (Æ) = 0 .

2.Если A Í B (событие А влечет за собой событие В), то P( A) £ P(B) .

3.Если события A и A противоположны, P(A) + P( A) =1.

4. Если события A1, A2 ,K, An образуют полную группу несовместных собы-

n	n
тий, т.е. если åAi = W, ( Ai × Aj = Æ,	i ¹ j), то åP( Ai ) =1.
i=1	i=1
Теорема сложения вероятностей

Если события А и В совместны, A × B ¹ Æ , то Для несовместных событий А и В: P( A + B) = мы трех совместных событий А, В и С:

P (A + B + C ) = P (A) + P (B ) + P (C )- P (AB )

P(A + B) = P(A) + P(B) - P(AB) .

P( A) + P(B) . Вероятность сум-

- P (AC ) - P (BC ) + P (ABC ).

Условная вероятность события А,	при	P (B	A) =	P (AB )

условии, что событие В произошло					,P (A )¹ 0.
				P (A )

Теорема умножения вероятностей		P (AB ) = P (A)× P (B				A),

		P (AB ) = P (B )× P (A				B)

Для произвольного числа событий

P (A1 × A2 ×...× An ) = P (A1 )× P (A2 A1 )× P (A3 A1 × A2 )×...× P (An A1 × A2 ×...× An-1 ).

328

События А и В независимы, если вероятность события А не зависит от того, произошло событие В или нет, т.е., P (A B) = P (A). В противоположном слу-

чае, если P (A B) ¹ P (A), события А и В зависимы.

Для независимых событий Р(А·В)=Р(А)·Р(В).

Для нескольких независимых событий Р(А1·А2·…·Аn)=Р(А1)·Р(А2)·…·Р(Аn), или

P çæ	n		n
P çæ	Õ Ai ÷ö		= ÕP (Ai ),
è	i =1	ø	i =1

Формула полной вероятности

Событие A может произойти только вместе с одним из n взаимоисключающих событий (гипотез) H1 ,H2 ,...,Hn , образующих полную группу:

H1 + H2 + ...+ Hn = W , Hi H j = Æ (i ¹ j).

Известны вероятности реализации гипотез:

P(H1 ), P(H2 ),..., P(Hn ) , åP(Hi ) = 1

i=1

и условные вероятности события А при реализации каждой из гипотез:

P(A|H1), P(A|H2),…,P(A|Hn).

(

i )

Полная вероятность события А: P

(

)

(

)

× P

Формула Бейеса (теорема гипотез)

Вероятности гипотез P(H1 ), P(H2 ),..., P(H n )

заданы до наступления

события А. После того, как произошло событие А, вероятности гипотез изменяются из-за получения дополнительной информации, что событие А про-

изошло: Р(Н1|А), Р(Н2|А),…, Р(Нn|А).


P (Hi	A) =	P (Hi )P (A		Hi )			i =1, 2..., n .


						,
		n				,
		åP (Hi	)P (A		Hi )
		åP (Hi	)P (A		Hi )

i=1

Повторение опытов. Формула Бернулли

Рассмотрим сложный опыт, состоящий из нескольких независимых простых испытаний. Вероятность появления события А в каждом из них

P (A) = p , вероятность противоположного события P (A) = 1 - p = q .

Вероятность появления события А m раз в серии из n независимых опытов (формула Бернулли):

Pn (m) = Cnm pmqn-m =	n!	pm (1- p)n-m .
	m!(n - m)!

329

Вероятность того, что в n испытаниях событие А наступит

менее m раз:

Pn (0) + Pn (1) +...+ Pn (m -1) ,

более m раз:

Pn (m +1) + Pn (m + 2) +... + Pn (n) ,

не менее m раз:

Pn (m) + Pn (m +1) +... + Pn (n) ,

не более m раз:

Pn (0) + Pn (1) +... + Pn (m) .

Предельные случаи формулы Бернулли

Предельные теоремы Муавра - Лапласа

Вероятность P n (m)

того, что при n независимых испытаниях событие А

появляется m раз при больших n

(m )»

1 j(x )

x =

- np

, j( x) =

× е-

– функция Гаусса.

npq

, где

npq

Вероятность того, что событие А наступит в n испытаниях не менее m1 раз,

но не более m2 раз:

- np

(m ,m

) » Ф (x ) -Ф (x ), x1 =

, x2 =

1 2

npq

Ф (x )=

òe-

dz – функция Лапласа.

Теоремы Муавра-Лапласа используют, если p и q не малы, а npq > 9 .

Формула Пуассона

n (

m »

lme-l

, где

l = np

( n

10 , p

0,1,

9 ).

)

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Пусть W = w

– пространство элементарных событий. Случайная величина

{

}

(с.в.)

X – функция X (w), определенная на множестве W , принимающая чи-

словые значения и такая, что для любого x Î R определена вероятность

P (X < x)

= P w

: X (w) < x

}

Эта вероятность P(X <x) =F(x)

{

называется функцией распределения с.в. X .

0 £ F (x ) £ 1

Свойства функции распределения

P{a £ X < b} = F (b)- F (a )

F (x1 ) £ F (x2 ), если x1 < x2 ;

F (-¥) = 0, F (¥) = 1

330

Для дискретной с.в. X , принимающей значения x1, x2 ,... с вероятностями p1, p2 ,... функция распределения

F (x) = P{X < x} = å pi ,

xi <x

где суммируются вероятности тех значений xi , которые меньше x . Для непрерывной с.в. X функция распределения

F (x )= ò f (t )dt ,

-¥

где f (x) – плотность распределения (плотность вероятности).

				1		f (x ) ³ 0
						¥	f (x )dx = 1
				2		ò	f (x )dx = 1
Свойства плотности вероятности						-¥
Свойства плотности вероятности				3		f (x ) = F ¢(x )
				3		f (x ) = F ¢(x )
								b
				4		P{a < X < b}= ò f (x )dx
								a
Рядом (или законом) распределения дискретной с.в. X называют таблицу
вида
	X	x1	x2		x3		…
	P	p1	p2		p3		…

Числовые характеристики случайных величин

Характеристики положения с.в. – математическое ожидание, мода и медиана.

Математическое ожидание (среднее значение) случайной величины X

n	¥
M (X )= åxi pi = mx	mx = M (X )= ò x × f (x)dx
i=1	-¥
(для дискретной с.в.)	(для непрерывной с.в.)

Свойства математического ожидания

1)M (C ) = C , C - const ;

2)M (CX ) = CM (X ) ;

3)	M (X ± Y ) = M (X ) ± M (Y ) , X и Y – любые с.в.;
4)	M (X ×Y ) = M (X ) × M (Y ) , если X и Y – независимые с.в.

С.в. называются независимыми если для любых x и y имеет место равенст-

во P{X < x,Y < y} = P {X < x}× P {Y < y}.

331

Мода Mox дискретной с.в.– ее	Мода непрерывной с.в.– значение, при ко-
наиболее вероятное значение	тором плотность вероятности максимальна

Медиана Mex непрерывной с.в. – такое значение с.в., для которого

P{X < Mex }= P{X > Mex }= 2 .

Характеристики рассеяния с.в. относительно среднего значения – дисперсия и среднее квадратичное отклонение (СКО).

Дисперсия случайной величины X :	D (X )= Dx = M ((X - mx )2 );
Для вычислений удобна формула:	Dx = M (X 2 )- (mx	2).

n	¥
n	Dx = ò (x - mx )2 f (x )dx
Dx = å(xi - mx )2 pi	Dx = ò (x - mx )2 f (x )dx
i =1	-¥
(для дискретной с.в.)	(для непрерывной с.в.)

Свойства дисперсии

1)D (C ) = 0 , C - const ;

2)D (CX ) = C2 D (X );

3)D (X ±Y ) = D (X ) + D (Y ) , X и Y – независимые с.в.

Среднее квадратическое отклонение (СКО): s (X ) = s 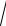x = Dx .

Моменты случайных величин

									n
							as (X )= åxis pi
Начальный момент порядка s								i=1
Начальный момент порядка s							(для дискретной с.в.)
с.в. Х – математическое ожидание							(для дискретной с.в.)
с.в. Х – математическое ожидание
с.в. X s :			as (X ) = M (X s ).				¥	x	s	f (x )dx
							as (X )= ò	x		f (x )dx
							-¥
							(для непрерывной с.в.)

							n
							as (X )= å(xi - mx )s pi
Центральный момент порядка s							i =1
Центральный момент порядка s							(для дискретной с.в.)
с.в. Х :			(	(X - M (X )s	)
m	s	(X )= M		(X - M (X )s		.	¥
	s						as (X )= ò (x - mx )s f (x )dx
							-¥
							(для непрерывной с.в.)

332

Основные законы распределения случайных величин

и их числовые характеристики

Название

Формула

M ( X )

D (X )

Примечания

Биномиаль-

Pn (X = k ) = Cnk pk qn -k

npq

0 £ k £ n

ное распре-

деление

Распределе-

P (X = k ) =

ние Пуассо-

e-l

на

Равномер-

ì 0, x

< a, x > b,

ì0, x < a,

b + a

(b - a )

- a

ное распре-

f (x) =

F ( x) =

ï x

, a

£ x £ b ,

деление

, a £ x £ b.

ïb - a

îb - a

ï1,

x > b.

Показатель-

-l x

, x ³ 0,

-l x

, x

ное распре-

f (x) = í

F ( x) =

деление

î0, x < 0,

î0, x < 0.

Нормальное

(x-m )2

распределе-

f (x )=

F (x )=

æ х - m ö

2s 2

ние

+Ф ç

N (m,s )

Стандарт-

ное нор-

F (x )=

+Ф (x )

мальное

f ( x ) =

e 2

распределе-

ние N (0,1)

Сумма квадратов независимых с.в.

Х1 , Х 2 ,..., Х n , распределенных

по стандартному нормальному закону N (0,1) распределена

по

Распределе-

закону, называемому «хи – квадрат с n степенями свободы»:

ние c2

c 2 = åX i2 .

(Пирсона)

i=1

Если эти величины связаны одним линейным соотношением, на-

пример, åXi =nX , число степеней свободы уменьшается, k =n-1.

i=1

333

Z – с.в., распределенная по закону N (0,1) , а V – независимая

от Z

с.в., распределенная по закону c2 с k степенями свободы.

t – распре-

Величина

деление

t =

c 2

Стьюдента

распределена по закону, называемому t – распределением

Стьюдента с k степенями свободы.

Если независимые с.в. U и V распределены по закону c2 с k и

F – распре-

k2 степенями свободы соответственно, то величина

æU

деление

Фишера –

F = æV

Снедекора

распределена по закону, называемому распределением Фишера

– Снедекора со степенями свободы k1 и k2 .

Закон распределения функции от одной случайной величины

Если дискретная с.в. X имеет ряд распределения

X	x1	x2	x3	…
P	p1	p2	p3	…

и задана монотонная функция y = g (x ), то дискретная с.в. Y = g (X ), яв-

ляющаяся функцией X , имеет ряд распределения

Y	g (x1 )	g (x2 )	g (x3 )	…
P	p1	p2	p3	…

Если y = g (x ) – немонотонная функция, то среди ее значений g (x1 ), g (x2 ), g (x3 ), … могут быть равные. В этом случае столбцы с равными значениями g (xi ) объединяют в один столбец, а соответствующие вероятности складыва-

ют.

334

Пусть непрерывная с.в. X имеет плотность распределения fX (x); если функ-

ция y = g (x ) монотонна, то с.в. Y = g (X )					имеет плотность распределения
f	Y	(y )= f	X (	g-1 (y )	×	(	g-1	(y )¢	,

				)				)
где x = g -1 ( y ) – функция, обратная к y = g (x ).
В случае, если y = g (x )		немонотонна, для нахождения							fY (y ) область опре-

деления y = g (x ) нужно разбить на промежутки монотонности, на каждом участке найти обратную функцию, найти вклад в плотность вероятности

fY (y ) от каждого участка и результаты сложить:

(y )=

X (

-1 ( y ) ×

(

-1 (y )¢

)

i=1

Двумерные случайные величины

Пусть на одном и том же пространстве элементарных событий W = {w} зада-

ны случайные величины X (w) и Y (w), то говорят, что задана двумерная

случайная величина (X (w),Y (w)), или случайный вектор Z(w) =(X(w),Y(w)).

Геометрическая интерпретация двумерной с.в. – это случайная точка на плос-

uuuur

кости с координатами (X ,Y ), или случайный вектор OM .

Функция распределения двумерной с.в. (X ,Y ) определяется соотношением

F ( x, y) = P{X < x,Y < y} и геометрически определяет вероятность попадания случайной точки (X ,Y ) в бесконечный квадрант с вершиной в точке

(x, y ), лежащий левее и ниже ее.

Закон распределения дискретной двумерной с.в. может быть задан с помощью таблицы

xi	yi	y1	y2	…	ys
		y1	y2	…	ys

x1		p11	p12	…	p1s
x2		p21	p22	…	p2s
…		…	…	…	…
xk		pk1	pk 2	…	pks

где pij = P{X = xi ,Y = y j } – вероятность того, что случайная величина X

примет значение xi , а случайная величина Y – значение y j , pij ³ 0 , при этом

åå pij = 1.

i j

335

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.09.201985.5 Кб2Форма задания1.doc
#
13.03.20161.16 Mб12Формальные языки и автоматы ДКА и НКА.pdf
#
13.03.2016290.58 Кб7Формальные языки и автоматы.pdf
#
19.09.2019198.14 Кб5Формирование корпоративной культуры.doc
#
23.02.2015156.83 Кб7Формулы МС.pdf
#
23.02.2015212.86 Кб6Формулы ТВ.pdf
#
18.11.2019128.37 Кб0Формы настоящего времени.docx
#
23.02.2015301.39 Кб20Фосфор, мышьяк, сурьма.pdf
#
20.09.201990.91 Кб6фосфорная кислота.docx
#
23.12.2018136.04 Кб15фпе.docx
#
22.02.201599.84 Кб10ФПНиТ_Лекция_18.doc