
Формулы МС
.pdf
ФОРМУЛЫ
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Основные понятия
Генеральная совокупность – исходное множество объектов, из которого производится выборка.
Выборкой или выборочной совокупностью называют совокупность объектов, случайно отобранных из генеральной совокупности.
Объем совокупности (выборочной или генеральной) – число элементов данного множества.
X – изучаемый признак (случайная величина); xi – значение изучаемого признака (варианта);
Ni – частота варианты xi в генеральной совокупности;
ni – частота варианты xi в выборке;
k – число различных вариант в выборке (или в генеральной совокупности);
k
N = åNi – объем генеральной совокупности (число элементов);
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n = åni |
– объем выборки; |
|||||||||||||||||||||||
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
p = |
|
Ni |
|
|
|
– относительная частота варианты x в генеральной совокупности |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
i |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|||
|
|
|
|
|
|
|
|
|
|
(вероятность появления значения признака xi ); |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
w = |
ni |
|
– относительная частота варианты x в выборке. |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
i |
|
|
|
|
|
n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числовые характеристики генеральной совокупности |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|||
|
|
x |
Г |
= |
|
åNi × xi = åpi × xi = M (X )– генеральное среднее. |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
N i=1 |
|
|
i=1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
k |
|
|
|
|
|
|
k |
||||||
|
DГ |
= |
|
|
åNi ×(xi - |
x |
Г )2 = å pi ×(xi - |
x |
Г )2 – генеральная дисперсия. |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
N i=1 |
|
|
|
|
|
|
i =1 |
|||||||||
|
sГ |
= |
|
|
|
|
|
|
– генеральное среднее квадратическое отклонение. |
||||||||||||||||
|
|
|
DГ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статистические распределения выборки |
|||||||
|
|
||||||||||||||||||||||||
|
Дискретный статистический ряд ( x1 < x2 < ... < xk ). |
||||||||||||||||||||||||
|
|
X |
|
|
|
x1 |
|
|
|
x2 |
|
… |
xi |
|
… |
xk |
|
||||||||
|
|
ni |
|
|
|
n1 |
|
|
|
n2 |
|
… |
ni |
|
… |
nk |
|
||||||||
205

Интервальный статистический ряд.
Если число значений случайной величины X велико, или случайная величина является непрерывной и может принять любое значение из некоторого промежутка, строят интервальный статистический ряд. Значения вариант группируют по промежуткам (обычно одинаковой длины), в первой строке указывается промежуток, во второй – число наблюдений, попавших в данный промежуток. Для определения оптимальной длины частичного промежутка можно использовать формулу Стерджеса. Пусть значения случайной величины X располагаются на отрезке [a,b] , объем выборки – n . Длина частичного интер-
вала D= |
b-a |
|
, число интервалов k =1 + log2 n (берется ближайшее к log2 n це- |
|||||||||||
|
|
|
||||||||||||
|
1+log2 n |
|
|
|
|
|
|
|
D |
|
||||
лое), первый интервал начинается в точке x =a - |
. |
|||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
min |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
D= xi+1 -xi |
|
D1 |
D2 |
… |
Di |
… |
Dk |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
ni |
|
n1 |
n2 |
… |
ni |
… |
nk |
|
|
|
|
|||
При переходе от интервального ряда к дискретному в качестве xi выбираются середины соответствующих интервалов.
Числовые характеристики выборки
|
|
|
|
|
|
1 |
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|||
|
x |
B |
|
= |
|
åni × xi |
= åwi |
× xi – выборочное среднее; |
|||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
n i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
||||
DB |
= |
å(X i - |
|
)2 |
– выборочная дисперсия; |
||||||||||||||||||
X B |
|||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
|
|
|||||||
sB = |
|
|
|
|
– выборочное среднее квадратичное отклонение; |
||||||||||||||||||
|
DB |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
1 |
|
n |
|
|
|
|
||||
s2 |
= |
|
|
|
DB = |
|
å(X i - |
|
)2 |
– исправленная выборочная дисперсия; |
|||||||||||||
|
|
|
|
X B |
|||||||||||||||||||
|
n -1 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
n -1 i =1 |
|
|||||||||||||
s = 
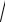 s2 – исправленное выборочное среднее квадратическое отклонение.
s2 – исправленное выборочное среднее квадратическое отклонение.
Оценки параметров генеральной совокупности по выборке
|
M [X ] » |
x |
B – оценка математического ожидания; |
|||||||
Точечные |
D [X |
]» s2 = |
|
n |
|
|
D – оценка дисперсии; |
|||
|
|
|
|
|
||||||
|
|
|
|
n -1 |
B |
|||||
оценки |
s [X |
]» s = |
|
|||||||
|
s2 |
|
– оценка среднего квадратического откло- |
|||||||
|
|
|||||||||
|
нения. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
206
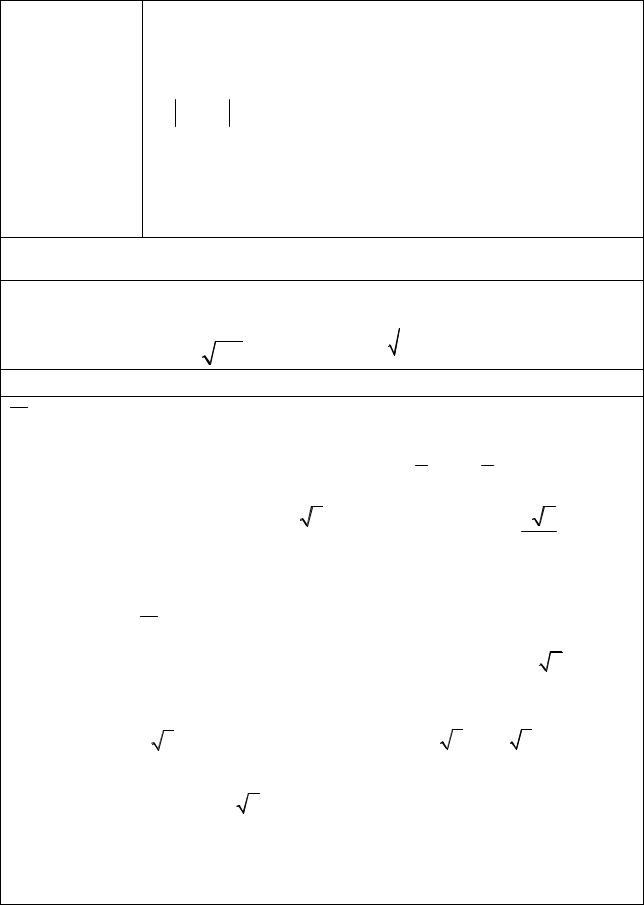
Доверительный интервал (Q* - e ,Q* + e ) заключает в себе
(покрывает) неизвестный параметр Q с вероятностью g ,
Интервальные P (Q - Q* < e )= g = 1 -a .
оценки
Q* – точечная оценка параметра Q; e – точность оценки;
g = 1 -a – доверительная вероятность (надежность) оценки; a – уровень значимости (обычно 0,1; 0,05; 0,01; 0,001).
Интервальные оценки для параметров нормально распределенной генеральной совокупности
Случайная величина Х генеральной совокупности распределена по нормаль-
|
f ( x ) = |
|
1 |
|
e |
-( x -a )2 |
|||||||
|
|
|
|
2s 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
ному закону |
|
|
|
, где s = D[Х ] , a = M [Х ] = X . |
|||||||||
|
|
|
|
|
|
||||||||
s |
|
2p |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Интервальная оценка математического ожидания при известном s
xB – точечная оценка математического ожидания a генеральной совокупности.
1) По заданным n, e и s найти надежность g , g =P(xB -e <a<xB +e).
|
( |
|
|
|
|
|
) |
æ |
e |
ö |
æ e |
|
|
ö |
|
||||
|
|
|
|
|
|
|
n |
= 2Ф (t )= g , |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
P |
|
|
Х в - a |
< e |
= 2Ф ç |
|
|
|
÷ |
= 2Ф ç |
|
|
|
÷ |
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
çs (xв |
÷) |
è |
|
s |
ø |
|
|||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
функция Лапласа, значения находятся по таблицам. Зная s, e и n, можно найти по таблице значений ность g оценки xB математического ожидания a.
где t = e n , Ф(t) – s
функции Лапласа надеж-
2) По заданным n, g |
и s найти точность e . По g определяют t = |
e |
n |
, точ- |
|||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
ts |
|
|
æ |
|
|
ts |
|
|
|
|
ts |
ö |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
ность оценки e = |
|
|
|
, доверительный интервал |
ç xB |
- |
|
|
|
,xB |
+ |
|
|
|
|
÷ . |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n |
|
|
n |
|
n |
|
||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
ø |
|
|||||
3) По заданным s, e и g найти объем выборки n. Из уравнения 2Ф (t ) = g по g
находится t |
, а затем из t = |
e n |
находится минимальный объем выборки |
|||||
|
||||||||
|
|
|
|
|
|
s |
||
éæ ts ö2 ù |
|
|
|
|||||
n = êç |
|
÷ |
ú +1, где [...] – целая часть числа. |
|||||
e |
||||||||
ê |
è |
ø |
ú |
|
|
|
||
ë |
|
|
|
û |
|
|
|
|
207

Интервальная оценка математического ожидания при неизвестном s
Используется распределение Стьюдента t = |
xв |
- |
a |
|
с числом степеней свобо- |
sв / |
|
|
|
||
|
|
n |
|||
ды n = n -1. По заданным n и g можно найти tg , доверительный интервал:
Х -g tg sв < a < Х + g tg sв . При n > 30 можно пользоваться вместо распределе-
 n
n  n
n
ния Стьюдента стандартным нормальным распределением.
Доверительные интервалы для оценки СКО
Требуется оценить неизвестное генеральное СКО s по исправленному выборочному СКО s . Точечной оценкой s является s .
Интервальная оценка s , – доверительный интервал, покрывающий параметр s с заданной надежностью g .
При n £ |
30 |
: |
s2 |
(n -1) |
< s 2 |
< |
s2 |
(n -1) |
, |
c2 – распределение |
c2 (Пирсона) с |
|
|
c2 |
c2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a 2 |
|
|
|
1-a 2 |
|
|
|
n = n -1 степенями свободы, значения находятся по таблицам.
При n > 30: s2 (1 - q)2 £ s 2 £ s2 (1 + q)2 , q = q (n,g ) находится по таблицам.
СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ
Статистические гипотезы утверждают что-либо о статистически устойчивых событиях. Как правило, речь идет о виде функции распределения случайной величины или о параметрах, характеризующих эту функцию распределения.
Основные понятия
H0 – основная (нулевая) гипотеза;
H1 – альтернативная (конкурирующая) гипотеза;
Q– критерий для проверки гипотезы, (случайная величина, служащая для выбора между гипотезами H 0 и H1 );
QB – наблюдаемое значение критерия, вычисленное по выборке;
n – число степеней свободы критерия – число независимых переменных, остающихся после наложения условий на систему случайных величин.
D– область принятия гипотезы (допустимая область) – множество значений критерия, при которых основная гипотеза H0 не отклоняется;
W – критическая область – множество значений критерия, при которых основная гипотеза H0 отклоняется (и принимается гипотеза H1 ).
QK – критическое значение критерия, разделяющее области D и W .
a – уровень значимости критерия, a = P (H1 H0 ), вероятность отклонения
верной нулевой гипотезы (ошибка первого рода) (обычно 0,1; 0,05; 0,01; 0,001).
208

b = P (H0 H1 ) – вероятность принятия неверной нулевой гипотезы,
(ошибка второго рода);
1 - b – мощность критерия, вероятность отклонения неверной нулевой гипотезы (т.е., мощность критерия – вероятность недопущения ошибки
второго рода).
n – число степеней свободы критерия – число независимых переменных,
остающихся после наложения условий на систему случайных величин.
Виды критических областей
Пусть проверяется гипотеза о равенстве генерального среднего xГ данному числу a и для проверки гипотезы используется критерий Q.
Нулевая гипотеза H0 : xГ = a .
Альтернативная гипотеза H1 xГ < a : выбирается левосторонняя крити-
1ческая область из условия Q < Q1 . Задав уровень значимости a, из уравнения P (Q < Q1 ) = a находят левостороннюю критическую точку Q1 .
Альтернативная гипотеза H1 xГ > a : выбирается правосторонняя кри-
тическая область из условия Q > Q2 . Задав уровень значимости a, из
2
уравнения P (Q > Q2 ) = a находят правостороннюю критическую точку
|
Q2 . |
|
|
|
|
|
|
|
|
|
Альтернативная гипотеза H1 |
x |
Г ¹ a : строится двусторонняя критиче- |
||||||
3 |
ская область (обычно симметричная), определяя Q1 и Q2 из уравнений |
||||||||
P (Q < Q ) = |
a |
и P (Q > Q |
|
) = |
a |
|
|||
|
|
. |
|||||||
|
|
2 |
|
||||||
|
1 |
2 |
|
2 |
|
||||
|
|
|
|
|
|||||
Методика проверки гипотез
1.Формулируются основная H0 и альтернативная H1 гипотезы, уровень значимости a и статистической критерий Q.
2.Формулируется правило проверки, определяется соответствующий объем выборки n по заданным уровню значимостиa и мощности критерия 1 – b или из условия минимизации b при данных a и n.
3.Вычисляется QB по результатам выборки.
4.По заданным a и n , по таблицам критических точек распределения критерия вычисляются критические точки QK и строятся D и W .
5.Если QB Î D – основная гипотеза H0 не отвергается,
если QB ÎW – гипотеза H0 отвергается (и принимается гипотеза H1 ).
209

Проверка гипотезы о виде закона распределения с помощью критерия согласия Пирсона c2
X– изучаемый признак (случайная величина).
1.H0 – закон распределения имеет данный вид (например, равномерный,
нормальный и др.);
H1 – альтернативная гипотеза;
a – уровень значимости критерия,
Q = c2 – критерий c2 для проверки гипотезы.
3.Пусть выборка представляется интервальным статистическим рядом. n – объем выборки;
q – количество интервалов, на которые разбит диапазон наблюдавшихся значений величины Х
q
ni - количество экспериментальных данных в i - м интервале, å ni = n .
i =1
pi = P (xi < X < xi +1 ) – теоретическая вероятность попадания варианты в соответствующий интервал.
интервалы |
(x1 ...x2 ) |
|
|
(x2 ...x3 ) |
|
… |
|
(xq ...xq+1 ) |
||
w = n n |
w |
|
|
w |
|
… |
|
wq |
||
i |
i |
1 |
|
|
|
2 |
|
|
|
|
Составляем cнабл2 = å n |
(wi |
- pi )2 = å(ni |
- npi ) |
2 |
||||||
. |
||||||||||
|
|
q |
|
|
q |
|
|
|
||
|
|
|
|
|
|
npi |
|
|||
|
|
i=1 |
pi |
|
|
i=1 |
|
|||
4.По таблице критических точек распределенияc2 находим критическое значение c2 кр = c 2 (a ,n ), где n = q -1- k – число степеней свободы, k – число параметров генерального распределения, оцениваемых на основании наблюденных данных. Если проверяется согласие выборочного распределения с распределением Пуассона, n = q - 2 , если проверяется согласие с нормальным распределением, n = q - 3 и т.д.
5.При полном совпадении теоретического и экспериментального распреде-
лений c2 = 0 , в противном случае c2 > 0 . Задавшись уровнем значимости a , находим табличное критическое значение ca2 , при cнабл2 < ca2 принима-
ем гипотезу H0 , при cнабл2 ³ ca2 отклоняем гипотезу H0 о виде распределения.
В связи с асимптотическим характером закона Пирсона c2 должны выполняться следующие условия:
1)выборка должна образовываться в результате случайного отбора;
2)объем выборки n должен быть достаточно большим
(практически не менее 50 единиц);
3) численность каждой группы должна быть не менее 5 (если это условие не выполняется, производится объединение соседних малочисленных интервалов).
210

ОСНОВЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА
Пусть генеральная совокупность имеет два случайных признака, X и Y . Если изменение X приводит к изменению среднего значения Y , связь меж-
ду X и Y называется корреляционной.
Корреляционный анализ – исследование наличия взаимосвязей между случайными величинами.
Пусть в результате эксперимента для системы( X ,Y ) получена выборка зна-
чений (xi , yi ), i = 1,2,...,n . Если значения xi и yi повторяются, то их группируют:
|
|
|
|
|
|
|
(xi , y j ,nij ), i =1,2,...,l; j =1,2,...,k; |
ånij = n . |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i , j |
|
|
|
|
|
|
|
|
|
|
|
Здесь xi |
и y j |
– наблюдаемые значения X и Y , а nij – частота появления пары |
|||||||||||||||||||||||||||||
значений (xi , y j ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Чаще всего в этом случае данные организуют в видекорреляционной |
||||||||||||||||||||||||||||||
таблицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
|
|
|
|
|
y1 |
|
|
y2 |
|
… |
|
|
yk |
|
|
|
|
|
nx |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
n11 |
|
|
n12 |
|
… |
n1k |
|
|
|
n1 = ån1 j |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x2 |
|
|
|
|
|
|
n21 |
|
|
n22 |
|
… |
n2k |
|
|
|
n2 = ån2 j |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
|
… |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
|||||
xl |
|
|
|
|
|
|
nl1 |
|
|
nl 2 |
|
… |
nlk |
|
|
|
nl = ånlj |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
my |
|
|
|
m1 = åni1 |
|
m2 = åni2 |
… |
mk = ånik |
|
n = åni = åm j |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
i |
|
|
|
i |
|
j |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Группировка данных по значениям xi |
или y j : |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
k |
|
|
i |
|
|
|
|
( x |
l |
|
|
|
j |
|
|
|
|
|
|
( |
|
y |
|
l |
|
k |
|
|
|
||
å ij |
= |
|
|
= |
|
|
) å ij |
= m |
; j =1,2,...,k; |
m |
|
)å i |
= |
å j |
= |
|
|||||||||||||||
n |
n ; i |
1,2,...,l; |
n |
; |
n |
|
|
|
; |
n |
|
|
m |
n , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
j=1 |
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
j =1 |
|
|
|
|
дает законы распределения составляющих(последняя строка и последний |
|||||||||||||||||||||||||||||||
столбец таблицы) и их средние по выборке |
|
B и |
|
B : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
X |
Y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
X |
x1 |
x2 |
… |
xl |
nx |
n1 |
n2 |
… |
nl |
Y |
y1 |
y2 |
… |
yk |
my |
m1 |
m2 |
… |
mk |
средние по выборке xB и yB :
211
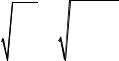
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
åni xi |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
= |
1 |
|
|
åmj y j , |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
x |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
||||||||||||||
выборочные дисперсии компонент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
s X2 = |
1 |
åni (xi - |
|
|
|
B )2 |
|
|
|
|
|
|
|
sY2 = |
åm j (y j - |
|
B )2 , |
|
|||||||||||||||||||||||||||||||||||||||||||
|
X |
|
|
|
|
|
Y |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
исправленные выборочные дисперсии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
sX2 = |
1 |
|
|
|
|
åni (xi - |
|
B )2 |
|
|
|
|
|
|
|
|
|
sY2 = |
|
|
|
|
åm j (y j - |
|
|
|
B )2 . |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
|
Y |
||||||||||||||||||||||||||||||||||||||||||||||||||||
n - |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n -1 |
j |
|
|
|
|
|
|
|
|
||||||||||||||||
Условное математическое ожидание M (Y |
|
|
|
X = x) = mY |
|
x и |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
условная дисперсия D (Y |
|
X = x ) = sY2 |
|
x |
вычисляются при X = x . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Корреляционной зависимостью Y от X называется функциональная зави- |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
симость M (Y |
|
X = x) = f (x). Функция |
f (x ) называется функцией регрес- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сии Y на X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично определяются M (X |
|
Y = y ) = mX |
|
y , D (X |
|
Y = y) = s X2 |
|
|
y |
|
и g ( y ) – |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функция регрессии X на Y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Дисперсия компоненты Y может быть разбита на два слагаемых, |
sy2 =s2f + |
|
2y , |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
s |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
где s 2f = D ( f (X ) = M (( f (X )- my )2 ), |
|
2y = M ((Y - f (X )2 ). |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
s |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
В качестве характеристики связи между X и Y принимается отношение |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 2f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
= |
|
= 1 - |
s |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
YX |
|
s 2 |
s 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
называемое корреляционным отношением переменного Y по переменному |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
X . Аналогично определяется и корреляционное отношение I XY2 |
переменного |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
X по переменному Y . Для выяснения степени тесноты связи необходимо |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рассматривать оба корреляционных отношения, I XY2 и IYX2 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Из определения следует, что 0 £ IYX2 |
|
£ 1. Если IYX2 |
= 1, т.е., |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2y = M ((Y - f (X )2 )= 0 , это означает, что X и Y связаны функциональной |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
s |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
зависимостью, Y = f (X ), если IYX2 |
= 0 , линия регрессии – горизонтальная |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
прямая, изменение с.в. |
X не меняет математического ожидания с.в. Y (в ча- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
стности, это может быть, если X и Y независимы). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ранее при рассмотрении систем случайных величин вводился коэффициент |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
корреляции |
|
|
|
|
|
|
|
|
|
|
|
|
|
M ((X - mx )(Y - my )) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
XY |
|
|
|
|
|
|
|
|
|
s xs y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Для системы нормально распределенных величин X и Y |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
I 2 |
= I 2 |
= r2 . |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
XY |
|
YX |
|
XY |
|
|
|
|
|
В общем случае показатели I 2 |
|
и r2 |
|
связаны неравенствами: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
XY |
XY |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 £ r2 |
£ I |
2 |
£ 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
XY |
|
XY |
|
|
|
|
|
|
При этом возможны следующие варианты: |
|
|
|||||||||||||||
а) |
|
r2 |
|
= 0 , если Y и X независимы, но обратное (в общем случае) неверно; |
|
||||||||||||||
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
r2 |
|
= I 2 |
|
=1 тогда и только тогда, когда имеется строгая линейная функ- |
|
||||||||||||
|
|
XY |
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
циональная зависимость Y от X ; |
|
|
|
|
|
||||||||||||
в) |
|
r2 |
|
£ I 2 |
=1 |
тогда |
и только |
тогда, когда имеется строгая нелинейная |
|
||||||||||
|
|
XY |
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функциональная зависимость Y от X ; |
|
|
|
||||||||||||||
г) |
|
r2 |
|
= I 2 |
|
< 1 тогда и только тогда, когда регрессия Y по X строго линей- |
|
||||||||||||
|
|
XY |
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на, но нет функциональной зависимости; |
|
|
|
||||||||||||||
д) |
|
r2 |
|
< I 2 |
|
<1 указывает на то, что нет строгой функциональной зависимо- |
|
||||||||||||
|
|
XY |
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти, а некоторая нелинейная кривая регрессии приближает зависимость |
|
||||||||||||||||
|
|
лучше, чем любая прямая линия. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Итак, в качестве показателя стохастической связи между двумя случайными |
|
||||||||||||||||||
количественными переменными X |
и Y |
следует выбрать корреляционное от- |
|
||||||||||||||||
ношение I XY2 |
(или IYX2 ), если закон распределения системы ( X ,Y ) |
неизвестен; |
|
||||||||||||||||
если |
|
есть основания считать, что |
система ( X ,Y ) имеет нормальный закон |
|
|||||||||||||||
распределения, то вместо корреляционного отношения следует использовать |
|
||||||||||||||||||
коэффициент корреляции rXY . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Свойства коэффициента корреляции |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1°. |
|
rXY |
|
£ 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2°. |
Для независимых с.в. rXY = 0 . |
|
|
|
|
|
|
|
|||||||||||
3°. |
Если с.в. X |
и Y |
связаны |
линейной |
функциональной |
зависимостью, |
|
||||||||||||
|
Y = aX + b, a ¹ 0 , то |
|
rXY |
|
= 1, |
причем rXY |
= 1 при a > 0 и rXY = -1 при |
|
|||||||||||
|
|
|
|
||||||||||||||||
|
a < 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4°. |
Если |
rXY |
|
= 1, то с.в. |
X и Y связаны линейной функциональной зависи- |
|
|||||||||||||
|
мостью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
213
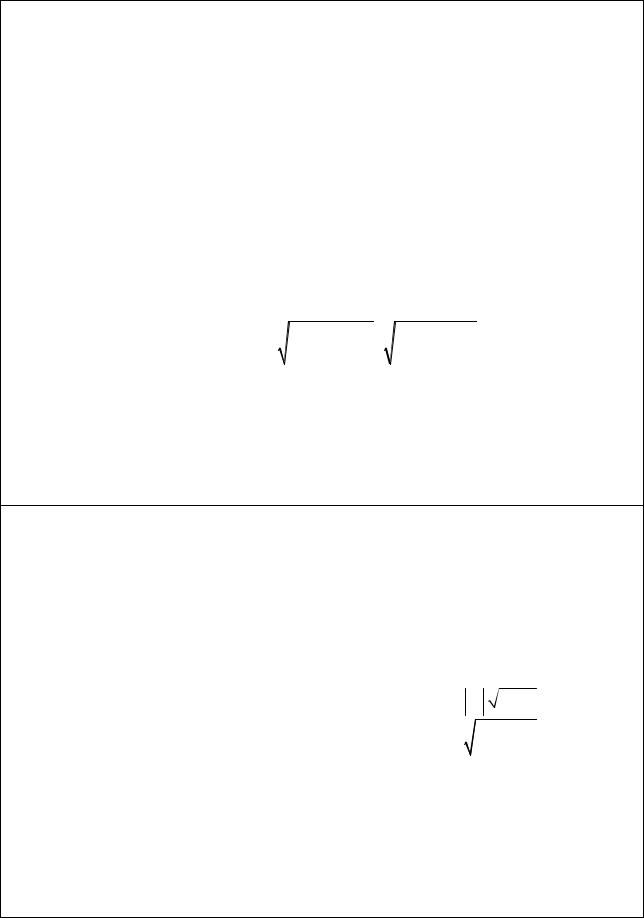
Коэффициент корреляции rXY |
|
|
является мерой линейной связи между случай- |
|||||||||||||||||||||||||||||||||||||
ными величинами: если |
rXY = 0 , |
с.в. |
независимы, |
|
|
если |
|
rXY |
|
= 1, с.в. связаны |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
линейной зависимостью, при |
|
rXY |
|
¹ 1 зависимость носит иной характер. |
Чем |
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
больше |
|
rXY |
|
, тем больше |
связь |
|
между X |
и Y |
похожа |
|
на линейную. |
При |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
rXY > 0 говорят о положительной корреляции между X |
|
и Y , при rXY < 0 – |
||||||||||||||||||||||||||||||||||||||
об отрицательной корреляции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
В качестве точечной оценки коэффициента корреляции rXY |
|
берут его выбо- |
||||||||||||||||||||||||||||||||||||||
рочное значение r* : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
XY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å(xi - |
|
|
)(yi - |
|
) |
|
|
|
|
|
|
|
||||||||||||
Для несгруппирован- |
|
* |
|
* |
|
|
|
|
|
|
X |
Y |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ных данных |
|
rXY |
= r |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
å |
(xi - X )2 |
|
× å(yi - Y )2 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
åånij xi y j - n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Для сгруппированных |
|
|
|
|
|
|
|
|
X |
Y |
|
|
|
|
|
|||||||||||||||||||||||||
данных |
|
rXY* |
= r* = |
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
nsX sY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интервальная оценка коэффициента корреляции и проверка значимости
1.H0 : rXY = 0 (отличие rXY от нуля статистически недостоверно); H1 : rXY ¹ 0 (отличие rXY от нуля статистически значимо).
2.Выбирается уровень значимости a .
3.Статистический критерий – t-критерий Стьюдента с n - 2 степенями свободы.
4.По результатам выборки вычисляются r* – точечная оценка коэффициен-
r* 
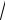 n - 2
n - 2
та корреляции и выборочное значение критерия tB =  .
.
1- (r* 2)
5.Находится tkp = t (a, n - 2) по таблицам критических точек распределения Стьюдента
6.D , область принятия гипотезы H0 : tB < tkp ,
W , критическая область (область принятия гипотезы H1 ): tB > tkp .
214
