1. Изучение свободных и вынужденных колебаний
.pdf
При вынужденных колебаниях в контуре кроме рассмотренного нами резонанса напряжения на конденсаторе и резонанса тока имеет место резонанс и других изменяющихся со временем величин q(t), εL(t),UR(t). Но все эти явления резонанса, происходящие в последовательном контуре, т.е. когда источник напряжения и все элементы контура соединены последовательно, называются резонансом напряжений, в отличие от случаев, когда источник эдс подключается к контуру параллельно. В этих случаях наблюдается резонанс токов, который в данной работе не рассматривается.
1.1.4. Определение добротности контура при вынужденных колебаниях.
Добротность при вынужденных колебаниях определяет амплитуду напряжения на конденсаторе в резонансе. Действительно, из (49) имеем:
.
При не очень большом сопротивлении, полагая |
и |
учитывая (32), преобразуем выражение (55)
или
Т.е. добротность колебательного контура показывает, во сколько раз резонансная амплитуда напряжения на конденсаторе больше амплитуды вынуждающей эдс. Аналогично можно определить амплитуду напряжения на индуктивности L
Таким образом, амплитудные значения UoL и Uoc при резонансе равны по величине, но согласно (47) находятся в противофазах, поэтому их суммарное значение равно нулю. Отсюда и название –резонанс напряжений. При резонансе величина тока определяется лишь падением напряжения на активном сопротивлении, т.е. как и следовало ожидать согласно (53).
Добротность характеризует также и ширину резонансной кривой, или полосы пропускания, данного контура. Это чрезвычайно важно для настройки контура на определенную частоту.
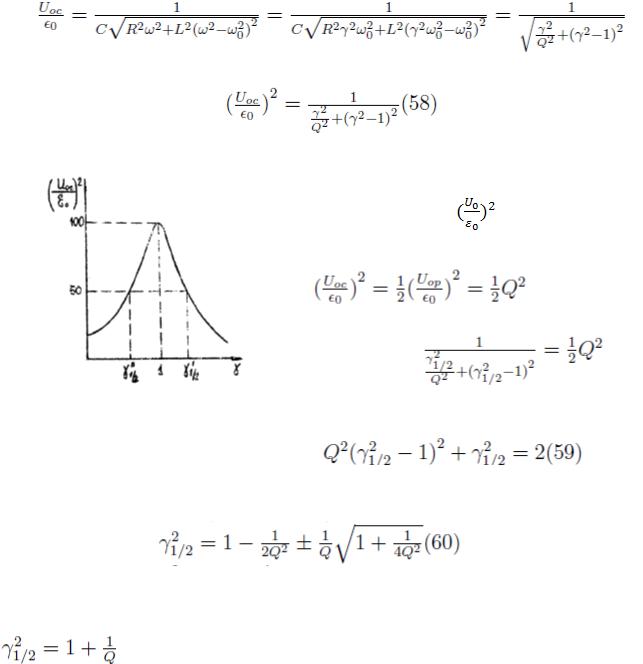
Чтобы это показать, построим резонансную кривую Uc=f(ω) в безразмерных координатах. По ординате отложим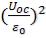 
, а по абсциссе
отношение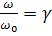 
(рис.7). Из (49), используя (5) и (32), найдем
или
где Q –добротность контура (32).
Если теперь найти значение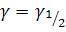 
, при
котором величина |
вдвое меньше |
резонансной величины, т.е. |
|
Рис.7. Резонансная кривая в относительных координатах.
то выражение (58) можно записать
или
.
Решая уравнение (59), находим, что
Рассмотрим контуры с большой добротностью (Q>>1), членами порядка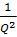 
можно пренебречь, и из (60) получим
или
.
Из (61) видно, что существуют два значения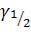 
, расположенные по обе стороны максимума резонансной кривой 
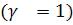, при которых величина
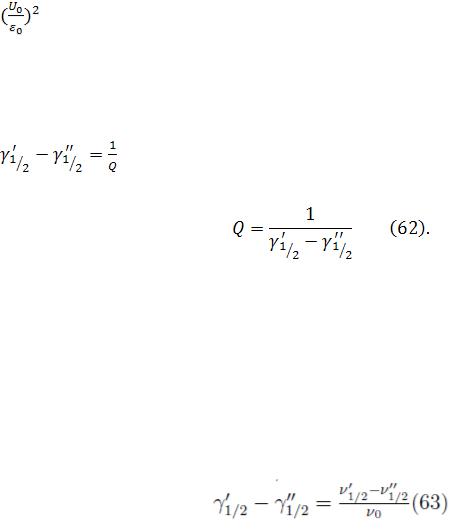
в два раза меньше своего максимального значения. Обозначив эти
значения через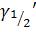 
и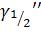 
, из (57) имеем
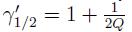и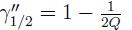 
, отсюда
или
Разность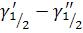 
называют полосой пропускания или полушириной
резонансной кривой. Чем выше добротность контура, тем меньше полоса пропускания, тем лучше избирательность контура.
Примечание. Полуширину резонансной кривой можно рассчитать и из зависимости Uc(ν). Для этого нужно провести горизонтальную линию на
уровне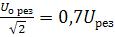 
и спроецировать точки пересечения на ось ν. Тем самым мы получим 
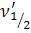и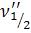 
. Т.е.