
шпоры добродей
.docx|
37.Понятие субоптимальных решений, методы построения субоптимальных решений. Субоптимальное решение – близко к оптимальному по существенным для выбора решения показателям. 1)Выпуск важнейших видов продукции 2)Расход важнейших ресурсов 3)По функции цели 4)По структуре выпуска S(X) – множество субоптимальных решений Выбор из субоптимальных решений должен осуществляться на основе дополнительных характеристик. Единого метода для построения субоптимального множества не существует, но его можно получить с помощью вариантных расчетов. (можно менять в малых диапазонах ресурсы, цены, коэффициенты , структуру продажи.) В прикладных системах обычно предусмотрено построение некоторых видов субоптимальных решений (в пределах Е) 59 Методы решения задач с двумя критериями (на примере выбора структуры портфеля ценных бумаг). Vi-ожидаемая доходность итой ЦБ, Vi=Vo+βi(Vp-Vo), Vo-доходность безрисковых ЦБ, βi-бета рейтинг (индекс доходности данной бумаги относительно среднего индекса на рынке) Vp – средняя рыночная доходность рисковых бумаг. Портфель должен быть диверсифицирован. Ri риск ЦБ. В качестве риска можно взять дисперсию доход за предшеств период. Vп →max, Rп→min. Шар, Марковец первые предложили методы формирования эффективного портфеля. 1. max Vп при Rп≤Rcp (макс риска котор вправе доп-ть) 2. зеркальный подход: min Rп, Vп≥Vср. Оба подхода могут дать эквив рез-ты. Vi=Vo+βi(Vp-Vo), βп линейно зависит от β рейтинга входящих в него бумаг. Rп = Rдиверс+ Rсист, Rдиверс – минимально, поэтому при расчетах не учитывается. Rсист = Rструктуры+ Rиндивид-х хар-к. 61 Формулировка проблемы выбора решений с учетом типов неопределенностей в информации. Содержательная характеристика типов неопределенностей в задаче. Для исследов проблем в усл неопред-ти необходимы сведения о следующих вопросах: отличие вероятностного задания знач факторов от общего понятия неопределенности; типы возм-х неопред-тей в усл операции. Вследствие влияния неопред факторов каждой стр оперирующей стороны соответствует не ед исход операции, как в детермин случае, а мн-во возм исходов. Конкрет реал-я исхода опред-ся сочетанием реализаций случ параметров (факторов), а также знач-ми фиксиров и управляемых факторов. Относит-но вероятностей возм-х исходов операции в усл неопределённости оперирующая сторона не располагает той инфо, кот имеется относит стох факторов - известных стати-х хар-х. Возможны 2 случая. 1) Вероятность возмо исходов не имеет физич смысла. Примеры таких сит (факторов не стох природы): стр неопред-ти - наличие неск-х оперирующих сторон с неизвестными и несовпадающими целями; концеп-ные неопределенности, связ-е с реш особо сл проблем перспективного хар-ра с неизв последствиями, что обусловлено нечетким представлением оперирующей стороны о своих целях и возм-тях, а также о целях и возможностях др уч-в операции, о буд усл трудностью кол-й оценки сл-х, не формализуемых целей, имеющих только кач-е (содержательное) описание; природные неопределенности как следствие недостаточ изученности оперирующей стороной "природы" - всей совокуп-ти обстоятельств, связ-х с операцией. 2) Вер-ть возм-х исходов имеет физич смысл, но известны оперирующей стороне с недостаточ для их прим-я точностью. Этот случай соответствует ситуациям упр недостаточно изученными стох процессами. Многостор ЗПР делят на конфликтные и кооперативные; в последних цели оперирующих сторон совпадают или не противоречат др др хотя бы частично. В случае полной противоположности целей ЗПР называют антагонистическими. В конфликтных одноуровневые задачах принятия реш оперирующие стороны не связаны отнош в форме подчинения; многоуровневые многосторонние антагонистические задачи возникают в сис-х, им-х иерархическую стр и неск ур-й упр, из кот нижние подчинены верхним, но обладают определёнными правами относит-но принятия с/м-ных реш. Такие задачи в наст время слабо изучены в силу их чрезвычайной сложности. Мат аппарат для ан конфликтных ситуаций в усл многократно повторяющейся операции - теория игр и теория минимакса; теория статистич реш. При рассм ЗПР в усл прир неопределённостей рассматривают 2 ситуации: не представляется возм-тей провед-я экспериментов для уточнения вероятностей возможных исходов операции; проведение экспериментов возможно. В 1-м случае выбор реш осуще-ся на основе спец критериев, разработанных в теории статистич реш. Выбор критерия является здесь концептуальной проблемой - должен учитывать цели и содержание операции, последствия реш. Такие ЗПР наз-ся статистич играми без эксперимента. В случ возм-ти экспер-тов возникает ?, ск-ко и каких экспер-тов целесообразно осущ-ть для уточнения вероятностей возм-х исходов (с учётом затрат рес-в и времени). Ответ на эти вопросы получают с помощью теории план-я экспер-тов. Отличие ЗПР в усл конфликта от др видов ЗПР в условиях неопред-ти: известны цели и набор возм-х управлений др уч-в; все участники активны и разумны. В играх с "природой" этого нет, что усложняет ЗПР и снизить степень неопределённости здесь возможно только за счёт эксперим-в. Наиб сл класс ЗПР - ЗПР в усл неопределённостей концептуального хар-ра. Эти задачи называют ЗПР в усл неопред целей и возмож-тей. Формальный аппарат оказывает здесь незначительный эффект. Реш задачи выливается в чисто концептуальную проблему, в необх-ть снижения неопред-ти относительно концепций - целей и возмож-тей их достижения. Наиболее часто здесь прим-ся процедуры сис ан - экспертные, эвристические, дерева целей, сценариев и т.п.
68 Выбор решений в ситуациях полной неопределенности. Принцип недостаточного основания Лапласа, критерии Вальда и Сэвиджа, их применение, достоинства и недостатки. Критерий Вальда(W) выбор наилучшей ситуации из наихудшей. По строкам ищется мин. A1=minjai, W=max(min aij). Критерий Сэвиджа: Строят матрицу экономического риска R=x r1 r2. Элементы этой матрицы показывают потерю дохода от неудачного выбора стратегии. S=min i(max j rij) 37. Критерий Вальда: Критерий Сэвиджа:
Критерий Гурвица:
36 Коэффициенты прямых материальных затрат, косвенных и полных затрат в модели МОБ. (Плановые) коэффициенты прямых затрат (нормативы затрат; ?удельные затраты) – затраты промежуточной продукции на единицу ВВ в каждой отрасли: (a ij = z ij / X j) - сколько нужно затратить продукции отрасли i, чтобы произвести единицу валовой продукции отрасли j. Коэффициенты a ij составляют матрицу прямых материальных затрат (плановую матрицу) – А , отражающую явные связи 1-го порядка. Ее диагональные коэффициенты отражают внутриотраслевой оборот данной отрасли. Здесь много нулевых коэффициентов. Коэффициенты полных затрат составляют матрицу полных затрат (технологическую матрицу Леонтьева) -- В., которая отражает полные связи отраслей друг с другом : 1, 2, 3, 4, 5 порядка. Коэффициенты полных (материальных) затрат (bij) получаются путем добавления к прямым затратам всех косвенных. (bij = z ij /У j ) -- затраты отрасли i , необходимые для производства единицы конечной продукции отрасли j В = (Е – А)-1 Х= АХ+У=ВУ В среднем по народному хозяйству коэффициенты полных материальных затрат превосходят коэффициенты прямых материальных затрат в 1,5 - 2 раза. Пример: Затраты электроэнергии на производство кабельных изделий (руб.руб.)(1975): прямые – 0.012 полные – 0.078 40 Развитие модели МОБ для учета динамики процессов, ограниченности ресурсов, изменения приоритетов развития экономических подсистем. Усовершенствование модели МОБ.-теоретически возможно;-детализация иногда лишняя;-управление сальдо ввоза-вывоза(оптимизация);-aij можно взять как функции,- а не фиксировать ср.значениями.
42 Транспортная задача и производственно-транспортные модели, их применение в обосновании территориальных схем развития и размещения производства. Задача о размещении (транспортная задача) – это РЗ, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям. Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции. Закрытый транспортный блок – продукция производится в системе и полностью потребляется. Открытый транспортный блок – продукция еще остается в избытке. Исходные параметры модели ТЗ n – количество пунктов отправления, m – количество пунктов назначения. ai – запас продукции в пункте отправления Ai.(i=1,n). [ед. прод.]. bj – спрос на продукцию в пункте назначения Bj.(j=1,m) [ед. прод.]. cij – тариф (стоимость) перевозки единицы продукции из пункта отправления Ai в пункт назначения Bj [руб./ед. прод.]. Искомые параметры модели ТЗ Поставщики (i=1,…m)-минимизировать затраты на поставку продукции потребителям. Потребители (j=1,…n).Для каждого поставщика известен объем, ктр он может поставить-aij.bij-потребности потребителя . Сij-затраты на поставку единицы объема (транспортные).=>ΣcijXijmin-суммарные затраты на поставку (1й критерий). 1).Баланс
по поставщикам: 2).Баланс
по потребителям:
3).Хij>=0 или αij=<Хij=< βij. Актуальность транспортной задачи для предприятия => можно рассматривать несколько видов взаимозаменяемых или частично взаимозаменяемых грузов (в рамках одной модели). Многоиндексные транспортные задачи => учитывается степень взаимозаменяемости. Этапы построения модели 1. Определение переменных. 2. Проверка сбалансированности задачи. 3. Построение сбалансированной транспортной матрицы. 4. Задание ЦФ. 5. Задание ограничений. ЦФ представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления модели ТЗ является транспортная матрица. Сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, т.е. (2):
Для фиктивных перевозок вводятся фиктивные тарифы cф, величина которых обычно приравнивается к нулю cф =0. Но в некоторых ситуациях величину фиктивного тарифа можно интерпретировать как штраф, которым облагается каждая единица недопоставленной продукции. В этом случае величина cф, может быть любым положительным числом. Задача о назначениях – частный случай ТЗ. В задаче о назначениях количество пунктов отправления равно количеству пунктов назначения. Объемы потребности и предложения в каждом из пунктов назначения и отправления равны 1. Примером типичной задачи о назначениях является распределение работников по различным видам работ, минимизирующее суммарное время выполнения работ. Переменные задачи о назначениях определяются следующим образом
Модель развития и размещ-я пр-ва.
Ф-я
цели
52 Принцип Беллмана, его содержательное истолкование и построение динамической модели в форме реккурентных уравнений. Принцип оптимальности впервые был сформулирован Р. Беллманом в 1953 г. Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование — процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги. Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной будет являться оптимальной траекторией относительно начала и конца. Уравнения Беллмана. Принцип Беллмана – на любом (к-ом) шаге при выборе упр-ии Uk необходимо учитывать не только эффект на данном шаге, но также суммарный эффект на оставшихся шагах.
Всякий отрезок оптимальной траектории – оптимален. Оптимизация многошагового процесса: W(Sn)
– эффективность движения из Sn
в SN
(конечное).
Рассчитывают для каждого состояния,
двигаясь из конечного в начальное.
W(SN)=0,
n=N..0.
Правило носит название уравнения
Беллмана:
Принцип выбора управления. Uk = max[ fk (Ek-1;U) + Zk+1 (Ek)] условно макс эффект оставш шагов. Uk э Dk – это множ-во доп управлений на k шаге; Uk – м выбирать. На произвольном шаге это уравнение решить невозможно, т.к. 2 слагаемое не известно.
Состояние
системы после 1го шага.
Конечная составляющая либо фиксир, либо указана область конечных состояний. Реккурентное
уравнение Беллмана
На последующем шаге уравнение упрощается
54 Схема обратного хода расчетов по модели ДП – содержание этапа условной оптимизации. Уравнение каждого шага связ с соседними уравнениями. Вид функции f1…fn считается известным. Функция зависит от 1го параметра. Примечание: возможные значения пар-ра Еп-1 м определить заранее не решая уравнение. Если определим в виде дискретной сторки, какой-то ряд чисел, то перебирая их мы м получить условные max (~Zn) Когда решим 2е уравнение мы получим суммарный максим эффект п и п-1 шага. Пока не дойдем до 1го шага,. Этот этап наз-ся условной оптимизацией. Решив 1е уровнение мы получим Z1* - суммарный максим эффект с 1 по п шаг. Мы нашли опртим уравнение на U1*. (усл max эффект: ~Zn(En-1) ~Un(En-1); ряды значений ~Zn-1(En-2) ~Un-1(En-2); ~Zn-2(En-3) ~Un-2(En-3); … ~Z1*(E0) ~U1*(E0) ). Множество возможных состояний En-1 к началу последнего шага должно быть заранее предопределено. Решив уравнение для последнего шага мы получим не одно решение, а множество. ~Un - условно максимальное решение для последнего шага. Для n-1 шага:
В
результате решения получится несколько
решений (множество результатов)
I этап условной оптимизации (управление на первом шаге и результат известен) II этап безусловной оптимизации (от 1 шага к конечному, вычисление эф управлений на последующих шагах). Прямое направление Е0 ---E1|-------|Ek-------|Ek+1-------|En-1-------|En U1---------------------->U*n-1 Un* U1*(E0) E1*(E0;U1*) – оптим состояние к коцу 1го шага => опред уранение на 2 шаг U2*(E1*) => U2* E2*(E1*;U2*) => U2* U1*-> E1* -> U2* -> E3* -> U3* ->… -> Un* Отличие метода прямого хода (Ex: модель управления запасами): Е0 E1 Ek Ek-1 En-1 En |-------|---------|----------|------------|------------| ------> I этап: (услов оптимизация): ~Z1*(E0) ~Zn-2(En-3), ~Zn-1(En-2) … ~Zn(En-1) <------- ~U2*(E0) ~Un-2(En-3); ~Un-1(En-2)… ~Un(En-1) II этап: (безуслов оптимизация): ------> U1*-> E1* -> U2* -> E2* -> U3* ->… -> Un*
66 Применение ЭММ для решения проблем совершенствования управления предприятием. Модель распределения единого фонда оплаты труда (ЕФОТ) между подразделениями предприятия. Рассматривается ситуация: Корпорация (1,2,…,9) – подряд, ЕФОТ – дополнительное распределение Для каждого подразделения рассчитывается коэффициент эф-ности =>ЕФОТ распределяется с учетом коэффициентов. Дополнительно учитываются взаимные претензии распределения в финансовой форме (ЕФОТ д.б. распределен с учетом Кэ) 1) Учет взаимных претензий распределения в денежной форме. Показатели результативности по каждому подразделению учитывают специфику их работы. Оценка производится по результатам работы подведомственного распредления. Некоторые руководители оценивают по др. показателям, кот не обязательно выражаются в количественной форме. Речь идет об условно-чистой продукции. Производительность труда – не ЧП. Расходы на содержание аппарата управления. Структура подразделений. Коэффициенты значимости. Показатели по отдельным подразделениям (каждый показатель на коэффициент его значимости):
i – номер подразделения , i = 1,n Пi – относительное изменение показателей Защищенные законодательством статьи оплаты труда обязательно выполняются. Сам коэф-нт непосредственно не используется для распределения ЕФОТ, т.к.: 1) взаимные претензии; 2) необходимо распределение сбалансировать, т.к. ФОТ увеличивается, а показатели эффективности подразделений значительней увеличиваются, их необходимо нормировать с учетом динамики ЕФОТ. Модель нормировки – задача МП (нелинейная). После нормирования учитываются претензии, коэффициенты заново нормируются и подсчитываются доли. На предприятии есть специальная структура, которая учитывает претензии. В отчете 3 в матице корректируются коэффициенты:
К – определяет долю оплаты труда работника в подразделении. Модель - интерактивная, есть модули, кот дают инф-цию, а рук-во ей не следует.
49 Общая схема прогнозных расчетов и ее содержание. Истолкование места и роли отдельных блоков и этапов прогноза. Опред проблем и целей развития сис на основе анализа тек сит и выявл уже возникших противоречий - не самый эф подход.Он обеспечивает (в случае успешного реш проблем) развит по кривой синусоидального типа относит-но лучшего вар траектории и даёт опред потери рес-ов, сниж темпов развития. Более рационален подход, когда управляющие воздействия упреждают перспективные противоречия - это реал-ся введением этапа прогноз-ния буд сит.Прогноз-ние явл формой выр-ки возм реш в виде "конуса", гр с послед-щим усечением и отбором.Осн принципы сис-ти в прогноз-нии, выр-ке и принятии реш: учёт "фона" сис - внеш усл и взаимосвязей; преодоление лок-ых, изолированных подходов к упр-ю; учёт динамики процессов и явл; учёт специфики объектов упр. Посл-й принцип реал-ся на всех этапах выр-ки и принятия реш, однако чаще всего выдел-я спец-й этап анализа объекта упр. Его рез-м д.б. созд надёжной прогност-й модели объекта; экспер-ты с моделью явл осн сред-м получ прогнозной инф-ии. Исп-мые методы опираются на прим теории инф-ции и измер-й, теории подобия, теории вероят-тей и мат статистики, методов экстраполяции и интерполяции, эк ан.Инф-ное обеспеч на этапе ан объекта упр играет важн-ю роль. Сущ-ет класс-я ист-ов инф по её содер-ю и дост-ти (от этого существенным образом зависит выбор методов прогноз-я); инф м.б.:колич-й, кач-й, смеш-й; компетентной, малокомпетентной;однородной, неоднородной;достоверной, вероятностно-достоверной; периодич, непериодич и т.д.Известно много методов прогноз-ия: экстраполяционные, статистич-ие, эксп-е, эврист-е, программные, сценариев и др.
51 Общая формулировка зависимости эффекта управления от параметров экономического процесса. Классификация задач принятия решений. Недостатки однокритериальной задачи выбора решений. Пусть рассматривается некоторая операция - управляемый процесс; эф-ть упр хар-ся критериями F, допускающим кол оценку, причём критерии могут быть заданы и в неявной форме - алгоритмически.Крит зависят от факторов, кот делят на 2 группы:управля-е (контролируемые) факторы; выбор их знач осущ-ся оперирующей стороной в соотв с принятой стр упр;неуправляемые (неконтролируемые) факторы; влиять на их значения оперирующая сторона не может; в состав таких факторов может входить и время на реализацию решений.Среди неконтролируемых факторов также выделяются 3 группы:детермин-е (неслучайные) факторы; их знач известны оперирующей стороне до начала операции;стохастич факторы; это случ-е величины и процессы; законы распред вероятностных хар-тик их известны оперирующей стороне;принятие реш; вып-ние реш и оценка рез-в,неопред факторы; для каждого из них известна лишь область возм знач в момент принятия реш.Критерии выбора реш зависят от перечисленных факторов: F=F(x1,x2,...,xm,a1,a2,...,an,y1,y2,...,ys,z1,z2,...,zr,t) (1) Здесь вектор X=(x1,x2,...,xm) обозначает управляемые факторы; вектор A=(a1,a2,...,an) - дет ф; вектор Y=(y1,y2,...,ys) - стох факторы; вектор Z=(z1,z2,...,zr) - неопред ф.Выбор возм-х знач управляющих факторов (переменных) ограничен в силу ряда естеств причин (дисциплинирующие ограничения); эти условия можно формализовать в виде соотношений:gi=gi(X,A,Y,Z,t) (2) Усл (2) опр-ют допустимые обл возм-х знач контролируемых факторов; аналогичным образом м. б. ограничены и обл знач неконтролируемых факторов в предположении, что эти области известны оперирующей стороне.Цель операции формализуется (приближённо) в виде: найти реш, при кот достиг-ся макс (мин) критериев F.В приведенной постановке отсутствует полная мат строгость, но это не явл недостатком, ибо наличие неопред-стей в усл ЗПР не позволяет реализовать наил выбор альтернатив в форме классической задачи оптимизации. Тем не менее, поиск реш на основе мат расчётов возможен после уточнения понятия "лучшее" реш и такой подход имеет несомненные преим-ва по срав с произвол субъективным их выбором. Класс-я задач:Однокрит,многокрит;статичес,динам;детермин, стох, с неопред усл;лин-е, нелин, целочисл, смешанные;краткосроч, долгосроч;одноуровневые, многоуровневые, многосторонние;кооперативные, конфликтные.Принятие реш в усл стох прир влияющих факторов основыв-ся на испо крит, учитывающих известные законы распред знач этих факторов. Статистич хар-ки - мат ожид, дисперсия и др. прим-ся для опр стр и упр-й, лучших в заранее определённом смысле. Однокрит статич ЗПР в детерм усл-х иссл-ся методами МП. В усл риска прим-ся методы теории вер-тей, теории игр, статистических решений и др., а также экспертные методы.Для задач МП также имеется опред градация по сложности их содержания и применяемых методов: линейные, квадратичные, выпуклые, сепарабельные, нелинейные общего вида. Для задач МП последнего типа применяют (в случае их полиэкстремального характера) методы поиска экстремумов (градиентные, наискорейшего спуска, покоординатной оптимизации, овражные, случайного поиска с адаптацией и т.п.). Недостатком подхода, общим для таких методов, явл возм-ть значит-х отклонений от ожидаемых рез-в в конкрет ед-х операциях; это означает, что полученное реш не гарантирует. 55 Способы нормализации критериев. Понятие ряда приоритета. Жесткая и гибкая схемы учета приоритета критериев. Понятие
ряда приоритета. Жесткая и гибкая
схемы учета приоритета критериев.Нормализация
критериев - сложная концептуальная
проблема, возникает при построении
всех схем компромисса за немногими
исключениями - например, для принципа
относительной уступки.Большинство
способов нормализации основано на
понятии идеального результата
операции, задаваемого вектором
идеальных значений
критериев Eи=(Eи1,Еи2,...,Еик);
вектор Е приводится к безразмерному
виду:Ен=(Ен1,Ен2,...,Енк),
где Eнq=Eq/Eиq,
q=1,...,k Успех решения проблемы зависит
от объективности определения идеального
результата. Способы выбора идеальных
значений критериев:способ 1 - путем
прямого задания идеальных значений Eиq;
недостаток - сложность и субъективность
подхода; способ 2 - в качестве идеальных
берутся максимально возможные значения
частных критериев; недостаток -
нарушение равноправия критериев -
предпочтение автоматически отдается
критерию с наибольшим максимальным
значением; способ 3 - в качестве
идеального принимается максимально
возможный разброс значений
соответствующего критерия: Енq=MAX
Еq-
MIN Eq
Ряд
приоритета представляет собой
упорядоченное множество индексов и
отражает качественные соотношения
критериев по важности, количественно
важность критериев при этом не
оценивается. Применяют два основных
принципа учета приоритета критериев:
1)принцип жесткого учета приоритета;2)принцип
гибкого учета приоритета. Принцип
жесткого учета основан на последовательной
оптимизации в порядке их следования
в ряду приоритета; недостаток - чрезмерно
быстрое сужение области компромисса.
Принцип гибкого приоритета реализуется
через задание весов, причем во многих
ситуациях веса не являются фиксированными
и зависят от текущих значений отдельных
критериев (последний подход реализуется
с помощью специальных процедур).
Рассмотрим схему решения многокритериальной
задачи ЛП с применением принципа
жесткого приоритета; такая схема в
простейшем случае включает следующую
последовательность однотипных шагов:
шаг 1: в соответствии с рядом приоритета
в качестве функции цели задачи ЛП
берется критерий Е1
и решается задача:
шаг
3:
формируется задача с очередным по
важности критерием в качестве функции
цели - Е3
и дополнительными ограничениями на
значение предыдущих критериев:
|
45. (Вопросы надежности долгосрочных прогнозов с применением экономико-математических моделей. Общая характеристика современных подходов в прогнозировании). Опыт применения мат-х методов реш-я эк-х проблем. Сферы применения мат-х методов и множественность соотв-х прикладных дисциплин. Искусство выр-ки лучших реш старо как человечество; наука о выработке альтернатив молода; наука поиска и выбора лучших реш очень молода ей около 50 лет. Теория прин реш (ТПР) развивалась очень интенсивно, но пока ещё нах-тся в стадии становления во многих своих важных разделах.Сущ-ет большое кол-во научных дисциплин, имеющих прямое отнош к проблемам выбора реш: мат программ-ния (МП) и исследование операций (ИС), теория игр, теория статистич реш, теория автоматич-го упр, сист анализ, эк кибернетика и др. Эти дисциплины рассматривают одну и ту же проблему: науч ан возм-х способов дейст-й с целью нахождения такого из них, кот в опред смысле явл наилучшим. Однако они рассматривают объекты разной прир и в различ усл. В этом смысле они явл составляющими общей дисциплины ТПР. Вместе с тем не сущ единого мнения о месте ТПР в общем процессе познания - в зависимости от сфер научной деят-ти и интересов многие спец-ты склонны считать ТПР либо предметом, либо основной составной частью своей научной дисциплины. Тем не менее, более общий х-р общей ТПР в сравнении с МП, ИС, СА, планир-ем и прогноз-ем, другими дисциплинами такой же целевой направленности неоспорим. Проблема принятия реш имеет универсальный и всеобъемлющий х-р - возникает в любой сфере целенапр деят-ти и составляет её принципиальную сущность. Особенно актуальны вопросы выр-ки и принятия реш в сфере упр слож сис. Проц проектирования, разраб-ки, созд-я упр слож сис связаны с необх-тью принимать большое кол-во реш как относит-но сис в целом, так и отд её частей и Эл-в. Т.О, можно сделать вывод: проблема прин-я реш – центр-я в упр объектами любой сложности и особенно сложных. 63 Основные понятия и определения матричной игры. Принципы применения матричных игр для исследования экономических проблем. Принципы применения матричных игр для исследования экономических проблем игра - модель повторяющейся конфликтной операции; м.б. парной или множественной; Правила игры - сис усл, опред-щих возм действия игроков (оперирующих сторон); считается, что они известны для сторон и их соблюдение гарантировано;игроки - стороны, участв в игре; м образовывать коалиции;оценка резу-в игры - платеж (выигрыш, проигрыш);парная антагонистическая игра с нулевой суммой - выигрыш 1-го игрока=платежу (проигрышу) 2-го;партия игры - опред последовательно-сть ходов (действий игроков), завершающаяся процедурой выявления платежа; хар-р ходов опред-ся правилами игры; по кол-ву ходов в партии их делят на одноходовые и многоходовые; в теории игр исходят из многократной повторяемости партий (операций);выбор хода мб осущ-ён сознательно или случ образом (бросание костей, рулетка и др.); игры, сост-щие только из случ ходов не явл предметом теории игр;игры с полной и непол инф-ей - соответствуют сит-ям различ степени информирти игроков о последствиях (рез-те) всех предшествующих и возм-х тек-х и буд-х ходов (случайных и сознательных) игроков;стр игрока – совокуп-ть правил, однозначно определяющих выбор игроком возм-го вар-та действий (хода) при каждом сознательном ходе в завис от конкрет сложившейся сит в партии; другое её название - чистая стр; чистая стр не исп-т Эл-ы случ выбора;способ действий - совпадает с понятием стр для игр с одноходовыми партиями; для случая многоходовых партий способ действий представляет собой опред Эл-т стр;смешанная стр - сл стр, сост в случ-м чередовании неск-х чистых стр-й с опред вероятностями (частотами);игра конечна, если число возм-х стр (чистых) у каждого игрока конечно;партия определена, если выбраны стр игроков в партии (рез-т партии при этом колич-но определён);игра определена, если перечислены все возм стр игроков (множества Х и Y) и задана соответствующая ф-я платежа L(X,Y);формальное задание парной конеч антагонистической игры с нулевой суммой осущ-ся заданием стр игроков и платёжной матрицы: X=(x1,x2,...,xm), Y=(y1,y2,...,yn),
цель теории игр - выработка рекомендаций по выбору наилучшего поведения участников многократно повторяющейся конфликтной ситуации; задача теории игр - нахождение решения игры - наилучшей (оптимальной) стратегии для каждого игрока; цена игры - размер платежа, соответствующий лучшим (оптимальным стратегиям). Основные принципы, учитываемые при поиске наилучшей стратегии: каждый игрок считает своего противника разумным (принцип предсказуемости поведения); каждый игрок стремится обеспечить себе некоторый гарантированный (независимый от поведения противника) результат (принцип гарантированного результата). В теории не учитываются промахи и ошибки игроков, элементы азарта и риска в конкретных ситуациях. Оптимальная стратегия- такая стратегия, которая обеспечивает игроку максимально возможный средний выигрыш. Устойчивость оптимальных стратегий игроков определяется невыгодностью отклонений от них - они ведут к снижению среднего выигрыша. Теорема о существовании решения игры - любая конечная антагонистическая игра имеет решение в области чистых или смешанных стратегий. 65 Понятия максимина и минимакса как стратегий предельной осторожности оперирующих сторон. Понятия максимина (нижней цены игры) - элемент платёжной матрицы, для которого достигается максимум минимальных значений элементов по строкам. Понятие
минимакса
(верхняя цена игры) - элемент платёжной
матрицы, для которого достигается
минимуму максимальных значений
элементов по столбцам.
Очевидно,
существуют стратегии предельной
осторожности для игроков; максиминная
- для игрока 1, минимаксная - для игрока
2. Эти стратегии гарантируют определённый
результат для каждого игрока, не
зависящий от действий противника.
Если 1=2,
то соответствующий элемент платёжной
матрицы называют седловой
точкой
игры. Седловая точка является элементом,
на котором одновременно достигается
минимум в столбце и максимум в строке
платёжной матрицы; его значение равно
чистой
цене
игры.
Если платёжная матрица имеет седловую
точку, то игра имеет решение в чистых
стратегиях. Пусть игра не имеет седловой
точки и, следовательно, 1<2.
При выборе стратегий предельной
осторожности остаётся область
неопределённости - неясно, возможно
ли определённым чередованием чистых
стратегий обеспечить выигрыш, больший
1(проигрыш,
меньший 2).
Дополнительным поводом для таких
рассуждений является неустойчивость
максиминной и минимаксной стратегий
- отклонения от них не всегда приводят
к ухудшению результата для игроков.
Оказалось, что в играх без седловых
точек существует решение в смешанных
стратегиях. Игроки в случае отсутствия
седловой точки должны держать в
секрете выборы своих ходов в каждой
партии игры и самый надёжный путь -
случайный выбор хода; при этом оба
игрока не знают конкретного выбора
ходов в партии. Смешанные стратегии
игроков принято задавать в форме
вероятностей (относительных частот)
применения ими чистых стратегий. Активные стратегии - чистые стратегии, входящие в состав оптимальной смешанной стратегии с ненулевыми частотами. Оптимальная смешанная стратегия обладает свойствами: устойчивость - отклонение от оптимальной стратегии ведёт к снижению результата для каждого из игроков; цена игры удовлетворяет условию 1<<2; если игрок пользуется своей оптимальной смешанной стратегией, выигрыш остаётся неизменным и равным цене игры, независимо от действий второго игрока, если последний не выходит за пределы своих активных стратегий.
67 Особенности игры с природой. Понятие матрицы риска. Кроме неопределённых факторов, рассматриваемых в конфликтных операциях, связанных с неизвестными действиями разумных и активных противников, существуют неопределённости другого типа: недостаточная осведомлённость оперирующей стороны об условиях операции, не зависящих от сознательно противодействующей стороны, а зависящей от неизвестной объективной реальности - "природы". "Природа" - незаинтересованная субстанция, действия которой неизвестны, но не содержит элементов враждебности и противодействия. Постановка задачи. Оперирующая сторона располагает стратегиями X=(x1,x2,...,xm), недостаточно известные состояния природы характеризуются предположениями П=(П1,П2,...,Пn). Их следует рассматривать, как возможные стратегии природы. Платёжная матрица имеет обычный вид: А={aij}, i=1,2,...,m; j=1,2,...,n. Кроме платёжной матрицы оперирующая сторона может иметь и некоторые априорные оценки о вероятностях возможных состояний природы, т.е. располагать вектором Q={qj}, j=1,2,...,n. Здесь qj - оценка вероятности состояния природы Пj. Точность таких оценок может быть различна и могут быть ситуации, когда исследовательской группе доступны эксперименты с целью уточнения этих оценок (действия малыми средствами). Имеются определённые особенности такой постановки, связанные с возможностями большего выигрыша, чем в игре с сознательным противником; большими трудностями обоснования лучших стратегий, меньшими возможностями сокращения размерности задач. Во многих ситуациях целесообразен переход от платёжной матрицы к матрице рисков, ибо платёжная матрица может формировать искажённые представления относительно выгодности отдельных стратегий. Предположим, что выигрыш при стратегии Xi и состоянии природы Пj оказался выше, чем при выборе стратегии Xk и состоянии природы Пl, т.е. аij>аkl. Однако более высокий выигрыш может не быть результатом удачного выбора стратегии, а следствием другого обстоятельства: ситуация Пj вообще более выгодна для операции в сравнении с ситуацией Пl. Например, состояние природы с отсутствием отрицательных тенденций рыночных условий для конкретной торгово-закупочной операции всегда более выгодна, чем ситуация с резким падением цен на реализуемую продукцию. С целью устранения подобных искажений в теории статистических решений введено понятие "риска". Риском Rij игрока 1 при использовании стратегии Xi в условиях Пj называют разность между максимальным выигрышем, возможным в ситуации Пj, и выигрышем при выборе стратегии Xi: Rij=Lj-аij, где Lj - максимально возможный выигрыш в ситуации Пj, то есть: Lj = MAX аij 1<=i<=m Величина Lj является таким образом оценкой благоприятности состояния природы Пj для осуществления операции. Очевидно, что Rij0. Виды игры без экспериментов в зависимости от наличия априорной информации о возможных состояниях природы - три случая: 1) имеется априорная информация о вероятностях возможных состояний природы в форме вектора Q={qj}, j=1,2,...,n; 2) априорная информация отсутствует, но имеются основания для гипотез относительно вероятностей возможных состояний природы; 3) информация о вероятностях возможных состояний природы полностью отсутствует. Первый случай является наиболее простым и формально не отличается от рассмотренной ранее задачи с вероятностным заданием исходов операции; однако в данном случае информация о вероятностях исходов характеризуется существенной недостоверностью. Таким образом, модель игры с природой без эксперимента при наличии априорных оценок о вероятностях возможных состояний природы формально совпадает с моделью принятия решений в условиях заданной вероятности неопределенных факторов. Вариант модели для случая максимизации среднего выигрыша опирается на концепцию оптимизации в среднем - так называемый байесовский подход (соответствующие оптимальные стратегии называются байесовскими):
Анализ варианта модели для случая минимизации среднего риска показывает, что оптимальные стратегии для обоих типов моделей совпадают:
70 Возможности применения критериев, отражающих нестабильность доходов (риск) оперирующей стороны при выборе решения в условиях стохастичности. Принятие решений в условиях стохастической природы влияющих факторов основывается на использовании критериев, учитывающих известные законы распределения значений этих факторов. Статистические характеристики - математическое ожидание, дисперсия и др. применяются для определения стратегий и управлений, лучших в заранее определённом смысле. Однако, несмотря на хорошую изученность управляемых процессов, в данной ситуации оперирующая сторона всегда рискует получить не тот результат, на который она ориентируется при выборе. Это связано со случайным характером исходов операции. Ещё большим риском сопровождается выбор решений в условиях неопределённости. Однокритериальные статические ЗПР в детерминированных условиях исследуются методами МП. В условиях риска применяются методы теории вероятностей, теории игр, статистических решений и др., а также экспертные методы. Следует иметь ввиду, однако, что любая реальная ЗПР обычно удовлетворяет нескольким признакам классификации и представляет собой смешанный тип ЗПР. Сложнейшим вопросом, возникающим в реальных ЗПР, является поэтому определение понятия "наилучшее" решение; особый характер приобретают эти затруднения в случае неопределённости и многокритериальности. Только после решения этой проблемы (хотя бы в предварительного, концептуального) возможно решение вопросов формально-математического характера: построение схемы расчётов, выбор методики и методов поиска решений и т.п. Известно общее положение: полностью может быть формализован поиск наилучших решений только в случае простейшего класса ЗПР - однокритериальных детерминированных; все другие постановки обязательно предполагают применение неформальных (экспертных, эвристических, эмпирических) процедур. Для задач МП также имеется определённая градация по сложности их содержания и применяемых методов: линейные, квадратичные, выпуклые, сепарабельные, нелинейные общего вида. Для задач МП последнего типа применяют (в случае их полиэкстремального характера) методы поиска экстремумов (градиентные, наискорейшего спуска, покоординатной оптимизации, овражные, случайного поиска с адаптацией и т.п.).
44(Метод сценариев учета неопределенности в моделях, его модификации и совмещение с вероятностными подходами). Модель развития и размещ-я пр-ва.
Ф-я
цели
50 Характеристика процессов многошагового принятия решений, описание динамической модели (ДП), используемые гипотезы и определения. Модель многошагового процесса принятия решений. 1. В качестве примера рассмотрим модель динамического программирования. Краткое описание ее принципов и свойств: - процесс управления может быть разделен на отдельные этапы (шаги), их число обычно конечно; - управляемая система переходит из некоторого начального состояния W0 (или множества начальных состояний) в некоторое конечное состояние Wn; тогда W1,W2,...,Wk,...,Wn - состояния системы в конце 1-го, 2-го, ..., n-го шага процесса управления; - для любого (k-го) шага состояние системы в конце шага описывается конечным набором параметров; обозначим их через Vk1,Vk2,...,Vks; они называются фазовыми координатами (геометрически отображаются точкой S-мерного фазового пространства); - преобразование системы по шагам осуществляется с помощью управлений (мероприятий) U1,U2,...,Un; их совокупность образует управление системой в целом (вектор управления U=(U1,U2,...,Un)); - управление Uk на к-м шаге преобразует систему из состояния Wk-1 в состояние Wk и заключается в выборе значений переменных управления Uk1,Uk2,...,Ukl. - пусть состояние системы в конце к-го шага (любого) зависит только от состояния к началу этого шага Wk-1 и выбранного на нем управления Uk; т.е. Wk = F(Wk-1,Uk), k=1,...,n (1) Это свойство системы называется отсутствием последействия. - цель процесса управления - достижение некоторого эффекта Z, считаем его зависящим от начального состояния системы W0 и реализованного управления U. - пусть функция цели управления Z=G(W0,U) обладает свойством аддитивности, т.е. полный эффект от управления U является суммой частных (локальных) эффектов, полученных на отдельных шагах процесса: n Z = SUM fk(Wk-1,Uk) (2) k=1 где fk(Wk-1,Uk) - эффект от управления на к-м шаге; - в конкретных задачах управления, выбираемые на каждом шаге, не являются произвольными, они должны удовлетворять определенным ограничениям; такие управления называются допустимыми; - задача многошагового выбора решений формулируется следующим образом: определить допустимые управления U1,U2,...,Uk,...,Un, переводящие систему из начального состояния W0 в конечное состояние Wn и обеспечивающие максимальную эффективность в смысле (2). Соответствующее управление называется оптимальным, обозначим его через U^=(~U1,~U2,...,~Uk,...,~Un); - начальное и конечное состояния могут быть заданы однозначно либо указаны множества возможных состояний системы в начале и конце процесса W0@R0, Wn@Rn; - в зависимости от характера переменных управления, числа фазовых координат s, задачи ДП делят на непрерывные и дискретные, одномерные и многомерные; - в основе методов решения задач ДП лежит принцип Бэллмана: каково бы ни было состояние системы к началу любого к-го шага процесса, выбираемое на нем управление Uk должно быть оптимальным не только относительно данного шага (исходя из эффекта на данном шаге), но и с учетом всех последующих управлений. Принцип отражает тот факт, что выбор управления на текущем шаге производится с учетом эффектов, получаемых не только на этом шаге, но и на всех будущих шагах процесса; - формальные определения для описания метода решения задачи ДП: суммарный эффект от управления на шагах с (к+1)-го по n-ый составит n Zk+1 = SUM fi(Wi-1,Ui) (3) i=k+1 Если известно оптимальное управление на этих шагах (т.е. ~Uk+1,...,~Un), то получим условный максимальный эффект на этих шагах (зависящий от состояния системы к началу к-го шага) MAX Zk+1 = ~Zk+1(Wk) С другой стороны, состояние Wk зависит от выбора управления Uk на к-м шаге процесса и, согласно принципу Бэллмана, это управление надо выбирать с учетом эффекта на всех будущих шагах - с (к+1)-го по n-ый: ~Zk(Wk-1) = MAX fk(Wk-1,Uk)+~Zk+1(Wk) (4) Uk k=1,...,n-1 Таким образом получим условный максимальный эффект на шагах с к-го по n-ый. Аналогичные уравнения составляются для всех шагов с 1-го по (n-1)-ый. Для последнего n-го шага имеем ~Zn(Wn-1) = MAX fn(Wn-1,Un) (5) Un Получим систему последовательно связанных (реккурентных) уравнений Бэллмана, очевидно, что решив последнее из них (условный максимум функции одной переменной) и подставив решение в предыдущее, получаем возможность решить (n-1)-ое уравнение и т.д. до 1-го. Таким образом получаем последовательность условных максимальных эффектов на шагах с n-го по 1-ый: ~Zn(Wn-1),~Zn-1(Wn-2),...,~Zk(Wk-1),...,~Z1(W0). Однако по определению ~Z1(W0) есть максимальный эффект на шагах с 1-го по n-ый, т.е. за весь процесс,причем исходное состояние W0 либо задано, либо может быть определено дополнительным расчетом. Следовательно, имеем максимальный эффект и оптимальное значение функции цели ~Z. Этот этап называется этапом условной оптимизации; из решения уравнений одновременно определяются и условные оптимальные управления на всех шагах: ~Un(Wn-1),...,~Uk(Wk-1),...,~U1(W0). На втором этапе - безусловной оптимизации, начиная с первого шага определяют оптимальное управление на этом шаге; подставляя результат в уравнение состояния системы для первого шага (1), определяем состояние системы к началу второго шага, и определяем оптимальное управление на втором шаге из функции ~U2(W1) и т.д. Такая схема расчетов называется методом обратного хода. Условия сводимости задачи к многошаговой модели выбора решений. - аддитивность функции цели; - независимость структуры задачи от конкретного значения n; - конечность задачи,т.е. ее описание конечным числом параметров состояния и переменных управления; - условие "отсутствия последействия"; - ограничения на эффективность, связанные с типом задачи и ее размерностью. 62 Задача управления запасами как модель ДП в форме метода прямого хода. Модель управления запасами при заданном расходе а) задачи управления запасами - характерная сфера применения моделей и методов ДП; причины - естественность разворота процесса управления запасами во времени; управление на каждом шаге зависит от уровня запасов к началу шага и возможным расходом на этом шаге и последующих шагах; обычен дискретный характер переменных управления, параметров состояния; форма зависимостей очень проста. б) вводные определения - запасы, уровень запасов, зависимость его от пополнения и расхода за предыдущий период и начального уровня; управление запасами через воздействие на пополнение и расход; цель управления - оптимизация некоторого критерия, зависящего от пополнения и расхода - затрат на хранение и поставку, потерь и штрафов от недостаточного уровня запасов, снижения объемов производства и т.п., либо суммарный эффект от реализации запасов с учетом затрат на их хранение и пополнение. в) случай заданного расхода: управление сводится к пополнению; рассматривается период из n-шагов, задан расход на каждом шаге Dk, k=1,2,...,n; известен начальный уровень запасов Е0 и зависимость затрат на хранение и пополнение на каждом шаге от их объемов; требуется найти размеры пополнения на каждом временном промежутке при условии обязательного удовлетворения расхода и минимизации суммарных издержек за весь период; г) модель имеет вид: Хк - размер пополнения запасов на к-м шаге процесса; Ек-1 - уровень запасов к началу к-го шага процесса; суммарные затраты на хранение запасов в к-м шаге можно оценивать вличиной, зависящей от среднего уровня запасов на шаге, например, считая его равным ^Ek = Ek-1 + Xk/2; тогда затраты на хранение и пополнение в к-м шаге имеют форму Fk(^Ek,Xk)=Fk(Ek-1,Xk) Функция цели задачи имеет вид n Z= SUM Fk(Ek-1,Xk)----->MIN k=1 Уравнения состояния системы имеют вид: Ek = Ek-1 + Xk - Dk, k=1,2,...,n их удобнее представлять в форме Ek-1 = Ek -Xk + Dk, k=1,...,n т.е. через параметры конца шага; Условия допустимости выбираемых управлений: Хк >= 0, Ek >= 0, k=1,...,n; это следует из необходимости удовлетворения заданных расходов; следовательно, и Ek-1 >= 0, а значит имеем Xk <= Ek + Dk, k=1,2,...,n При решении частных задач на этапе условной оптимизации считаем, что уровень запасов к концу шага Ек задан как параметр, поэтому функцию затрат тоже удобнее представить в форме зависимости от уровня запасов к концу шага, т.е. Fk(Ek-1,Xk) = Fk(Ek-Xk+Dk,Xk) = Fk(Ek,Xk), k=1,...,n д) так как известно начальное состояние запасов Е0, но ничего не задано относительно конечного их уровня Еn, то формулировку уравнений Бэллмана удобнее осуществить для метода прямого хода: k ~Zk(Ek) = SUM Fi(Ei-1,~Xi) - условные минимальные затраты на шагах i=1 с 1-го по к-ый (зависят от параметра Ек); Тогда уравнения Бэллмана имеют вид: ~Z1(E1) = MIN F1(E0,X1) = MIN F1(E1,X1) k = 2,3,...,n X1 X1 е) на этапе условной оптимизации, осуществляемом с первого шага, получим последовательность функций, зависящих от одного параметра - уровня запасов к концу соответствующего шага - условные минимальные затраты и условные оптимальные пополнения: ~Z1(E1),~Z2(E2),...,~Zk(Ek),...,~Zn(En --------------------------------------- ~X1(e1),~X2(E2),...,~Xk(Ek),...,~Xn(En) Так же как и в методе обратного хода по завершению этапа значение критерия может остаться неопределенным, если не фиксировано значение Е0 в прямом ходе или Еn - в обратном ходе; тогда по окончании этапа условной оптимизации в обоих случаях решают вспомогательные задачи на выбор Е0 или En. ж) на этапе безусловной оптимизации, начинающейся с n-го шага последовательно получаем оптимальные пополнения запасов: ~Xn = ~X(~En), где ~Еn либо задано либо определено по специальному расчету ~Еn-1=~Еn-~Хn+Dn ~Xn-1 = ~X(~En-1), ~Еn-2=~Еn-1-~Хn-1+Dn-1 ~Xn-2 = ~X(~En-2), ~Еn-3=Еn-2-~Хn-2+Dn-2 .............................................. ~X1 = ~X(~E1), ~Е0=~Е1-~Х1+D1
56 Схема обратного хода расчетов по модели ДП – содержание этапа безусловной оптимизации. Схема
решения: задача решается с последнего
хода. МЕТОД ОБРАТНОГО ХОДА.
Множество
возможных состояний Е В результате решения получается несколько решений (множество рез-ов)
Прейдя
к первому шагу найд-ся благ-т решение
58 Схема прямого хода расчетов по модели ДП и ее отличия от схем обратного хода. I
этап
(условной оптимизации)
1
шаг:
II
этап: (безусловной оптимизации)
|
47 Основные понятия теории принятия решений – стратегия, альтернатива, способ действий, оперирующая сторона и операция, цели и критерии. Осн опред и термин, использ-е в теории принятия реш. 1) Операция – орган-ая деят в любой сфере, объединённая единым замыслом, целями, имеющая х-р многократности (повторяемости). Предполагается возможность кол-ной оценки многих важн хар-тик операции научными методами. В отд уникальных сит требование повторяемости смягчается - оно предпол-ся необх-м для составл-х частей всей операции, иначе исчезают основания для кол-й оценки сит и реш во многих приложениях – эк-ке, торговле, транспортировке и т.п.Повторяемость операций в бол-ве сит обусловлена их содержанием - массовостью и непрерывностью производства, обращения, реализации, распределения, инвестирования и др. Примеры операций: произв деят, инвестиц деят, сов-сть мероприятий по повышению платёжеспособности и фин устойчивости и т.п. 2) Оперирующая сторона - сов-сть лиц и технич ср-в, исп-мых для целей упр-я, кот стремятся в данной операции к достиж целей (ЛПР, министерства, администрация предприятия и др.). Возможно наличие неск-х оперирующих сторон в одной операции, им-х различные полностью или частично цели. Такая ситуация называется конфликтной, а такие операции - многосторонними или конфликтными. В операциях возм-но участие арбитров или прир сил, повед кот не подчинено стремлению к достиж целей оперирующих сторон. Достиж целей невозможно без затрат рес-в: сырья, машин, оборудов, раб силы, ден ср-в и др. 4) Операция- управляемый процесс; оперирующая сторона управляет операцией, выбирая способы исп-ния рес-в - способы действий. В качестве синонимов применяют термины: альтернатива, управление, стратегия, решение.Возм-ти упр (оперирующей) стороны всегда ограничены в силу ряда естественных причин, вытекающих из ограниченности рес-в - этим опред-я так называемые "дисциплинирующие" усл выбора способов упр (стратегий). Стратегии, удовлетворяющие ограничивающим усл-м называют допустимыми. Понятие допустимости является относительным - совокупность допустимых управлений меняется с изменением ограничений. Реал-я опред допустимых стра приводит к различным исходам операции. Для сравнения стр треб-ся возм-ть оценивать исходы. Этот процесс осущ-ся с пом критериев.Стратегии (решения, управления) лучшие в смысле принятых критериев называют оптим-ми (рац-ми, наиболее приемлемыми и т.п.). Эти понятия также имеют относительный характер.В составе оперирующей стороны выд-ся исследов-кая гр; следуя тем же целям, эта гр не принимает окончат-х реш, а лишь колич-но и кач-но их обосновывает. Эти обоснования не могут иметь исчерпывающий хар-р и для их большей надёжности исследовательская группа освобождается от ответств-ти за принятие окончат-х реш. Рук-ль операции (ЛПР) учитывает рекомендации и обоснования исследоват-й гр; исследоват-й гр-й д. прим-ся методы, допускающие проверку рез-в другими независимыми исследователями.Не сущ-ет единой общей технологии ППР, однако имеются достаточно апробированные предложения; в целом аналогичны по струк схемы, предлагаемые многими специалистами по исследованию операций и упр произв-м. Такие схемы обычно включают этапы:предварит форм-ка проблемы;опред целей операции и выбор критериев отбора реш;выявл и форм-ка ограничений;разраб-ка полного состава альтернатив и их предварительный ан;сбор инф и прогноз-е параметров операции в буд-м;уточнение форм-ки проблемы;разраб-ка модели операции, позволяющей оценивать альтернативы; ан и выбор схемы модельных расчётов и исслед-й;оценка и хар-ка альтернатив;разраб-ка рекомендаций с учётом доп данных о последствиях принятия реш; 69 Байесовский подход к поиску лучшей стратегии в условиях стохастической неопределенности возможных условий экономической операции, его достоинства и недостатки. Принцип Байеса: оптимальной считается стратегия обеспечивающая максимальный средний доход за достаточное повторение экономических операций. Это макс матем ожидания дохода. Средний доход, фор-ла Байоса: ∑qja1j=a1ср. Вероятность – частота получения ∑ qjaij= aiср, i=1,5,max∑ qjaij= max aiср=amaxср. при большом повторении в стабильной эк-ой ситуации обеспечим средний макс доход в 19,66. Достоинства: 1. Обеспечим макс среднего (и наиболее вероятного) дохода. Недостатки: Возможная нестабильность результатов по отдельным операциям. Нестабильность характеризуют дисперсия, стандартное отклонение, коэффициент вариации. Найти частоты таким образом что бы 1. макс средний доход при заданном ограничении на риск 2. мин средний риск при заданном уровне дохода. 1. вероятность q=(q1….qn). 2. qj, j-1,n – недостоверность (ненадежность) 3. нет гипотез в пользу большей или меньшей достоверности отдельных ситуаций. В этом случае их можно считать равновероятными. Qj=1/n, можно использовать Байоса и его модификации. 4. Имеются гипотезы в соответствии с которыми ситуации можно упорядочить по их вероятностям Sj, j=1,n I=(n, n-1, n-2…1) Если они упорядочены по вероятностям мы можем использовать в расчетах. Мы можем рассчитать условные вероятности ситуации n(n+1)/2, n, n-1, n-2…1. ∑=n(n+1)/2=Z, q=n/z, q2=n-1/2, qn=1/z Что бы снизить неопределенность выбора. 38 Применение межотраслевого баланса при анализе и прогнозировании народнохозяйственных пропорций. Понятие чистой и хозяйственной отрасли МОБ. В МОБ используются только чистые отрасли. Чистая отрасль - совокупность производства данного вида продукции. Продукция, которая составляет наибольший удельный вес в валовом выпуске отрасли, дает название этой хозяйственной отрасли. Помимо этой профилирующей продукции хозяйственная отрасль выпускает ряд товаров, на производстве которых специализируются другие хоз. отрасли ( например, автомобилестроение). Установление взаимно однозначного соответствия между наименованием отрасли и наименованием продукции, которую отрасль производит, означает переход от хозяйственных отраслей к чистым. Это соответствие достигается, если: каждая отрасль производит только один продукт; 2) каждый продукт производится только одной отраслью Эти условия означают, что продукция, включенная в вал.выпуск “чист. отр.”, должна быть по возможности однородной и этот вид продукции не должен производиться другими отраслями. Реально чистых отраслей не существует, это теоретическое понятие. Пример: АМО “ЗИЛ”: по юридическому статусу предприятие выпускает автомобили (“чистая” отраслевая направленность), но фактически помимо автомобилей выпускает и холодильники и др. продукцию (хозяйственная направленность). 46 Модель рационализации регионального баланса котельно-печного топлива (КТП). КПТ (нефть, магт, торф, прир газ и т.д.). Потребители в модели группируются (мелкие), а крупные рассматриваются отдельно. Все ЭС <мВ – объединяют в одну группу; Все ЭС >50МВ – рассм отдельно. Котельные в городе объединяют в группу КОМБЫТ (коммун бытов потребит). Прямое производственное потребление: - обжиговые печи - нагревательные печи и т.д. Если в модели база берется 2005г, то о 2010 –расмотрение по годам, дальше до 2015, 2020 (по 5 лет). Потребители Виды топлива э/э газ угли торф э/э КПТ газ угли торф Модель в мат виде: Рес-сы КПТ: i=1,m – индекс конкретного вида КПТ; j=1,n- потребители. dj – спрос потребителей в полезном топливе (в ту.т.) Bj - объем рес-сов (собств рес-сы + остат на нач + поставки со стороны – наши поставки на сторону –переходящ остаток на кон) Xij- поставки итого рес-са джитому потребителю
Баланс по потребителям:
Баланс по ресурсам:
Возможные критерии: стоимостной: есть цена на каждый вид топлива и тарифы на ж/д перевозки (н учит-ть скидки) + сами продавцы устан-ют цены на газ, э/эн (тарифы на газ и Эл/эн учит-ют сразу и транспортировку, тарифы на топливо состоят из 2х частей). Минимум – суммарные издержки на обеспечение территории КПТ. Возможны частные противоречия, но они всё равно используютя.
48 Применение модели рационализации баланса КТП для оценки направлений развития топливной отрасли и электроэнергетики. КПТ (нефть, магт, торф, прир газ и т.д.). Потребители в модели группируются (мелкие), а крупные рассматриваются отдельно. Все ЭС <мВ – объединяют в одну группу; Все ЭС >50МВ – рассм отдельно. Котельные в городе объединяют в группу КОМБЫТ (коммун бытов потребит). Прямое производственное потребление: - обжиговые печи - нагревательные печи и т.д. Если в модели база берется 2005г, то о 2010 –расмотрение по годам, дальше до 2015, 2020 (по 5 лет). Потребители Виды топлива э/э газ угли торф э/э КПТ газ угли торф Модель в мат виде: Рес-сы КПТ: i=1,m – индекс конкретного вида КПТ; j=1,n- потребители. dj – спрос потребителей в полезном топливе (в ту.т.) Bj - объем рес-сов (собств рес-сы + остат на нач + поставки со стороны – наши поставки на сторону –переходящ остаток на кон) Xij- поставки итого рес-са джитому потребителю
Баланс по потребителям:
Баланс по ресурсам:
Возможные критерии: стоимостной: есть цена на каждый вид топлива и тарифы на ж/д перевозки (н учит-ть скидки) + сами продавцы устан-ют цены на газ, э/эн (тарифы на газ и Эл/эн учит-ют сразу и транспортировку, тарифы на топливо состоят из 2х частей). Минимум – суммарные издержки на обеспечение территории КПТ. Возможны частные противоречия, но они всё равно используютя. Электроэнергетика: Сложность выявления количественных взаимосвязей при прогнозе энергоэкономических тенденций связана главным образом с неопределенностью будущих условий развития и исходной информации. Она усугубляется в кризисные периоды при смене политических и экономических парадигм. Поэтому существует проблема определения энергоэкономических пропорций в зависимости от тех или иных тенденций развития экономики. Приходится с помощью какого-либо формального инструмента имитировать основные энергоэкономические взаимосвязи в перспективном периоде. В современной ситуации в качестве такого инструментария может использоваться имитационный подход к моделированию и прогнозу энергоэкономических пропорций. Для прогноза энергоэкономических пропорций наиболее используемыми являются эконометрические модели и балансовые типа “затраты-выпуск”. Некоторые аспекты энергоэкономической динамики можно исследовать с помощью модели оптимизации топливно-энергетического комплекса (ТЭК). В период значительной нестабильности экономики целесообразно применять моделирование для ориентировочной оценки энергопотребления. С этой целью можно использовать соответствующим образом модифицированную модель межотраслевого баланса (МОБ), в мировой практике —модель “затраты-выпуск”. Отметим следующие преимущества ее применения: — возможность взаимоувязанных исследований вещественных пропорций экономического роста, технологических изменений, динамики +цен на энергетическую и неэнергетическую продукцию; — сценарные варианты могут формироваться с целью осуществления как нормативного, так и исследовательского прогноза электропотребления; — возможность объективно оценить, насколько развитие региональных отраслей ТЭК будет соответствовать темпам экономического роста в регионе; — несложность модификации модели позволяет дополнять ее по мере подготовки информации различными блоками, например, экологическим, инвестиционным, основных производственных ресурсов и т.д.; — целевая функция, вводимая в модель, дает возможность осуществлять расчеты с помощью разнообразных критериев в зависимости от приоритетных направлений развития экономики и энергетики региона.
60 Требования к формулировке экономических проблем, выполнение которых является необходимым для их формализации в виде моделей ДП. 1).аддитивность
функции цели(общий эффект,как сумма
эффектов по отдельным шагам);2).процесс
принятия решения может рассматриваться
как многошаговый(n-конечн.);3).отсутствие
последействия;4).число параметров
состояния и управления одинаково на
каждом шаге.
64 Задачи рациональной замены оборудования, модернизации производства в форме моделей ДП. Необходимые общие сведения по проблеме. 1.Актуальность проблемы, особенно в в периоды достаточноой стабильности общих экономических условий и рыночной конъюнктуры, обусловлена действием следующих факторов: - 1)физическим и моральным износом оборудования, приводящим к росту издержекна ед. выпускаемой продукции (повышение затрат на ремонт и обслуживание, снижение производительности и рост простоев), к снижению качества выпускаемой продукции, ограничению возможностей обновления продукции по качеству и ассортименту;- 2)моральное старение технологий связано с невозможностью применения новых машин и оборудования, особенно в виде полной, а не частичной его замены в технологических цепочках; это ограничивает возможности запуска в производство новых и улучшенных видов продукции, имеющих повышенный спрос, удовлетворяющие современным требованиям к качеству, безопасности применения,экологичности и т.п.;- 3)старение структуры выпускаемой продукции снижает финансовую устойчивость предприятия, ухудшает его позиции на рынке, ведет к снижению престижа фирмыи снижению объема продаж;- 4)более высокая производительность, экономичность и экологичность новых машин и оборудования, их ориентация на применение в современных прогрессивных технологиях, более высокая надежность в эксплуатации, более высокие параметры качества в применении предопределяют необходимость вложений в совершенствование и развитие производства;- 5)очевидно, что процесс совершенствования и развития производства, непрерывный в целом, можно разделить на отдельные этапы (шаги), в течение которых технологии, продукция, оборудование сохраняются,и заменяются на других шагах новыми. Целесообразность такой замены (обновления, модернизации и т.п.) определяется с учетом ряда взаимодействующих факторов, которые часто зависят от времени. Момент времени, к которому должна быть осуществлена замена,можно оценить на основе расчетов по специализированным динамическим моделям. Такие модели и расчеты могут быть как детализированными, так и достаточно укрупненными. Первые детально учитывают все основные факторы, оказывающие влияниена эффективность процесса замены (в т.ч. согласованность отдельных этапов замены во времени), вторые предназначены для предварительной оценки сроков осуществления мероприятий по развитию и совершенствованию производства и применяются главным образом для перспективной предварительной проработки направлений развития производства. Однако для всех типов таких задач характерным является естественное разворачивание во времени процесса управления и применимость для расчетов процедур и принципов ДП - прежде всего, в связи с нелинейным и дискретным характером процессов замены, а, следовательно,невозможностью применения классических методов оптимизации. 2. Общее описание модели (простейший случай) В качестве критерия выбора варианта замены чаще всего применяют либо прибыль от эксплуатации оборудования (с учетом всех негативных последствий сохранения устарелых его систем), либо суммарные затраты на его эксплуатацию и обслуживание в течение рассматриваемого времени прогноза. Выбор и обоснование периода прогноза является самостоятельной проблемой и определяется не только параметрами технического прогресса в данной сфере деятельности, динамикой экологических норм и требований безопасности, но и характеристикой ситуации на рынке и ее тенденциями, динамикой общей экономической конъюнктуры и стратегией (целями) фирмы на ближайший и отдаленный периоды. Процесс применения производственных систем (оборудования и технологий, определенных видов продукции) рассматриваем как n-шаговый: период прогноза разбивается на n временных промежутков (в зависимости от детализации прогноза и масштаба оцениваемых мероприятий это могут быть годы,кварталы,месяцы и т.п.). В начале каждого промежутка-шага может быть принято решение о сохранении прежней системы либо о ее замене, причем термин "замена" имеет здесь условный характер - это может быть реконструкция, модернизация, частичная или полная замена оборудования, модернизация изделий или снятие их с производстваи т.п.). Управление на каждом шаге состоит, таким образом, из нескольких альтернативных решений. Принципиальная схема модели не зависит от количества рассматриваемых альтернатив, поэтому, с целью упрощения схемы рассуждений, мы ограничимся изложением простейшего случая - предположим, что на каждо шаге имеются только два альтернативных решения: сохранение старой системы или ее замены. Очевидно, что замена системы не может осуществиться мгновенно, для этого необходим определенный период времени; и,если затраты на замену, потери связанные с временным снижением выпуска продукции за период освоения новой системы несложно учесть в экономических характеристиках сооответствующего шага, то период времени, в течение которого осуществляется замены не должен в модели превосходить по длительности выбранного шага расчетов. В противном случае нарушается принятая для моделей ДП гипотеза "отсутствия последействия". Впрочем, для того,чтобы остаться в рамках модели ДП, можно пойти на "диверсификацию" алтернативы "замена", разделив ее условно на несколько последовательно связанных альтернатив (в форме цепочки). Каждая из таких альтернатив в модели считается формально независимой, однако они связаны общим конечным эффектом, который достигается на последнем шаге цепочи. Промежуточные шаги цепочки, наоборот, увеличивают издержки процесса, однако принцип Беллмана позволяет учесть эффективность цепочки в целом при условии строгого описания допустимых управлений на всех шагах. Это описание включает запрет на нарушение прямой последовательности отдельных шагов-элементов цепочки; временные разрывы между отдельными элементами цепочки могут допускаться и регулируются размером дополнительных издержек от замораживания средств. Обозначим решение о замене через Uз, решение о сохранении - через Uc. Функциональные уравнения на каждом шаге содержат в нашем случае только две величины, которые необходимо сопоставить между собой: первая - эффект при при выборе управления Uз, вторая - эффект при выборе управления Uc. Очевидно, что условная оптимизация на каждом шаге, состоящая в сравнении этих величин и выборе из них наилучшей не является трудоемкой.
53 Общая постановка многокритериальной задачи выбора решений. Необходимость компромисса и его возможные принципы. Понятие областей согласованности и противоречивости критериев. Область эффективных решений и способы ее построения. Рассматривается управляемая операция, исход которой зависит от действий оперирующей стороны; условия процесса достаточно изучены. Эффективность управления оценивается совокупностью показателей-критериев E1,E2,...,Ek, образующих вектор E=(Eq), q=1,...,k Иногда бывают известны из предшествующего опыта и показатели относительной важности (значимости) критериев H1,H1,...,Hk, образующих вектор H=(Hq), q=1,...,k. Каждый частный критерий характеризует уровень достижения некоторой частной (локальной) цели операции - пример - выбор конструкции самолета. Приведем необходимые сведения по проблеме. 1)Зависимость значений каждого частного критерия от решений оперирующей стороны (определяемого вектором Х=(Х1,Х2,...,Хn)) могут быть заданы в различной форме - аналитически, графически, таблично, специальными процедурами, например, решениями задач ЛП.2)Цель управления определяется в увеличении возможных значений всех критериев, однако одновременное достижение наилучших значений по всем целям обычно невозможно за счет выбора одного решения (стратегии) Х. Причина этого - несовпадение и относительная противоречивость частных целей, использование для их достижения одних и тех же ограниченных ресурсов (конкуренция).3)Обычный подход - построение компромисса в достижении целей операции; для этого необходимо построить схему компромисса и придерживаться ее при выборе решения.4)Общая постановка проблемы формализуется в виде: найти стратегию (вариант) Х*, отвечающую условиям: 1)стратегия Х* должна быть допустимой (осуществимой, приемлемой); 2)стратегия Х* должна быть наилучшей в смысле принятой схемы компромисса с учетом важности всех локальных критериев (вектора H=(Hq). Пример - конструкция самолета, распределение ресурса между потребителями.
|Eq-Ev|g, q,v{1,2,...,k} 4)принцип справедливой уступки - в форме принципа абсолютной уступки или принципа относительной уступки; основаны на оценке и сопоставлении изменений локальных критериев в области компромисса:
57 Вектор приоритета и вектор весовых коэффициентов (коэффициентов значимости). Сведение многокритериальной задачи к задаче с одним обобщенным критерием. Вектор приоритета задает парные соотн-я критериев по важности: величина Vq определяет, во сколько раз критерий Eq важнее критерия Eq+1; для удобства сопоставления критериев этот ряд показателей чаще всего начинают с 1, т.е. Vk=1; если все критерии равнозначны, то Vq=1 для q=1,2,...,k. Вектор приоритета опр-ся путем попарного сравнения критериев по важности, причем они предварительно упорядочиваются по ряду приоритета I. Вектор весовых коэф-ов H=(H1,H2,...,Hk) представляет собой числовой вектор, его элементы удовлетворяют условиям: 0Hq1, q=1,2,...,k; Hq=1 Компоненты Hq имеют смысл весового коэффициента, задающего важность соответствующего критерия по отношению к остальным критериям (а не попарно, как в случае вектора приоритета). Процедура задания вектора Н значительно сложнее задания вектора V, однако их компоненты связаны соотношениями Vq = Hq/Hq+1, q=1,2,...,k При задании вектора приоритета V его компоненты определяются последовательно, начиная с Vk и достаточно учитывать соотношение важности лишь текущей пары соседних критериев, уже упорядоченных по ряду приоритета. Переход от вектора приоритета к вектору весовых коэффициентов уже не сложен - для этого можно воспользоваться формулой
H3=(V3)/(V1*V2*V3+V2*V3+V3) =(1)/(2*3*1+3*1+1)=0,1
35. Задача ЛП с параметром в функции цели и правых частях ограничений, свойства решающей функции и области разрешимости.
39. Разделы стандартных отчетов прикладного программного обеспечения, отражающие чувствительность решений задач МП.
41 Типовые характеристики развитых прикладных систем для решения задач ЛП и задач ЦП. Сервис офисного программного обеспечения для решения задач МП.
43 Анализ чувствительности и устойчивости решений средствами пакетов прикладного программного обеспечения. Содержание стандартных отчетов.
49 Общая схема прогнозных расчетов и ее содержание. Истолкование места и роли отдельных блоков и этапов прогноза.
55 Способы нормализации критериев. Понятие ряда приоритета. Жесткая и гибкая схемы учета приоритета критериев.
|




 .УСЛОВИЯ:
Хij-искомый
объем поставки;
.УСЛОВИЯ:
Хij-искомый
объем поставки;
 ;
; ;
; Если (2) выполняется,
то ТЗ называется сбалансированной
(закрытой), в противном случае –
несбалансированной (открытой). В
случае, когда суммарные запасы превышают
суммарные потребности, необходим
дополнительный фиктивный (реально не
существующий) пункт потребления,
который будет формально потреблять
существующий излишек запасов, т.е.
Если (2) выполняется,
то ТЗ называется сбалансированной
(закрытой), в противном случае –
несбалансированной (открытой). В
случае, когда суммарные запасы превышают
суммарные потребности, необходим
дополнительный фиктивный (реально не
существующий) пункт потребления,
который будет формально потреблять
существующий излишек запасов, т.е. Если
суммарные
потребности превышают суммарные
запасы,
то необходим дополнительный фиктивный
пункт отправления, формально восполняющий
существующий недостаток продукции в
пунктах отправления:
Если
суммарные
потребности превышают суммарные
запасы,
то необходим дополнительный фиктивный
пункт отправления, формально восполняющий
существующий недостаток продукции в
пунктах отправления:

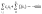 ,αi=<Xi=<βi,i=1,…m-возможный
объем производства у поставщиков.
Среди всех поставщиков
есть действующие и проектируемые.Среди
проектов надо выбрать выгодный,наиболее
эффективный по развитию производства.
Для проектов ограничения
другие:δ6α6=<x6=<δ6β6(для
6-гопроекта),δ-булева
переменная,δ6=1-эффективный,δ6=0-неэффективный.
,αi=<Xi=<βi,i=1,…m-возможный
объем производства у поставщиков.
Среди всех поставщиков
есть действующие и проектируемые.Среди
проектов надо выбрать выгодный,наиболее
эффективный по развитию производства.
Для проектов ограничения
другие:δ6α6=<x6=<δ6β6(для
6-гопроекта),δ-булева
переменная,δ6=1-эффективный,δ6=0-неэффективный.
 ,.
,.
 траектория
Adоптимальная,
переход совершен оптимальным образом
траектория
Adоптимальная,
переход совершен оптимальным образом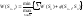 ,Wn=n(Sn-1,Sn)
– шаговый эффект. Задаем Sn-1
и ищем такое Sn
в которое нам эффективней двигаться
и ищем W(Sn-1).
Уравнение Беллмана нужно решать
столько раз, сколько N.
На каждом шаге столько, сколько
состояний.
,Wn=n(Sn-1,Sn)
– шаговый эффект. Задаем Sn-1
и ищем такое Sn
в которое нам эффективней двигаться
и ищем W(Sn-1).
Уравнение Беллмана нужно решать
столько раз, сколько N.
На каждом шаге столько, сколько
состояний. .
. к=1,2,…,n-1,
к=1,2,…,n-1,
 - условно максимальный эффект, зависящий
от
- условно максимальный эффект, зависящий
от



 На этом процесс завершается. Только
на последнем шаге задача разрешима,
т.к. будущее не определено.1)Уравнения
Беллмана все взаимосвязаны 2)Задействованы
все переменные U(U1…Uk…Un)
3)Решение сводится к решению частных
(пошажным).
На этом процесс завершается. Только
на последнем шаге задача разрешима,
т.к. будущее не определено.1)Уравнения
Беллмана все взаимосвязаны 2)Задействованы
все переменные U(U1…Uk…Un)
3)Решение сводится к решению частных
(пошажным).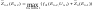

 Перейдя
к первому шагу найдется благоприятное
решение
Перейдя
к первому шагу найдется благоприятное
решение
 - единств. результат. Z1*-
максимальный эффект U1*-
единственное максимальное, таким
способом можно решать любые экономические
задачи. Ограничение – вычислительные
мощности.
- единств. результат. Z1*-
максимальный эффект U1*-
единственное максимальное, таким
способом можно решать любые экономические
задачи. Ограничение – вычислительные
мощности.

 где D - допустимое множество условий;
считая задачу разрешимой, получим
оптимальное решение
где D - допустимое множество условий;
считая задачу разрешимой, получим
оптимальное решение  ,
пусть ему соответствует значение
критерия
,
пусть ему соответствует значение
критерия
 ;
; ,
E1=
,
E1= Пусть
оптимальное значение критерия
Пусть
оптимальное значение критерия 
 ,
E1=
,
E1= ,
E2=
,
E2= Процесс
продолжается либо до исчерпания
списка критериев, либо до тех пор,
когда допустимая область задачи
превратится в точку. Пример схемы
гибкого учета приоритета:
шаг 1:
решается частная задача с функцией
цели - критерием Е1;
по результатам решения формируется
"мягкое" дополнительное
ограничение на значение критерия Е1:
МАХ Е1
------>
E1S1*
Процесс
продолжается либо до исчерпания
списка критериев, либо до тех пор,
когда допустимая область задачи
превратится в точку. Пример схемы
гибкого учета приоритета:
шаг 1:
решается частная задача с функцией
цели - критерием Е1;
по результатам решения формируется
"мягкое" дополнительное
ограничение на значение критерия Е1:
МАХ Е1
------>
E1S1* ,
здесь
E1
-
коэффициент "уступки" (меньший
единицы);
шаг 2:
решается частная задача с функцией
цели - критерием Е2;
по результатам решения формируется
"мягкое" дополнительное ограничение
на значение критерия Е2:
МАХ Е2
------> E2S2*
,
здесь
E1
-
коэффициент "уступки" (меньший
единицы);
шаг 2:
решается частная задача с функцией
цели - критерием Е2;
по результатам решения формируется
"мягкое" дополнительное ограничение
на значение критерия Е2:
МАХ Е2
------> E2S2*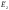 ,
E1S1*
,
E1S1* ,
здесь
S1,S2
- коэффициенты "уступки";
шаг 3:
решается частная задача с функцией
цели - критерием Е3;
по результатам решения формируется
"мягкое" дополнительное
ограничение на значение критерия Е3:
МАХ Е3 ------>
E3S3*
,
здесь
S1,S2
- коэффициенты "уступки";
шаг 3:
решается частная задача с функцией
цели - критерием Е3;
по результатам решения формируется
"мягкое" дополнительное
ограничение на значение критерия Е3:
МАХ Е3 ------>
E3S3* ,
E1S1*
,
E1S1* E2S2*
E2S2* ,
здесь
S1,S2,S3
- коэффициенты "уступки";
процесс
продолжается обычно до исчерпания
списка критериев.
Очевидно,
что процесс формирования коэффициентов
"уступки" S1,S2,...,Sk
не может быть формализован в общем
случае и зависит от оценки
"удовлетворительности" получаемых
значений показателей-критериев
E1,E2,...,Ek;
для такой оценки широко применяются
различные методы и процедуры системного
анализа - методы согласования групповых
решений, экспертные методы и т.п.
Пример - задача определения рациональной
производственной программы предприятия
- критерии минимума затрат на
производство, максимума прибыли
(дохода), минимума затрат на единицу
продукции, минимум затрат дефицитных
ресурсов или привлечения заемных
средств и т.п.
,
здесь
S1,S2,S3
- коэффициенты "уступки";
процесс
продолжается обычно до исчерпания
списка критериев.
Очевидно,
что процесс формирования коэффициентов
"уступки" S1,S2,...,Sk
не может быть формализован в общем
случае и зависит от оценки
"удовлетворительности" получаемых
значений показателей-критериев
E1,E2,...,Ek;
для такой оценки широко применяются
различные методы и процедуры системного
анализа - методы согласования групповых
решений, экспертные методы и т.п.
Пример - задача определения рациональной
производственной программы предприятия
- критерии минимума затрат на
производство, максимума прибыли
(дохода), минимума затрат на единицу
продукции, минимум затрат дефицитных
ресурсов или привлечения заемных
средств и т.п.

 ,
, 12
,
, 12 ,
,
 ,
,
 ,
,
 (максимум
математического ожидания выигрыша)
(максимум
математического ожидания выигрыша) При
анализе игр с природой не имеет смысла
пользоваться смешанными стратегиями,
ибо, в отличие от игр с активным
противником, применение смешанных
стратегий не позволяет увеличить
среднего выигрыша оперирующей стороны.
При
анализе игр с природой не имеет смысла
пользоваться смешанными стратегиями,
ибо, в отличие от игр с активным
противником, применение смешанных
стратегий не позволяет увеличить
среднего выигрыша оперирующей стороны.
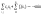 ,αi=<Xi=<βi,i=1,…m-возможный
объем производства у поставщиков.
Среди всех поставщиков
есть действующие и проектируемые.Среди
проектов надо выбрать выгодный,наиболее
эффективный по развитию производства.
Для проектов ограничения
другие:δ6α6=<x6=<δ6β6(для
6-гопроекта),δ-булева
переменная,δ6=1-эффективный,δ6=0-неэффективный.
,αi=<Xi=<βi,i=1,…m-возможный
объем производства у поставщиков.
Среди всех поставщиков
есть действующие и проектируемые.Среди
проектов надо выбрать выгодный,наиболее
эффективный по развитию производства.
Для проектов ограничения
другие:δ6α6=<x6=<δ6β6(для
6-гопроекта),δ-булева
переменная,δ6=1-эффективный,δ6=0-неэффективный.
 ,.
,.
 к началу последнего шага д.б. заранее
предопределено. Решив уравнение для
послед шага мы получим не одно решение,
а множество:
к началу последнего шага д.б. заранее
предопределено. Решив уравнение для
послед шага мы получим не одно решение,
а множество:
 условно максимальные решения для
последнего шага. Для n-1
шага:
условно максимальные решения для
последнего шага. Для n-1
шага:

 и
и
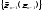













 -
единств результат
-
единств результат максимальный
эффект.
максимальный
эффект. единственное
максимальное (эффективное) управление.
Таким способом можно решать любую
эконом задачу. Отраничение вычеслит.
мощность системы. Любую эконом задачу
можно свести к данной схеме. Известен
зеркальный метод ПРЯМОГО
ХОДА.
единственное
максимальное (эффективное) управление.
Таким способом можно решать любую
эконом задачу. Отраничение вычеслит.
мощность системы. Любую эконом задачу
можно свести к данной схеме. Известен
зеркальный метод ПРЯМОГО
ХОДА. ,
,
 ,
Чтобы
решить, надо оценить, какие возможные
остатки
,
Чтобы
решить, надо оценить, какие возможные
остатки
 следует рассмотреть.
2
шаг: затраты на первых 2-х шагах
следует рассмотреть.
2
шаг: затраты на первых 2-х шагах ,
,
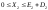 ,k
шаг: условно минимальные затраты
,k
шаг: условно минимальные затраты
 на последнем шаге будет
на последнем шаге будет
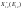 оптимальным и единственным, т.к.
оптимальным и единственным, т.к.
 -фиксирован.
На этом этапе исключаются из рассмотрения
свыше 90% вариантов (неоптимальных).
Можно оценить те потери, которые может
принести отказ от оптимальных.
-фиксирован.
На этом этапе исключаются из рассмотрения
свыше 90% вариантов (неоптимальных).
Можно оценить те потери, которые может
принести отказ от оптимальных.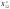 -оптимальное
пополнение в посл
-оптимальное
пополнение в посл
 - с
опред или оптимальным переход остатком,
- с
опред или оптимальным переход остатком,
 -
задана
-
задана
 ;
;
 ;
;
 В
результате получим:
В
результате получим:
 и
и
 ij
– коэф полезного использов, зависит
от технологий и видов топлива.
ij
– коэф полезного использов, зависит
от технологий и видов топлива. - в нем учит-ся
взаимозав-ть видов топлив
- в нем учит-ся
взаимозав-ть видов топлив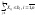 - на перспективу
bi
рассматривается как сценарий
изменяющийся по ресурсам.
- на перспективу
bi
рассматривается как сценарий
изменяющийся по ресурсам. ij
– коэф полезного использов, зависит
от технологий и видов топлива.
ij
– коэф полезного использов, зависит
от технологий и видов топлива. - в нем учит-ся
взаимозав-ть видов топлив
- в нем учит-ся
взаимозав-ть видов топлив - на перспективу
bi
рассматривается как сценарий
изменяющийся по ресурсам.
- на перспективу
bi
рассматривается как сценарий
изменяющийся по ресурсам.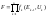 -не
аддитивно.(формула сложного
%-капитализация)
-не
аддитивно.(формула сложного
%-капитализация) .
. 3)принцип
квазиравенства - решение считается
наилучшим, если значения отдельных
критериев отличаются не более чем на
заданную величину g; т.е. получим
множество решений, для которых
3)принцип
квазиравенства - решение считается
наилучшим, если значения отдельных
критериев отличаются не более чем на
заданную величину g; т.е. получим
множество решений, для которых и
и
 5)принцип выделения главного критерия
и задания интервалов по остальным;
6)принцип последовательной оптимизации
и принцип последовательной уступки.
5)принцип выделения главного критерия
и задания интервалов по остальным;
6)принцип последовательной оптимизации
и принцип последовательной уступки. Пример:
Е=(E1,E2,E3),
I={1,2,3}, V=(V1,V2,V3)=(2,3,1) Определим
весовые коэффициенты Hq
вектора H=(H1,H2,H3),
H1=(V1*V2*V3)/(V1*V2*V3+V2*V3+V3)=(2*3*1)/(2*3*1+3*1+1)=0,6
H2=(V2*V3)/(V1*V2*V3+V2*V3+V3)=(3*1)/(2*3*1+3*1+1)=0,3
Пример:
Е=(E1,E2,E3),
I={1,2,3}, V=(V1,V2,V3)=(2,3,1) Определим
весовые коэффициенты Hq
вектора H=(H1,H2,H3),
H1=(V1*V2*V3)/(V1*V2*V3+V2*V3+V3)=(2*3*1)/(2*3*1+3*1+1)=0,6
H2=(V2*V3)/(V1*V2*V3+V2*V3+V3)=(3*1)/(2*3*1+3*1+1)=0,3