
- •Технический университет – упи», 2005
- •Введение Основные понятия
- •Линейные дифференциальные уравнения высшего порядка
- •Решения задания типового варианта
- •4. Решить начальную задачу Коши
- •Ответ: .
- •12. Найти общее решение уравнения
- •V. 17. Последнее задание содержит задачи двух типов – составление и решение дифференциального уравнения на физическую и геометрическую тему. Рассмотрим оба типа задач.
Ответ: .
III. В следующих четырёх номерах даны линейные однородные (11) и неоднородные (12 -15) дифференциальные уравнения второго порядка с постоянными коэффициентами.
11. Найти общие решения дифференциальных уравнений:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение. Для каждого из данных уравнений составляем характеристическое уравнение и решаем его. По виду полученных корней характеристического уравнения (см. формулу (7)) записываем общее решение дифференциального уравнения:
а)
![]() .
.
Его корни
![]() ,
следовательно,
,
следовательно,
![]() ,
тогда фундаментальную систему решений
(ФСР) образуют функции
,
тогда фундаментальную систему решений
(ФСР) образуют функции
![]() .
Поскольку общее решение
.
Поскольку общее решение
![]() является линейной комбинацией произвольных
постоянных и решений ФСР, то для нашего
уравнения общее решение запишется в
виде
является линейной комбинацией произвольных
постоянных и решений ФСР, то для нашего
уравнения общее решение запишется в
виде
![]() ;
;
б)![]() .
.
Его корни
![]() – действительные
равные,
– действительные
равные,
![]() ,
тогда
,
тогда
![]() образуют ФСР и
общее решение
образуют ФСР и
общее решение
![]() исходного уравнения
запишется следующим образом:
исходного уравнения
запишется следующим образом:
![]() ;
;
в)
![]() .
.
Его корни
![]() – действительные
различные, поэтому
– действительные
различные, поэтому
![]() образуют ФСР, и общее решение
образуют ФСР, и общее решение
![]() исходного уравнения запишется следующим
образом:
исходного уравнения запишется следующим
образом:
![]() .
.
Ответ:
а)![]() ;
;
б)
![]() ;
в)
;
в)
![]() .
.
12. Найти общее решение уравнения
![]() .
.
Решение.
Известно, что общее
решение
![]() неоднородного линейного дифференциального
уравнения равно сумме общего решения
неоднородного линейного дифференциального
уравнения равно сумме общего решения
![]() соответствующего
однородного уравнения и некоторого
частного решения
соответствующего
однородного уравнения и некоторого
частного решения
![]() исходного
неоднородного уравнения, т.е.
исходного
неоднородного уравнения, т.е.
![]() .
.
Найдём общее
решение
![]() однородного
уравнения.
однородного
уравнения.
![]() .
Его характеристическое
уравнение
.
Его характеристическое
уравнение
![]() имеет
корни
имеет
корни
![]() ,
т.е.
,
т.е.
![]() ;
тогда
;
тогда
![]() образуют ФСР, и общее решение
образуют ФСР, и общее решение
![]() однородного уравнения запишется
следующим образом:
однородного уравнения запишется
следующим образом:
![]() .
.
Поскольку правая
часть
![]() исходного уравнения является многочленом
второй степени и число
исходного уравнения является многочленом
второй степени и число
![]() не является корнем
характеристического уравнения ОЛДУ,
то частное решение
не является корнем
характеристического уравнения ОЛДУ,
то частное решение
![]() можно искать тоже
в виде многочлена второй степени, но с
неопределёнными коэффициентами.
Значения коэффициентов
А,
В,
и С
нужно искать из условия, что функция
можно искать тоже
в виде многочлена второй степени, но с
неопределёнными коэффициентами.
Значения коэффициентов
А,
В,
и С
нужно искать из условия, что функция
![]() –
решение исходного уравнения. Подставим
эту функцию в заданное уравнение. Удобно
эту подстановку выполнить следующим
образом:
–
решение исходного уравнения. Подставим
эту функцию в заданное уравнение. Удобно
эту подстановку выполнить следующим
образом:
 37
37
![]()
2
![]()
1
![]()

![]() .
.
Приравняв
коэффициенты многочленов при одинаковых
степенях
![]() ,
получим систему трёх уравнений с тремя
неизвестными:
,
получим систему трёх уравнений с тремя
неизвестными:
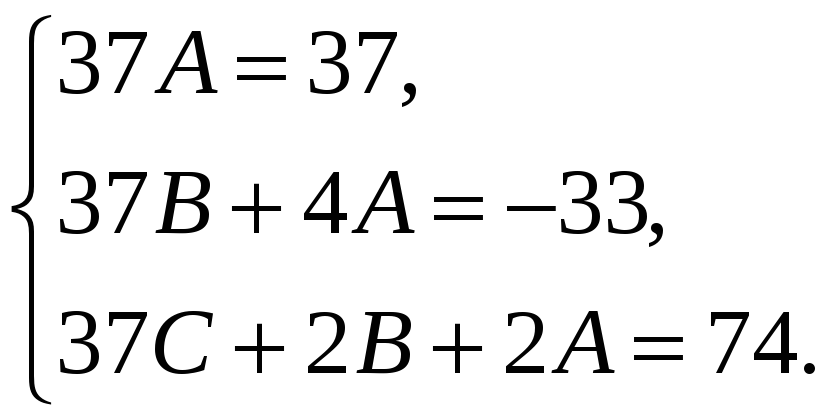
Решив эту систему,
получим, что
![]() .
Тогда
.
Тогда
![]() и
и
![]() – общее решение
исходного уравнения.
– общее решение
исходного уравнения.
Ответ:
![]() .
.
13. Найти общее решение уравнения
![]()
Решение.
Найдём общее
решение
![]() однородного
уравнения
однородного
уравнения
![]() Составим
характеристическое уравнение:
Составим
характеристическое уравнение:
![]() .
Его корни
.
Его корни
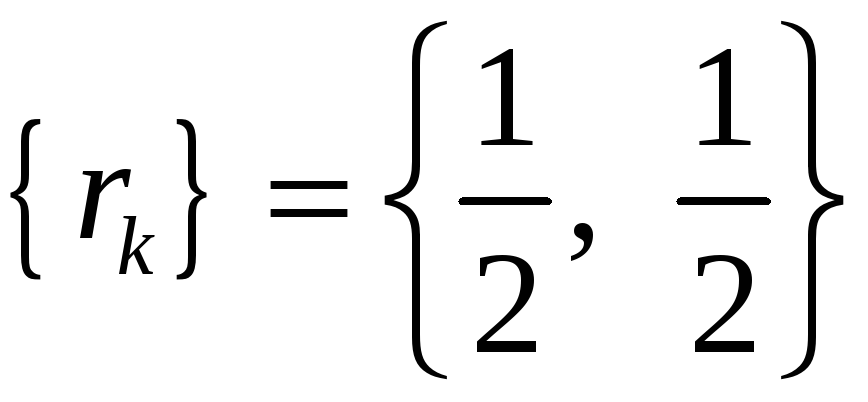 ,
,
![]() ,
тогда
,
тогда
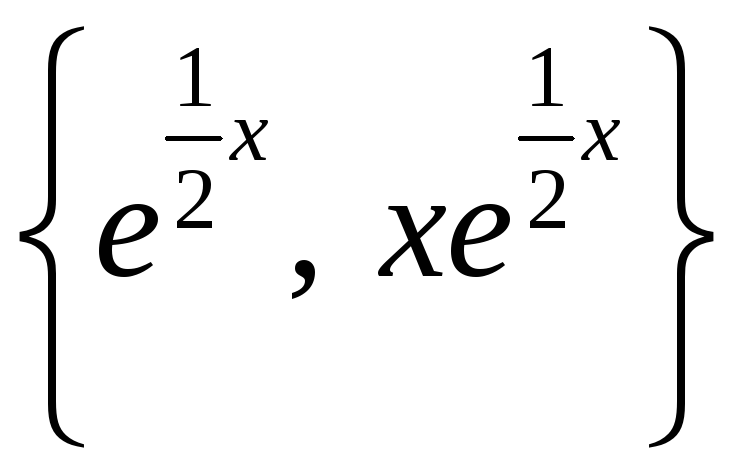 образуют ФСР, и
общее решение
образуют ФСР, и
общее решение
![]() однородного
уравнения запишется следующим образом:
однородного
уравнения запишется следующим образом:
![]() .
.
Поскольку правая
часть данного
уравнения равна
![]() и число
и число
![]() не является корнем характеристического
уравнения ОЛДУ, то согласно формуле
(11) Введения частное решение
не является корнем характеристического
уравнения ОЛДУ, то согласно формуле
(11) Введения частное решение
![]() можно искать в
виде
можно искать в
виде
![]() .
Значения коэффициентов
А
и В
нужно искать из условия, что функция
.
Значения коэффициентов
А
и В
нужно искать из условия, что функция
![]() – решение
исходного уравнения. Подставим эту
функцию в заданное уравнение. Удобно
эту подстановку выполнить следующим
образом:
– решение
исходного уравнения. Подставим эту
функцию в заданное уравнение. Удобно
эту подстановку выполнить следующим
образом:
 1
1
![]()
- 4
![]()
4
![]()

![]() .
.
Приравняв
коэффициенты при функциях
![]() и
и
![]() ,
получим систему двух уравнений с двумя
неизвестными:
,
получим систему двух уравнений с двумя
неизвестными:
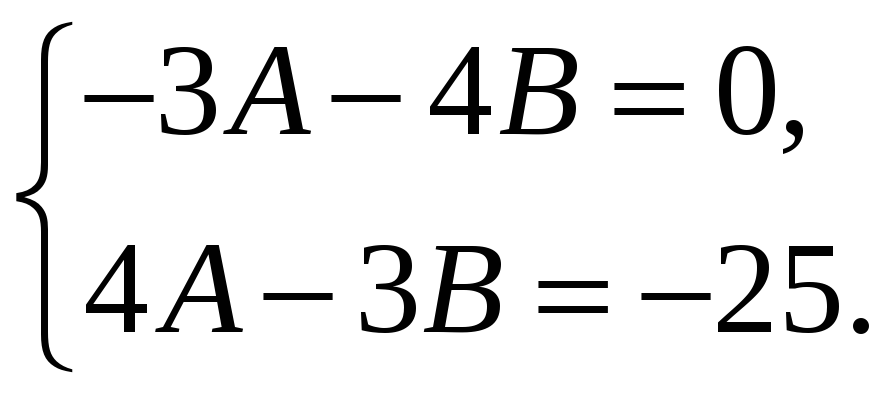
Решив эту систему,
получим, что
![]() .
Тогда
.
Тогда
![]() и
и
![]() – общее решение
исходного уравнения.
– общее решение
исходного уравнения.
Ответ:
![]() .
.
14. Решить задачу Коши для уравнения
![]()
Решение.
Сначала найдём общее решение этого
уравнения. Составим характеристическое
уравнение ОЛДУ:
![]() .
Его корни
.
Его корни
![]() ,
и решение однородного
уравнения запишется в виде
,
и решение однородного
уравнения запишется в виде
![]() . Поскольку правая
часть данного
уравнения равна
. Поскольку правая
часть данного
уравнения равна
![]() и число
и число
![]() является корнем характеристического
уравнения ОЛДУ,
то частное решение
является корнем характеристического
уравнения ОЛДУ,
то частное решение
![]() можно искать в
виде
можно искать в
виде
![]() .
Значение коэффициента
А
нужно искать из условия, что функция
.
Значение коэффициента
А
нужно искать из условия, что функция
![]() –
решение исходного уравнения. Подставим
эту функцию в заданное уравнение. Удобно
эту подстановку выполнить следующим
образом:
–
решение исходного уравнения. Подставим
эту функцию в заданное уравнение. Удобно
эту подстановку выполнить следующим
образом:
-4
![]()
0
![]()
1
![]()


![]() или
или![]() ,
т.е.
,
т.е.
![]() .
Тогда
.
Тогда![]() .
.
Общее решение исходного уравнения запишется следующим образом:
![]() .
.
Для нахождения
частного решения реализуем начальные
условия. Подставив первое условие
![]() ,
получим
,
получим
![]() .
Найдём производную
общего решения
.
Найдём производную
общего решения
![]() и, подставив в неё второе условие
и, подставив в неё второе условие
![]() ,
после упрощения
получим
,
после упрощения
получим
![]() .
Итак, получили
систему двух уравнений с двумя
неизвестными:
.
Итак, получили
систему двух уравнений с двумя
неизвестными:
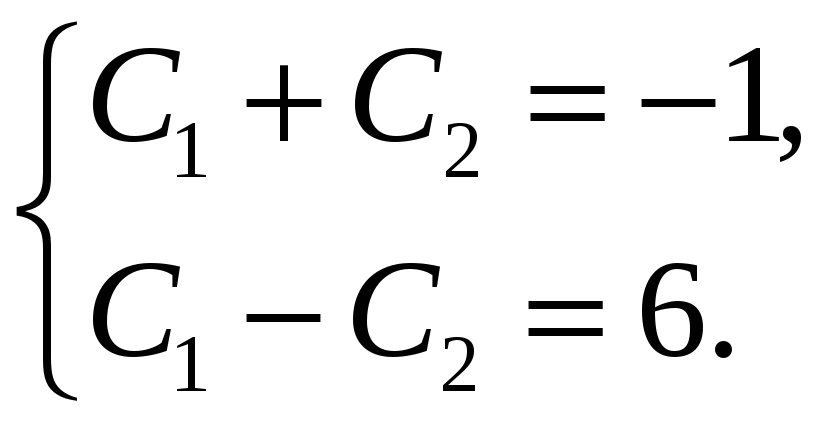
Решением этой
системы является
![]() и
и
![]() ,
тогда решением задачи Коши будет
,
тогда решением задачи Коши будет
![]() .
.
Ответ:
![]() .
.
15. Определить и
записать структуру частного решения
![]() НЛДУ
по виду правой части
НЛДУ
по виду правой части
![]() уравнения
уравнения
![]() :
:
а)
![]() ;
б)
;
б)
![]() .
.
Решение.
а) Запишем характеристическое уравнение
и найдём его корни:
![]() ,
,
![]() .
По условию
.
По условию
![]() ,
тогда
,
тогда
![]() ,
где к
– кратность корня
,
где к
– кратность корня
![]() характеристического уравнения
характеристического уравнения
![]() .
Поскольку
среди корней
характеристического уравнения нет
такого значения, то
.
Поскольку
среди корней
характеристического уравнения нет
такого значения, то
![]() и
и
![]() .
.
б) По
условию
![]() ,
тогда
,
тогда
![]() ,
,
где к
- кратность корня
![]() характеристического уравнения
характеристического уравнения
![]() .
В данном случае снова
.
В данном случае снова
![]() и
и
![]() .
.
Ответ: а)
![]() ;
б)
;
б)
![]() .
.
IV. 16. Решить систему дифференциальных уравнений
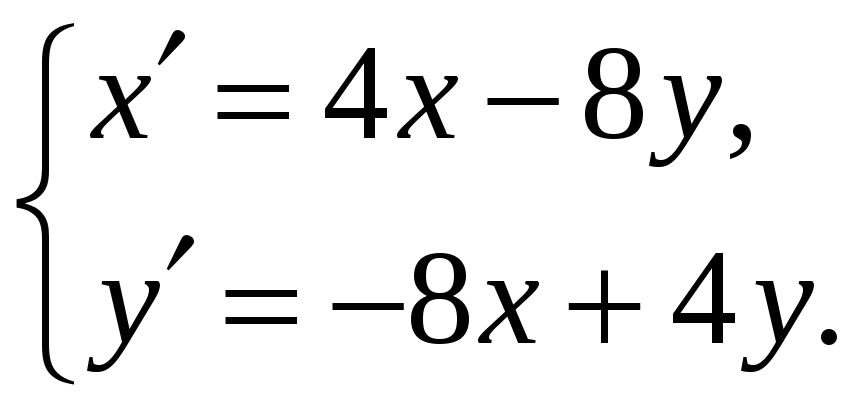
Решение.
Решим систему методом сведения к
однородному дифференциальному уравнению.
Продифференцируем обе части второго
уравнения:
![]() .
Исключив
из этого уравнения
.
Исключив
из этого уравнения
![]() ,
а потом х,
используя сначала первое, а потом второе
уравнения исходной системы, получим
,
а потом х,
используя сначала первое, а потом второе
уравнения исходной системы, получим
![]()
![]() .
.
Итак, получилось
ОЛДУ
второго порядка с постоянными
коэффициентами:
![]() .
Запишем
характеристическое уравнение и найдём
его корни:
.
Запишем
характеристическое уравнение и найдём
его корни:
![]() –
–
![]() ,
тогда
,
тогда
![]() образуют ФСР и
общее решение
образуют ФСР и
общее решение
![]() уравнения запишется следующим образом:
уравнения запишется следующим образом:
![]() .
.
Из второго уравнения
системы получим
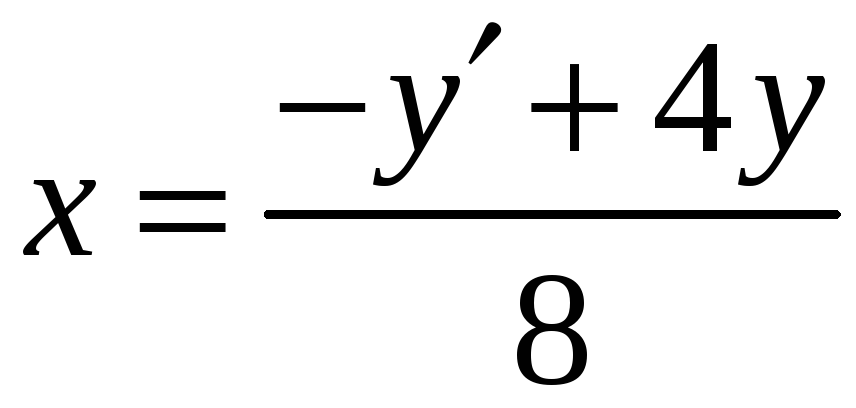 .
Так как
.
Так как
![]() ,
то
,
то
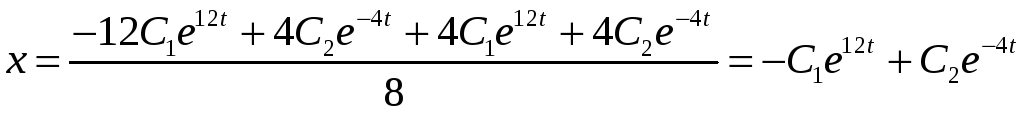 .
.
Итак,
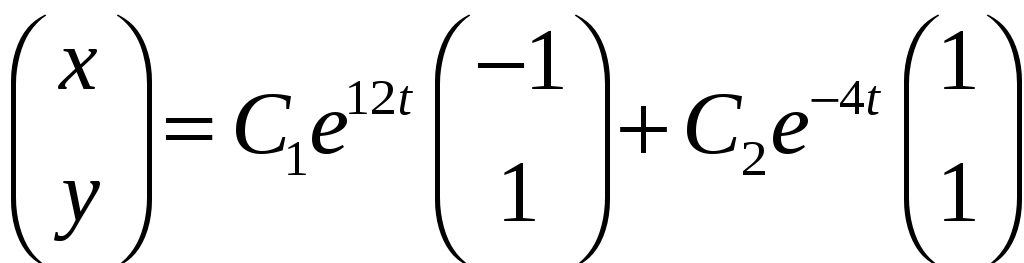 -
общее решение исходной системы.
-
общее решение исходной системы.
Ответ:
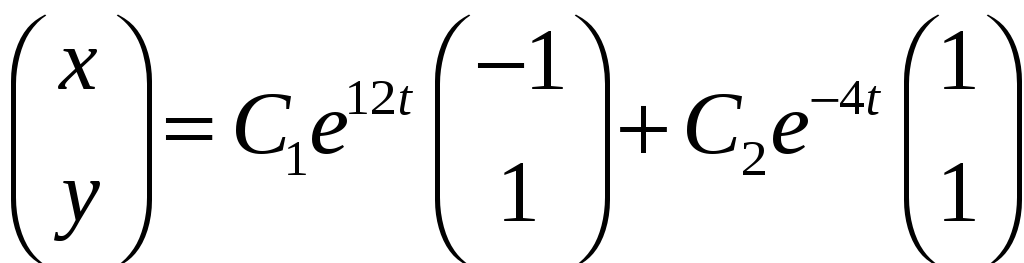 .
.
