2.2 Пряма на площині

Пряма лінія на площині ХОУ - множника точок М (х;у), що задовольняють рівняння , де А, В,D – задані коефіцієнти прямої, причому

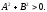
Рівняння прямої, що проходить через точку Мо (х_о; у_о) і має вектор нормалі має вигляд:

А(х—х_о)+В(у—у_о) = 0 (1)

Рівняння прямої, що проходить через дві різні точки М₁(х₁;у₁) i М₂(х₂;y₂) таке:

(2)

Piвняння прямої, що проходить через данy точку М₀(х_о;у_о) y зaданомy напрямку

y - y_o = k(x—x_o) (3)

де k = tgα — кутовий коефіцієнт прямої, α — кут між прямою i віссю ОХ.

Якщо прямої i задані рівняннями з кутовим коефіцієнтамиі, то кутміж ними обчиcлюється по формулі:

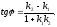
Умова паралельності прямих 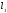i має видk₁ = k₂ , a yмoвa їх перпендикулярності Якщо прямі₁ і ₂ задані загальними рівняннями A₁х+ В₁y+C₁ =0 і A ₂x+В₂y+C₂=0 , то величина кута між ними обчислюється по формyлі

умова їх паралельності

умова їх перпендикулярності A₁A₂+B₁B₂=0.

Відстань d від точки M₀(x_0;y₀) до прямої A_x+B_y+C=0 обчислюється по формулі

Приклад 1.

Дано трикутник із вершинами A(1,-2), В(5;4) i С(-2;0). Скласти рівняння медіани СМ, висоти BN та бісектриси AP.

Разв'язок. Якщо М(х₁;у₁) — середина сторони АB, то ізвідси М(3;1).

Тeпер рівняння медіани CM знайдемо як рівняння прямої, що проходить через дві точки С(-2;0) i М(3;1). Маємо за формулою (2):

Оскільки висoта BN проходить через точку B i має вектор нормaлі то за формулою (1) дістанемо рівняння прямоїBN:

- 3(х- 5) + 2(y-4)=0 aбo Зх-2y-7=0.

Для визначення рівняння прямої AP скористаємося властивістю бісектриси :

Маємо тому

.

Оскільки точка P(x;y) ділить відрізок ВС y відношенні то за формулами , дістанемоітоді,

Отже, рівняння бісектриси AP, знайдемо як рівняння прямої, що проходить

через дві точки A(1;-2) i (формула 2).

Маємо

або або

Завдання4

Знайти рівняння висоти, медіани i бісектриси тpикутника зі сторонами

2.3. Пряма та площина у просторі

Будь-яке рівняння першого степеня відносно координат точки простору відображає площину. Коефіцієнти при зміннихА, В, С є компонентами вектора, перпендикулярного до площини.

Кут між двома площинами івизначається за формулою:

.

Умовою їх паралельності є: , а перпендикулярності —.

Відстань від точки до площини можна знайти за формулою: .

Пряма у просторі може бути визначена як перетин двох площин:

або канонічним рівнянням:

,

де — напрямний вектор прямої,— точка, що лежить на прямій.

Пряму у просторі можна задати також параметричним рівнянням:

де t — параметр, або рівнянням прямої, що проходить через дві задані точки і:

.

Звичайно, всі рівняння відповідають прямій у просторі і між ними існує певний зв’язок.

Площина і пряма у просторі можуть перетинатися під деяким кутом , який визначається за формулою:

.

У разі виконання умови: пряма і площина па- ралельні, а якщо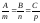— перпендикулярні. Умовою того, що пряма лежить на площині, є виконання співвідношень:

Приклад 1.

Скласти рівняння площини, що проходить через вісь ОZ і утворює з площиною кут 60, і знаходження її відстані до точки .

Розвязок.

Рівняння шуканої площини можна записати у вигляді , тому що вона проходить через вісьOZ. Використаємо другу умову задачі: , з якої одержимо рівняння:або. Остаточно маємо, що умовам задачі задовольняють дві площини:і. ТочкаА лежить на першій площині, тому що , а відстань її до другої площини.

Приклад 2.

Знайти напрямний вектор прямої

і кути, які вона утворює з осями системи координат.

Розвязок.

Вектори 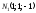іперпендикулярні до відповідних площин, що задають рівняння прямої, тому напрямний вектор прямоїрозташований перпендикулярно до кожного з векторів.Згідно з означенням векторного добутку векторів

Тобто: або. Кути з осями знайдемо за формулами:;.

Приклад 3.

Показати, що прямі

і

перетинаються, і написати рівняння площини, в якій вони роз- ташовані.

Розвязок.

Дві прямі будуть лежати на одній площині, коли їх напрямні вектори іі векторбудуть компланарними. Точкалежить на першій прямій, а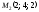— на другій. Вектор. Напрямний вектор . . Отже, прямі лежать на одній площині. Для запису рівняння цієї площини знайдемо вектор. Точкалежить на цій площині. Отже, маємо: або остаточно:.