Завдання 4

Перевірити чи вектори утворюють базис в просторі, якщо «так»,то розкласти вектор по цьому базису.

1. ,

2.

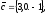
3.

4.

5.

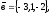
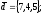
6.

7.

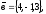
8.

9. ,

10.

11.

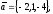
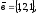
12.

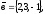
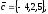
13.

14.

15.

16.

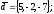
17.

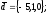
18.

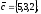
19.

20.

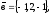
21.

22.

23.

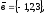
24.

25.

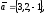
26.

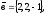
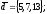
27.

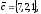
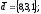
28.

29.

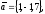
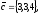
30.

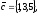
31.

32.

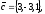
33.

34.

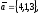
35.

36.

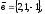
37.

38.

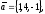
39.

40.

41.

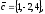
42.

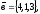
43.

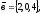
44.

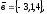
45.

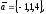
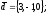
46.

47.

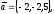
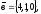
48.

49.

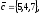
50.

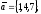
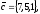
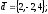
51.

52.

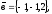
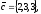
53.

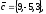
54.

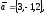
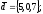
55.

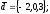
56.

57.

58.

59.

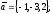
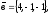
60.

61.

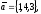
62.

63.

64.

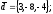
65.

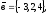
66.

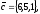
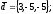
67.

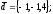
68.

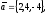
69.

70.

71.

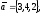
72.

73.

74.

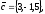
75.

76.

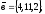
77.

78.

79.

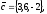
80.

81.

82.

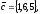
83.

84.

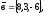
85.

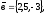
86.

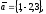
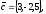
87.

88.

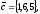
89.

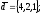
90.

91.

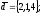
92.

93.

94.

95.

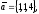
96.

97.

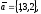
98.

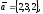
99.

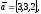
100.

Завдання 5

За даними знайти

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61.

62.

63.

64.

65.

66.

67.

68.

69.

70.

71.

72.

73.

74.

75.

76.

77.

78.

79.

80.

81.

82.

83.

84.

85.

86.

87.

88.

89.

90.

91.

92.

93.

94.

95.

96.

97.

98.

99.

100.

Завдання 6

Знайти рівняння прямої, яка проходить через дві дані точки М₁ і М₂

1. М₁ (1,3), М₂ (2,-1); 2. М₁ (-1,2), М₂ (2,2); 3. М₁ (-3,1), М₂ (1,1);

4. М₁ (-2,1), М₂ (2,1); 5. М₁ (-2,2), М₂ (1,0); 6. М₁ (1,-2), М₂ (3,4);

7. М₁ (2,-3), М₂ (0,-2); 8. М₁ (4,-3), М₂ (1,3); 9. М₁ (5,1), М₂ (-3,4);

10. М₁ (1,3), М₂ (2,-1); 11.М₁ (2,-3), М₂ (-2,-1); 12. М₁ (1,-1), М₂ (-3,1);

13. М₁ (3,4), М₂ (4,-3); 14. М₁ (3,-4), М₂ (2,-3); 15. М₁ (2,-3), М₂ (2,-4);

16. М₁ (3,-6), М₂ (4,-5); 17. М₁ (3,-7), М₂ (2,-3); 18. М₁ (2,-5), М₂ (1,3);

19. М₁ (1,3), М₂ (2,-3); 20. М₁ (1,-3), М₂ (3,-2); 21. М₁ (2,-4), М₂ (-1,3);

22. М₁ (-1,-6), М₂ (-4,-3); 23. М₁ (-4,1), М₂ (2,-3); 24. М₁ (-3,-5), М₂ (1,3);

25. М₁ (3,2), М₂ (2,-3); 26. М₁ (9,11), М₂ (-7,0); 27. М₁ (2,3), М₂ (3,-1);

28. М₁ (1,2), М₂ (3,4); 29. М₁ (8,2), М₂ (2,-3); 30. М₁ (4,5), М₂ (3,3);

31. М₁ (0,2), М₂ (6,-4); 32.М₁ (-2,4), М₂ (8,-7); 33. М₁ (-4,2), М₂ (-1,4);

34. М₁ (6,-1), М₂ (2,0); 35.М₁ (1,8), М₂ (-5,3); 36. М₁ (9,8), М₂ (7,6);

37. М₁ (3,1), М₂ (1,4); 38. їМ₁ (2,3), М₂ (0,-2); 39. М₁ (1,7), М₂ (-1,4);

40. М₁ (-3,1), М₂ (2,3); 41. М₁ (1,1), М₂ (-3,2); 42. М₁ (-1,3), М₂ (-4,2);

43. М₁ (4,-2), М₂ (1,8); 44. М₁ (2,3), М₂ (1,2); 45. М₁ (6,0), М₂ (-2,3);

46. М₁ (6,5), М₂ (-2,4); 47. М₁ (1,3), М₂ (2,2); 48. М₁ (-2,1), М₂ (1,8);

49. М₁ (3,2), М₂ (-2,1); 50. М₁ (2,2), М₂ (4,5); 51. М₁ (3,4), М₂ (-2,4);

52. М₁ (4,2), М₂ (1,-3); 53. М₁ (1,-4), М₂ (-1,2); 54. М₁ (2,4), М₂ (7,-9);

55. М₁ (-2,1), М₂ (4,6); 56. М₁ (3,6), М₂ (1,9); 57. М₁ (5,-7), М₂ (8,11);

58. М₁ (3,2), М₂ (-6,5); 59. М₁ (2,3), М₂ (4,2); 60. М₁ (1,9), М₂ (-4,1);

61. М₁ (-1,2), М₂ (4,2); 62. М₁ (3,1), М₂ (2,-3); 63. М₁ (1,2), М₂ (5,1);

64. М₁ (-4,5), М₂ (6,-2); 65. М₁ (2,-3), М₂ (1,6); 66. М₁ (1,7), М₂ (0,2);

67. М₁ (11,5), М₂ (-7,6); 68. М₁ (2,-2), М₂ (1,-4); 69. М₁ (5,3), М₂ (1,-4);

70. М₁ (-12,6), М₂ (7,5); 71. М₁ (5,3), М₂ (2,1); 72. М₁ (-1,3), М₂ (4,9);

73. М₁ (2,-6), М₂ (4,2); 74. М₁ (4,1), М₂ (-2,3); 75. М₁ (6,5), М₂ (2,5);

76. М₁ (-2,5), М₂ (4,-3); 77. М₁ (-3,1), М₂ (2,5); 78. М₁ (1,2), М₂ (3,4);

79. М₁ (4,-5), М₂ (3,-4); 80. М₁ (8,0), М₂ (1,1); 81. М₁ (5,7), М₂ (-1,-1);

82. М₁ (3,8), М₂ (7,-3); 83. М₁ (3,-1), М₂ (1,-3); 84. М₁ (8,-9), М₂ (1,0);

85. М₁ (2,-3), М₂ (1,6); 86. М₁ (6,-2), М₂ (2,8); 87. М₁ (4,1), М₂ (2,-5);

88. М₁ (5,1), М₂ (-2,3); 89. М₁ (0,-1), М₂ (1,-6); 90. М₁ (1,1), М₂ (7,4);

91. М₁ (-4,2), М₂ (2,-1); 92. М₁ (3,1), М₂ (1,2); 93. М₁ (-9,5), М₂ (0,2);

94. М₁ (2,3), М₂ (-1,4); 95. М₁ (5,7), М₂ (7,0); 96. М₁ (3,7), М₂ (2,1);

97. М₁ (0,3), М₂ (-1,-1); 98. М₁ (-3,2), М₂ (4,-1); 99. М₁ (-1,-3), М₂ (2,0);

100. М₁ (1,-4), М₂ (1,6).