
150_Начерт. геометрия_контрольная для БТИ
.pdf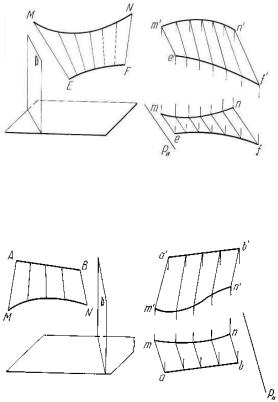
К числу линейчатых развертывающихся поверхностей относятся также поверхности с ребром возврата. Они образуются перемещением прямой линии по некоторой пространственной кривой, причем образующая прямая остается все время касательной к направляющей (рисунок 45а). При продлении касательных в противоположную сторону от точек касания (точек 1, 2, 3, 4, 5) будет образована вторая полость поверхности. Границей же между первой и второй полостями будет являться направляющая кривая MN , называемая ребром возврата. Эпюр некоторой поверхности с ребром возврата приведен на рисунке 45б.
Из линейчатых неразвертывающихся поверхностей следует в первую очередь отметить цилиндроиды — поверхности, образуемые движением прямой, скользящей по двум кривым направляющим, не лежащим в одной плоскости, и остающейся все время параллельной некоторой заданной плоскости (Р), называемой плоскостью параллелизма (рисунок 46а). Эпюр цилиндроида приведен на рисунке 46б.
а |
б |
Рисунок 46
Если одной из направляющих цилиндроида является прямая линия, образуется новая линейчатая неразвертывающаяся поверхность, называемая
коноидом (рисунок 47).
Рисунок 47
31
Если же обе направляющие цилиндроида заменить прямыми линиями (скрещивающимися), то образуется линейчатая неразвертывающаяся поверхность — косая плоскость, или линейчатый параболоид, или гиперболический параболоид (рисунок 48).
Рисунок 48
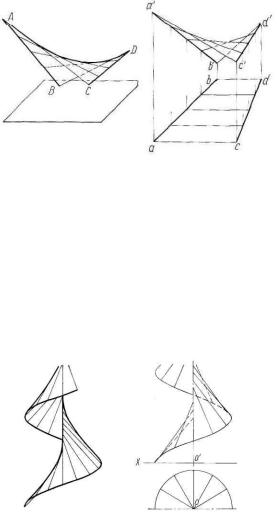
Большую группу линейчатых неразвертывающихся поверхностей составляют винтовые поверхности (гелисоиды), имеющие широкое применение в технике. Винтовые поверхности — это такие поверхности, у которых хотя бы одна направляющая — винтовая линия.
Если прямая линия (образующая) перемещается в пространстве, пересекая винтовую линию и ее ось (направляющие), причем угол между нею и осью винтовой линии остается постоянным и неравным 90°, образуется поверхность, называемаякосым гелисоидом (рисунок 49).
В этом случае, когда угол между образующей косого гелисоида и осью винтовой линии постоянен и равен 90°, получается прямой гелисоид, или винтовой коноид.
Рисунок 49
На рисунке 50 показана поверхность, называемая косым кольцевым гелисоидом. Она образуется прямой линией, которая, перемещаясь в пространстве, пересекает две соосные винтовые линии одинакового шага. Причем
32
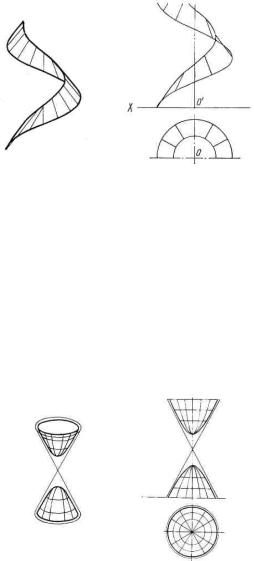
угол между образующей и осью винтовых линий должен быть постоянным и не равным 90°.
Рисунок 50
Если же этот угол постоянен и не равен 90°, поверхность называется вин-
товым цилиндроидом.
К нелинейчатым относится также большая группа поверхностей, которые могут быть получены вращением некоторой кривой линии вокруг неподвижной прямой — оси поверхности, т. е. поверхностей вращения. К поверхностям вращения могут быть отнесены также рассмотренные ранее прямой круговой цилиндр и прямой круговой конус. Но это поверхности вращения с прямолинейными образующими, т. е. линейчатые поверхности вращения.
При образовании поверхностей вращения каждая точка их образующих перемещается по окружности, перпендикулярной к оси вращения. Эти окружности называются параллелями, а наибольшая из них — экватором. Осевая плоскость называется меридиональной, а линия ее пересечения с поверхностью — меридианом.
Рисунок 51
Из поверхностей вращения дадим определение следующим. Сферическая поверхность (шар) — это поверхность, образуемая враще-
нием окружности вокруг ее диаметра.
33
Эллипсоид вращения — это поверхность, образуемая вращением эллипса вокруг его большой (вытянутый эллипсоид вращения) или малой (сжатый эллипсоид вращения) оси.
Двухполостной гиперболоид вращения (рисунок 51) — поверхность, обра-
зуемая вращением гиперболы вокруг ее действительной оси.
Рисунок 52
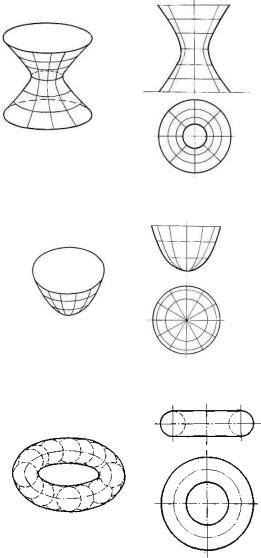
Однополостной гиперболоид вращения (рисунок 52) — поверхность, об-
разуемая вращением гиперболы вокруг ее мнимой оси.
Рисунок 53
Параболоид вращения (рисунок 53) — поверхность, образуемая вращением параболы вокруг ее оси.
Рисунок 54
34

Тор (круговое кольцо) — поверхность, образуемая вращением окружности вокруг оси, лежащей с ней в одной плоскости и ее не пересекающей (рисунок 54).В общем виде торовая поверхность — это поверхность, образуемая вращением окружности (или ее дуги) вокруг оси, расположенной с нею в одной плоскости, но не проходящей через ее центр.
Боковая поверхность прямого кругового цилиндра получается вращением отрезка АВ (образующей) вокруг оси, параллельной этому отрезку (рисунок 55). Окружность по которой осуществляется вращение называется направляющей. В данном случае направляющая совпадает с окружностью очерка основания цилиндра.
Рисунок 55
Построение сечения прямого кругового цилиндра аналогично построению сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра.
Если в задании указана необходимость построения развертки, то целесообразно горизонтальную проекцию основания разделить на равные части и с помощью линий связи построить фронтальные проекции образующих цилиндра (рисунок 56).
Действительный вид фигуры сечения получен на рисунке 56 способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой.
Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения показана на рисунке 57.
Для построения развертки на горизонтальной прямой откладывают длину окружности основания, взятую с горизонтальной проекции цилиндра с помощью циркуля. Из точек деления восставляют перпендикуляры и на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости, которые берут с фронтальной или профильной проекции цилиндра. Полученные точки 10...90, соединяют по лекалу плавной кривой. Затем пристраиваем фигуру сечения с частью верхнего основания цилиндра и нижнее основание цилиндра.
35

Рисунок 56
Рисунок 57
36
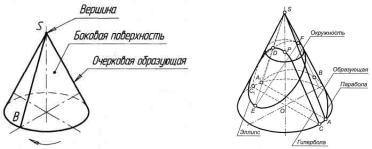
Наглядное изображение прямого кругового конуса показано на рисунке 58а. Боковая поверхность конуса получается при вращении отрезка BS вокруг оси конуса по направляющей — окружности основания.
а |
б |
Рисунок 58
В зависимости от расположения секущей плоскости по отношению к оси прямого кругового конуса получаются различные фигуры сечения, ограниченные кривыми линиями (рисунок 58б).
Сечение прямого кругового конуса фронтально-проецирующей плоскостью рассматривается на рисунке 59.
Для построения горизонтальной проекции фигуры сечения горизонтальную проекцию основания конуса (окружность) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях проводят вспомогательные образующие. Сначала находят фронтальные проекции точек сечения 1"—12", лежащих на секущей плоскости. Затем с помощью линий связи находят их горизонтальные проекции. Найденные горизонтальныепроекцииточек контура сечения соединяют.
Действительный вид фигуры сечения в данном примере найден способом перемены плоскости проекций.
Построение развертки поверхности конуса (рисунок 60) начинают с проведения дуги окружности радиусом, равным длине образующей конуса из точки S0. Длину дуги можно определить как по формуле, так и аналогично нахождению длины боковой поверхности цилиндра.
Точки, перенесенные на дугу соединяют с вершиной S0. От основания откладывают действительные длины отрезков образующих.
Действительные длины этих отрезков находят, как и в примере с пирамидой, способом вращения около вертикальной оси, проходящей через вершину конуса.
К развертке конической поверхности пристраивают фигуры сечения и основания конуса.
37
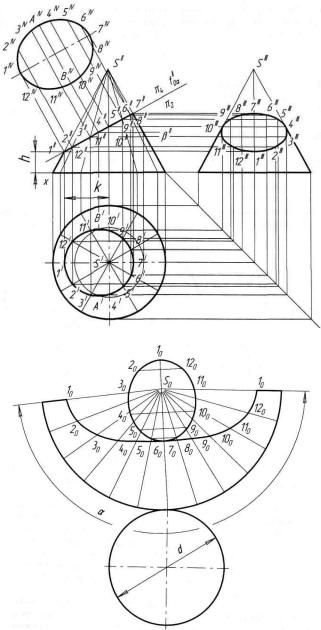
Рисунок 59
Рисунок 60
38
ТЕМА 5 Касательные линии и плоскости к поверхности
При решении некоторых задач (например, построение теней, нахождение характерных точек линии пересечения поверхностей) приходится строить плоскости, касательные к кривым поверхностям.
Плоскость, касательная к поверхности в данной точке, — это плоскость,
которая содержит прямые, касательные ко всем кривым, лежащим на заданной поверхности и проходящим через данную точку. Следовательно, в общем случае для построения такой плоскости достаточно провести две пересекающиеся прямые, каждая из которых является касательной к любой кривой линии, принадлежащей заданной поверхности и проходящей через точку касания. В некоторых же конкретных случаях задача может решаться еще проще.
Следует иметь в виду, однако, что плоскость, касательная к кривой поверхности, в зависимости от вида этой поверхности может касаться ее не только в одной точке, по и иметь общую прямую или кривую линию, а затем и пересекать эту поверхность. Так, плоскость, касательная к сферической поверхности, имеет с ней только одну общую точку; плоскость, касательная к коническойповерхности, — прямуюлинию и т. д.
Прямая, перпендикулярная к касательной плоскости в точке касания, на-
зывается нормалью данной поверхности в данной точке.
ТЕМА 6 Аксонометрические проекции
На практике весьма часто возникает необходимость в наглядном изображении предмета на чертеже, т. е. в изображении его в трех измерениях. Это достигается аксонометрическими проекциями, сущность которых заключается в том, что изображаемый предмет располагается по отношению к некоторой плоскости проекций так, что при параллельном проецировании на нее ни одна из осей координат, к которым он отнесен в пространстве, не проецируется на плоскость проекций в виде точки. В результате ни одно из измерений изображаемого предмета не исчезает, и он проецируется на плоскость проекции в трех измерениях, а не в двух, как это получается при прямоугольном параллельном проецировании на три взаимно перпендикулярные плоскости проекций.
Размеры изображаемого предмета при аксонометрическом проецировании по всем трем осям искажаются.
В зависимости от расположения плоскости проекций и направления проецирования возможны случаи, когда показатели искажения по всем трем осям одинаковы, или равны между собой только по двум осям, или показатели искажения по всем трем осям не равны между собой. Соответственно этому аксонометрические проекции называют изометрическими (износ — одинаковый), диметрическими (ди— двойной) и триметрическими.
39
Аксонометрические проекции бывают также прямоугольные (когда направление проецирования составляет с плоскостью проекций прямой угол)
икосоугольные.
Вмашиностроении принято использовать прямоугольное проецирование. Для прямоугольного проецирования: к2 + т2 + п2=2.
Кроме этого, сумма квадратов двух любых показателей искажения не может быть меньше единицы.
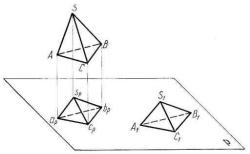
Основной теоремой аксонометрии является теорема Польке — Шварца, которая утверждает, что проекцией произвольного тетраэдра (треугольной пирамиды) может служить любой четырехугольник вместе с его диагоналями (рисунок 61).
Рисунок 61
На рисунке 61 показан произвольный тетраэдр SABC в пространстве, Р
— плоскость проекций; S1A1B1C1 — изображение произвольного, четырехугольника с диагоналями. К. Польке и Г. Шварц доказали, что всегда можно найти такое положение тетраэдра в пространстве и такое направление проецирования, при которых проекция тетраэдра на плоскость Р будет, иметь вид четырехугольника spapbpсp, подобного произвольно изображенному S1A1B1C1. Отсюда вывод, что любые три прямые линии, расположенные в одной плоскости и проходящие через одну точку, могут быть приняты за аксонометрические оси и на них могут быть выбраны любые показатели искажения, лишь бы сумма их квадратов не была меньше двух, а сумма квадратов двух любых из них не была меньше единицы.
Но на практике применяются только некоторые определенные направления аксонометрических осей и определенные величины показателей искажения.
Прямоугольная изометрическая проекция. При равном наклоне аксоно-
метрической плоскости проекций ко всем трем осям координат и прямоугольном проецировании эта система спроецируется на плоскость проекций так, как показано на рисунке 62а. Показатели искажения в этом случае по всем трем осям оказываются одинаковыми иравными 0, 82. Это прямоуголь-
ная изометрическая проекция. Но для упрощения построений на практике применяют так называемые приведенные показатели искажения, равные
40
