Гидралика грутновых вод (Фильтрация)

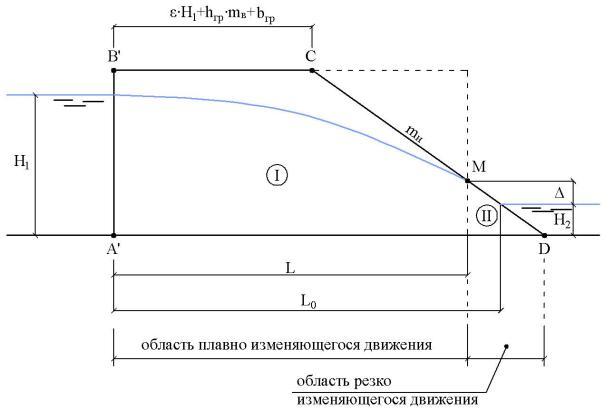
щимся характером движения грунтовых вод и установить величину промежутка высачивания .

Рис. 11.19. Условный продольный профиль плотины с вертикальным верховым откосом.

Одним из характерных размеров условного профиля является L0 – расстояние по горизонтали между верховым вертикальным откосом и точкой пересечения низового откоса с линией уровня воды в нижнем бьефе. Величина L0 может быть снята с чертежа условного профиля, или определена на основании геометрических соотношений:

L0 = bгр + ε × H1 + mн × (Hпл - H2 ) ,

где H пл – высота плотины.

Таким образом, L0 – заранее известная величина.

31

В соответствии с характером движения фильтрационного потока условный профиль A’B’CD можно рассматривать состоящим из двух фрагментов (фрагменты показаны на Рис. 11.18 римскими цифрами I и II).

Фрагмент I – область плавно изменяющегося движения.

Фрагмент II – область резко изменяющегося движения, соответствующая промежутку высачивания .

Из неразрывности потока внутри тела плотины следует, что величина удельного фильтрационного расхода q в этих фрагментах одинакова:

q = qI = qII

где qI – фильтрационный расход, проходящий через первый фрагмент условного профиля;

qII – фильтрационный расход, проходящий через второй фрагмент условного профиля;

Напишем уравнения для определения величины q для каждого из фрагментов условного профиля, рассматривая их по отдельности.

∙ Фрагмент I.

Рис. 11.20. Фрагмент I условного продольного профиля (область плавно изменяющегося движения).

32

Поскольку движение фильтрационного потока в первом фрагменте плавно изменяющееся, для определения величины удельного фильтрационного расхода q можно использовать уравнение Дюпюи (11.3).

Запишем уравнение Дюпюи для рассматриваемого фрагмента I, учитывая, что глубина потока в верхнем бьефе равна H1 , а в нижнем бьефе –

вестной является расстояние L, характеризующее длину области с плавно изменяющимся движением.

Уменьшим число неизвестных, входящих в выражение (11.5), выразив L через известную величину L0 :

L = L0 - mн × D

Тогда выражение (11.5) для удельного расхода первого фрагмента примет вид:

· Фрагмент II (низовой клин).

33

Рис. 11.21. Фрагмент II условного продольного профиля (область резко изменяющегося движения).

Для определения величины удельного фильтрационного расхода qII во втором фрагменте условного профиля A’B’CD использовать уравнение Дюпюи нельзя, так как движение фильтрационного потока резко изменяющееся. Поэтому q определяют, используя формулу Дарси, разбивая рассматриваемый фрагмент на две зоны горизонтальным сечением 1-1 (см. Рис. 11.21).

∙ Верхняя зона, соответствующая промежутку высачивания . Через эту зону проходит фильтрационный расход q1 , причём фильтрационный поток выходит из тела плотины в атмосферу.

∙ Нижняя зона, находящаяся ниже уровня воды в нижнем бьефе. Через эту зону проходит фильтрационный расход q2 , причём фильтрационный поток выходит под уровень нижнего бьефа.

Искомая величина фильтрационного расхода через фрагмент II будет суммой расходов через верхнюю и нижнюю зоны:

qII = q1 + q2

Верхняя зона.

34

Определим величину расхода q1 для верхней зоны. Для этого составим дифференциальное уравнение, описывающее движение фильтрационного потока в этой зоне.

Для составления дифференциального уравнения проведём вертикальную координатную ось OY (см. Рис. 11.21), начало координат которой соответствует точке M (точке выхода кривой депрессии на низовой откос).

Выделим в пределах верхней зоны элементарную струйку высотой dy, несущую удельный расход dq1 . Длина этой элементарной струйки:

ходящего через верхнюю зону фрагмента II.

35

q = K × D

1 mн

Нижняя зона.

Подобным образом определим расход q2 для нижней зоны. Для этого также составим дифференциальное уравнение, выделяя элементарную струйку в пределах нижней зоны фрагмента II. Длина такой струйки также равна:

,

Для любой струйки, находящейся под уровнем воды в нижнем бьефе, то есть как раз в пределах нижней зоны, характерно то, что фильтрация происходит под действием напора, равного величине промежутка высачивания . То есть потери в каждой элементарной струйке нижней зоны равны:

hl = D

(фильтрация происходит за счёт того, что срабатывается действующий напор ).

Пьезометрический уклон для рассматриваемой струйки:

I= hll = y × mн

Исогласно формуле Дарси, скорость фильтрации и величина фильтрационного расхода для рассматриваемой элементарной струйки:

V = K × I = K × mн × y

dq = V × dy = K × mн × y × dy

Для определения величины удельного фильтрационного расхода, проходящего через низовую зону фрагмента II, проинтегрируем получен-

36

Таким образом, величина удельного расхода для всего фрагмента II:

Итак, теперь имеются выражения для определения величин удельного фильтрационного расхода qI и qII в каждом из рассматриваемых фрагментов условного профиля плотины. В каждое из этих выражений входит неизвестная величина промежутка высачивания .

Для определения величин q и необходимо решить систему уравнений для условного профиля плотины A’B’CD. Эта система уравнений состоит из уравнений (11.6) и (11.7) для величины удельного фильтрационного расхода в каждом из рассматриваемых фрагментов условного профиля:

37

или, исключая первое выражение системы уравнений:

Эту систему уравнений удобно решать графически, выполняя построение двух графиков qI = f ( ) и qII = f ( ) для фрагментов I и II. Точка

Построение кривой депрессии выполняется также как и в случае прямоугольного массива грунта по выражению (11.6). В нижнем бьефе глубина фильтрационного потока равна H2 + .

Для построения кривой депрессии снова рассмотрим условный профиль плотины A’B’CD с вертикальным верховым откосом. Очевидно, что кривая депрессии находится в пределах фрагмента I. Наметим в пределах этого фрагмента два вертикальных живых сечения 1-1 и 2-2. Сечение 2-2 находится в точке M выхода кривой депрессии на низовой откос плотины, глубина фильтрационного потока в этом сечении известна и равна H2 + . Сечение 1-1 располагается на произвольном расстоянии x от сечения 2-2, отсчитываемом в сторону верхнего бьефа. Глубина h в сечении 1-1 является искомой величиной, которую можно определить из уравнения Дюпюи, которым соединяются сечения 1-1 и 2-2:

38

q = h2 - (H2 + D)2 ,

2 × x

откуда

Рис. 11.22. К построению кривой депрессии для условного профиля A’B’CD.

Располагая сечение 1-1 на разных расстояниях x от сечения 2-2 по выражению (11.8) получаем таблицу координат кривой депрессии, относительно точки M рассматриваемого условного профиля. По данным такой таблицы может быть выполнен чертёж кривой депрессии для условного профиля A’B’CD.

39

Рис. 11.23. К построению кривой депрессии для действительного профиля ABCD.

Для построения кривой депрессии в пределах действительного профиля ABCD выполняют следующие действия (см Рис.11.23):

Кривая депрессии, построенная для условного профиля A’B’CD переносится на действительный профиль ABCD.

В результате переноса кривой депрессии на действительный профиль точка k пересечения поверхности воды в верхнем бьефе и верхового откоса действительного профиля оказывается выше кривой депрессии. Для сопряжения построенной ранее кривой депрессии (перенесённой на дей-

40