Основные краевые задачи для уравнений Пуассона и Лапласа

Перечислим основные краевые задачи, связанные с уравнениями Пуассона и Лапласа, и их вариационные формулировки.

Первая краевая задача или задача Дирихле для уравнения Пуассона состоит в отыскании непрерывной функции, удовлетворяющей уравнению Пуассона

, (14)

и краевому условию

(15)

на границе S области Ω. Здесь Ω — некоторая конечная m-мерная область (можно считать m = 2 или m =3). Областью определения оператора Лапласа является линейное множество функций, которые непрерывны вместе со своими первыми и вторыми производными в замкнутой области и которые равны нулю наS.

Сформулированная задача Дирихле равносильна задаче о минимуме функционала

. (16)

Вторая краевая задача или задача Неймана для уравнения Пуассона состоит в отыскании непрерывной функции, удовлетворяющей уравнению Пуассона (14) и краевому условию

(17)

на границе S области Ω (n — внешняя нормаль к поверхности S). Здесь областью определения оператора Лапласа является линейное множество функций, которые непрерывны вместе со своими первыми и вторыми производными в замкнутой области ; удовлетворяют краевому условию (17) и удовлетворяют условию

. (18)

Условие (18) необходимо для единственности решения. Отметим, что для разрешимости задачи Неймана необходимо, чтобы

. (19)

Сформулированная задача Неймана равносильна задаче о минимуме функционала (16).

Краевое условие (17) — естественное, поэтому нет нужды ему удовлетворять заранее, отыскивая минимум функционала (16).

Третья краевая задача для уравнения Пуассона состоит в отыскании непрерывной функции, удовлетворяющей уравнению Пуассона (14) и краевому условию

(20)

на границе S области Ω. Здесь областью определения оператора Лапласа является линейное множество функций, которые непрерывны вместе со своими первыми и вторыми производными в замкнутой области и которые удовлетворяют краевому условию (20).

Сформулированная третья краевая задача равносильна задаче о минимуме функционала

. (21)

Краевое условие (20) – естественное.

Часто приходится решать уравнение Лапласа с сопутствующим ему неоднородным краевым условием. Приведем формулировки основных задач в этом случае.

Интегрирование уравнения Лапласа в области Ω при краевом условии (задача Дирихле)

(22)

приводит к отысканию минимума функционала

(23)

на множестве функций, удовлетворяющих условию (22); если краевое условие имеет вид (задача Неймана)

, (24)

то задача сводится к отысканию минимума функционала

(25)

на множестве функций, которые никаким краевым условиям не подчинены. Добавим к этому, что в случае краевого условия смешанного типа (третья краевая задача)

, (26)

соответствующий функционал имеет вид

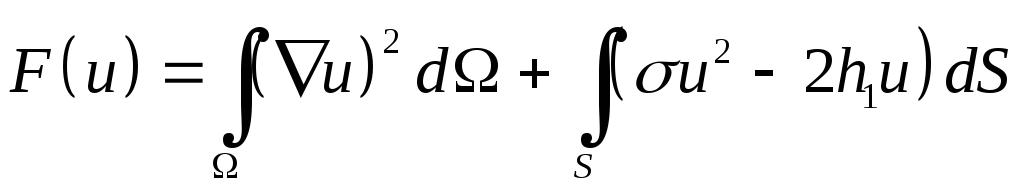. (27)

Метод Бубнова–Галеркина

Метод Бубнова–Галеркина можно рассматривать как обобщение метода Ритца для уравнений вида (6), где оператор А не обязательно положительный.

Пусть неизвестная функция u(P) удовлетворяет в некоторой области Ω неоднородному уравнению

(28)

и, может быть, некоторым однородным граничным условиям.

Выберем бесконечную последовательность координатных функций φ₁, φ₂, …, φ_n, …, которые достаточное число раз (в соответствии с данными задачи) непрерывно дифференцируемы в замкнутой области и которые удовлетворяют всем краевым условиям нашей задачи. Как обычно, черезS обозначена граница области Ω.

Будем считать, что как уравнение (28), так и соответствующие ему краевые условия — линейные, тогда функция (10) удовлетворяет всем краевым условиям.

По методу Бубнова–Галеркина коэффициенты a_j определяются из требования, чтобы левая часть уравнения (28) стала, после подстановки в нее u_n(P) вместо u(P), ортогональной к функциям φ₁, φ₂, …, φ_n.

Метод Бубнова–Галеркина тем самым приводит к системе линейных алгебраических уравнений, которая по виду тождественна с системой (13) метода Ритца. Отсюда нетрудно заключить, что методы Бубнова–Галеркина и Ритца совпадают, если оператор А положительно определенный. В общем же случае метод Ритца неприменим, тогда как метод Бубнова–Галеркина сохраняет силу.