
C2-2011
.pdf
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
4.3. Координатный метод
Координатный метод является естественным продолжением векторного метода, то есть вектор пространства есть упорядоченная тройка действительных чисел (декартовых прямоугольных координат вектора в ортонормированном базисе).
Рациональное расположение фигуры относительно системы координат (некоторые вершины многогранника находятся на координатных осях), позволяет при решении задач упростить вычисления.
координаты вершин многогранников
вдекартовой системе координат
Вданном пункте представлены в общем виде координаты вершин некоторых видов многогранников, наиболее часто используемых в задачах.
1. Куб ABCDA1B1C1D1 с ребром a.
Пусть начало координат находится в точке A, направление координатных осей показано на рис. 125. Тогда вершины куба имеют координаты:
A(0;0;0), B(0;a;0), C(a; a;0),
D(a;0;0), A1(0;0; a), B1(0; a;a) ,
C1(a;a; a), D1(a; 0; a) .
z y
y
B1  C1
C1
A1 |
D1 |
a |
B |
C |
|
y |
|
|
|
|
|
|
|
|
B |
|
C |
A |
D |
|
|
|
||
A |
D |
x 0 |
|
a x |
Рис. 125
Такое же расположение системы координат удобно использовать для прямоугольного параллелепипеда. Еще один вариант расположения прямоугольного параллелепипеда (куба) относительно декартовой системы координат связан с размещением начала координат в точке пересечения диагоналей основания.
2. Правильная треугольная призма
ABCA1B1C1 , сторона основания которой равна a, а боковое ребро b . Пусть начало координат находится в точке A, ось x направлена вдоль ребра AC , ось y про-
18.02.2011 |
71 |
ходит через точку A перпендикулярно AC , ось z направлена вдоль бокового ребра AA1 (см. рис. 126). Тогда вершины призмы имеют координаты:
|
a |
|
|
a |
3 |
|
|
|
|
|
|||||
A(0;0;0), B |
|
|
; |
|
|
|
|
;0 |
|
, C(a;0;0), |
|||||
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|||||||
A(0;0;b), B |
|
|
|
|
; |
|
|
|
|
|
;b |
, C (a;0;b). |
|||
|
|
|
|
|
|
|
|
||||||||
1 |
1 |
|
2 |
|
2 |
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
z |
B1 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
A1 |
|
|
|
C1 |
|
|
|
3a |
|
B |
|
||||
|
y |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
A |
|
C |
|
|
|
x |
|
|
A |
|
x |
||||
|
|
|
|
|
|
0 |
|
a a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Рис. 126 |
|
|
|
|||||||
Другой вариант расположения правильной треугольной призмы относительно прямоугольной декартовой системы координат показан на рисунке 127.
B1
A1
z

 C1 y
C1 y









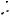

 B
B
A
O
C
 x
x
Рис. 127
3. Правильная шестиугольная приз-
ма ABCDEFA1B1C1D1E1F1 , сторона осно-
вания которой равна a, а боковое ребро b . Пусть начало координат находится в точке A, ось x направлена вдоль ребра AF , ось y проходит через точку A перпендикулярно AF, ось z направлена вдоль бокового ребра AA1 (см. рис. 128). Тогда вершины призмы имеют координаты:
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, C 0;a |
3;0 , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A(0;0;0), B |
|
|
2 |
; |
|
2 |
|
|
;0 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
D(a; a 3;0) , E |
|
|
|
; |
|
|
|
|
|
|
|
|
;0 |
, F(a;0;0), |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A(0; 0;b), |
B |
|
|
|
|
; |
|
|
|
|
|
|
;b |
|
, C (0;a |
|
3;b), |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D (a;a 3;b), E |
|
|
; |
|
|
|
|
|
F(a;0;b). |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
;b , |
||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z C1 |
|
|
|
|
D1 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3a C |
D |
|||||||||||||||||
B1 A1 |
F1 |
|
|
|
E1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
B 3 |
|
|
O |
|
|
|
E |
||||||||
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
||||||||
C |
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
F x |
|||||||||||
B |
|
|
|
|
|
|
|
|
|
a |
|
A |
a a |
|||||||||||||||
A |
F |
|
|
x |
|
|
|
|
0 |
|
|
3a |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
2 |
||||
|
|
|
|
|
|
|
|
|
Рис. 128 |
|
|
|
|
|
|
|
||||||||||||
На выносном чертеже основания AD
BE CF 2a, AC 
 CF2 AF2 a
CF2 AF2 a
 3.
3.
Другой вариант расположения правильной шестиугольной призмы относительно прямоугольной декартовой системы координат представлен на рисунке 129.
z |
E1 |
|
|
D1 |
|
F1 |
|
|
|
||
C1 |
A1 |
y |
|
B1 |
|||
E |
|
||
D |
|
||
|
F |
||
|
|
||
O |
|
|
|
C |
A |
|
|
B |
x |
||
Рис. 129 |
|
||
4. Правильная треугольная пирами- |
|||
да MABC, сторона |
основания которой |
||
равна a, а высота h.
Обычно используют один из двух вариантов расположения системы координат.
4.1.Пусть начало координат находится
вточке A, ось x направлена вдоль ребра AC , ось y проходит через точку A пер-
18.02.2011 |
72 |
пендикулярно AC , ось z проходит через точку A перпендикулярно плоскости ABC (см. рис. 130). Тогда вершины пирамиды имеют координаты:
|
|
|
|
|
|
|
|
a |
|
a |
3 |
|
|
|
|
|
A(0;0;0), B |
|
; |
|
|
;0 |
|
, C(a;0;0), |
|||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||
M |
|
|
; |
|
|
|
|
; h . |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
|
M |
|
|
|
|
|
y |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
|
3a |
|
B |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
B |
|
|
|
|
|
A |
|
C |
|
|||
A |
|
|
|
|
|
|
|
C |
|
x |
|
|
x |
|||
|
|
|
|
|
|
|
|
|
0 |
|
a a |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 130 |
|
|
|
|||
4.2.Пусть начало координат находится
вцентре треугольника ABC в точке O, ось x проходит через точку O параллельно ребру AC , ось y проходит через
точку O перпендикулярно AC , ось z проходит через точку O перпендикулярно плоскости ABC (см. рис. 131). Тогда вершины пирамиды имеют координаты:
|
|
|
a |
|
|
a |
3 |
|
|
|
|
|
|
|
|
|
a |
3 |
|
|
|
||||
|
|
|
; |
;0 |
|
, B |
|
0; |
|
; 0 |
|
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
C |
|
|
; |
|
|
|
|
|
|
;0 |
|
, M(0;0; h). |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
z |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
3a |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
3 |
a |
|
||||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
O |
|
|
|
|
|
|
|
|
|
|
2 |
|
O |
|
2 |
x |
|||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
A |
|
|
|
|
|
|
|
|
C |
|
|
|
|
A |
|
|
|
|
3a C |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Рис. 131 |
|
|
|
|
|
|
|
|
|||||||
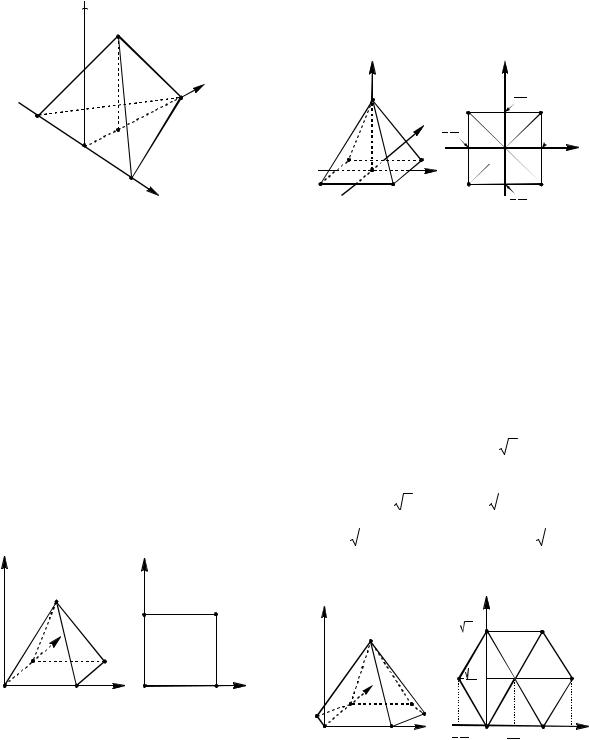
Еще один вариант расположения правильной треугольной пирамиды относительно прямоугольной декартовой системы координат представлен на рисунке
132.
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
z 
M |
|
B |
y |
A |
|
H |
|
O
 C
C
x
Рис. 132
5. Правильная четырехугольная пи-
рамида MABC, сторона основания которой равна a, а высота h.
Обычно используют один из двух вариантов расположения системы координат.
5.1.Пусть начало координат находится
вточке A, ось x направлена вдоль ребра AD, ось y – вдоль ребра AB , ось z
проходит через точку A перпендикулярно плоскости ABC (см. рис. 133). Тогда вершины пирамиды имеют координаты:
|
A(0;0;0), B(0;a;0), |
C(a; a;0), |
||||||
|
D(a;0;0) |
|
a |
|
a |
|
||
|
, M |
|
|
; |
|
|
; h . |
|
|
2 |
2 |
||||||
|
|
|
|
|
|
|||
z |
|
|
|
y |
|
|
|
|
|
M |
|
|
a B |
C |
|||
|
y |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
B |
C |
|
|
|
A |
D |
|
|
|
|
|
|
||||
A |
D |
x |
|
0 |
|
|
a x |
|
|
Рис. 133 |
|
|
|
||||
5.2.Пусть начало координат находится
вцентре основания в точке O, ось x проходит через точку O параллельно ребру AD, ось y проходит через точку
O параллельно ребру AB , ось z проходит через точку O перпендикулярно плоскости основания (см. рис. 134). Тогда вершины пирамиды имеют координаты:
|
|
a |
|
a |
|
|
|
|
a a |
|
|
a |
|
a |
|
|
|||
A |
|
|
; |
|
;0 |
, |
B |
|
|
; |
|
;0 |
, |
C |
|
; |
|
;0 |
, |
|
|
|
|
2 |
|
||||||||||||||
|
2 |
2 |
|
|
|
2 2 |
|
|
|
2 |
|
|
|||||||
18.02.2011
a |
a |
|
, M(0;0; h). |
||||
D |
|
; |
|
;0 |
|
||
2 |
2 |
||||||
|
|
|
|
|
|||
|
z |
|
y |
|
|
M |
B |
a |
C |
|
y |
2 |
||
|
a |
|
a |
|
|
B |
2 |
O |
2 |
|
C |
x |
||
A |
O |
x |
a |
D |
D |
A |
|||
|
|
|
2 |
|
|
Рис. 134 |
|
|
|
6. Правильная шестиугольная пи-
рамида MABCDEF , сторона основания которой равна a, а высота h. Пусть начало координат находится в точке A, ось x направлена вдоль ребра AC , ось y проходит через точку A перпендикулярно AC , ось z проходит через точку A перпендикулярно плоскости ABC (см. рис. 135). Тогда вершины пирамиды имеют координаты:
|
|
a |
|
a 3 |
|
|
|
A(0;0;0), B |
|
|
; |
|
;0 |
|
, |
|
|
||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
C 0;a |
3;0 , D(a; a |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
3;0) , |
|
|
|
|
|
|||||||||||||||||
|
|
3a |
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||
E |
|
|
; |
|
|
|
;0 |
|
, F(a;0;0), M |
|
|
|
; |
|
|
|
|
|
; h . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
M |
|
|
|
|
3a C |
|
|
|
|
D |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
y |
|
|
|
|
B 3 |
a |
|
|
|
|
|
|
O |
|
E |
||||||
|
|
|
|
|
|
|
|
D |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
B |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
F |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
A |
|
|
|
|
|
F |
|
x |
a |
0 |
|
|
|
a |
|
|
a |
|
3a |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 135 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Еще один вариант расположения правильной шестиугольной пирамиды относительно прямоугольной декартовой системы координат показан на рисунке 136.
73
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
|
|
z |
|
|
M |
|
|
y |
|
D |
E |
|
F |
|
|
|
|
C |
|
O |
|
A |
B x
Рис. 136
4.4.Опорные задачи
1.Координаты точки M(x, y, z), де-
лящей отрезок M1M2 между точками
M1(x1, y1, z1) и M2 (x2 , y2 , z2 ) в отноше-
нии M1M :MM2 , определяются формулами
x x1 x2 , y y1 y2 , z z1 z2 .
1 |
1 |
1 |
Доказательство. Рассмотрим векторы
M1M {x x1, y y1, z z1},
MM2 {x2 x, y2 y, z2 z}.
Из равенства M1M MM1 получаем систему для координат векторов
x x1 (x x2 ),
y y1 (y y2 ),
z z1 (z z2 )
или
|
|
x |
x |
2 |
|
|
|
|||
x |
1 |
|
|
|
, |
|||||
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
y |
y |
|
|
|
|
||||
|
|
2 |
|
|||||||
y |
|
1 |
|
|
|
, |
||||
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
z |
z |
2 |
|
|
|
|||
z |
|
1 |
|
. |
||||||
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
||
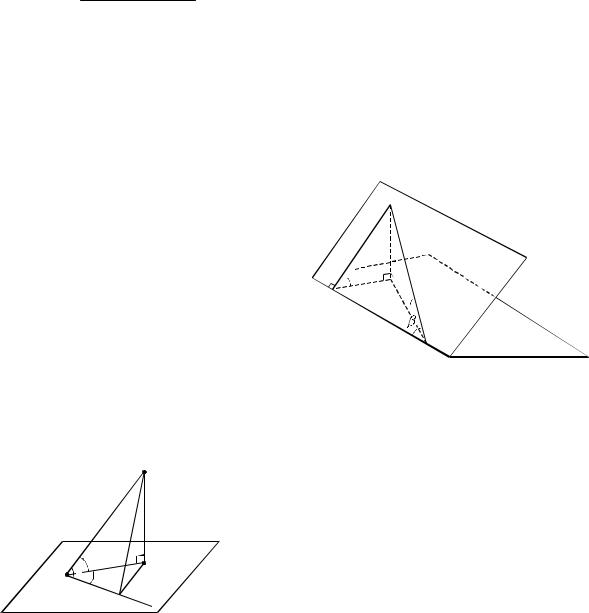
2. Трехгранным углом называется фи-
гура, состоящая из нескольких лучей OA, OB, OC , выходящих из одной точки O и не лежащих в одной плоскости, и из плоских углов AOB, BOC, AOC между этими лучами (см. рис. 137). Точка O называется вершиной трехгранного угла,
18.02.2011 |
74 |
лучи OA, OB, OC – ребрами, части плоскостей, заключенные между ребрами, называются гранями, а углы AOB, BOC, AOC , образованные ребрами, лежащими в одной грани, называются плоскими углами трехгранного угла.
|
|
|
|
C |
|
|
|
C1 |
|
|
|
x |
C A1 |
|
|
|
|
|
|
O |
|
|
A |
|
|
|
|||
|
|
|
B1 |
B |
|
|
|
|
Рис. 137
Теорема. Во всяком трехгранном угле, плоские углы которого равны , и , а двугранные углы, противолежащие им, соответственно равны A , B и C ,
имеют место следующие равенства:
cos C cos cos cos , sin sin
cos B cos cos cos , sin sin
cos A cos cos cos .
Доказательство. Докажем, например, первое равенство. Пусть в трехгранном
угле |
OABC плоские углы при вершине |
||
O |
равны |
BOC , |
AOC , |
AOB |
(см. рис. 137). |
Через произ- |
|
вольную точку C1 ребра |
OC проведем |
||
плоскость перпендикулярную этому ребру. Пусть B1 и A1 точки пересечения этой плоскостью ребер OB и OA, соответственно. По условию линейный угол B1C1A1 двугранного угла с ребром OC
равен C . Пусть OC1 x. В треугольни-
ке OB C C B x tg , |
OB |
x |
. В |
||||
|
|||||||
|
1 1 1 |
1 |
1 |
|
cos |
||
треугольнике |
OA1C1 |
C1A1 x tg , |
|||||
OA |
x |
. |
Из теоремы косинусов для |
||||
|
|||||||
1 |
cos |
|
|
|
|
|
|
треугольников OB1C1 и B1C1A1 |
получаем: |
||||||
B1A12 OB12 OA12 2 OB1 OA1 cos ;
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
B1A12 C1B12 C1 A12 2 C1B1 C1 A1 cos C .
Приравняем правые части равенств и подставим выражения OB1, OA1, C1B1,
C1A1: |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
x |
|
2 |
x |
|
x |
|
|
|
|
|
|
|
2 |
|
|
|
cos |
|
|
|
|
|||||||
cos |
|
|
|
|
cos |
|
cos |
|
||
cos |
|
|
|
|||||||
(xtg )2 (xtg )2 2 x2 tg tg cos C .
После преобразований получаем доказываемую формулу:
cos C cos cos cos .
Аналогично доказываются два других равенства. Данную теорему называют «тео-
ремой косинусов для трехгранного угла».
3. Теорема («о трех косинусах»).
Пусть величина угла между наклонной l и ее проекцией на некоторую плоскость, величина угла между проекцией наклонной l и прямой, проведенной через основание той же наклонной в плоскости проекции, и величина угла между наклонной l и прямой, проведенной через ее основание в плоскости проекции. Тогда справедливо следующее соотношение:
cos cos cos .
Доказательство. Выберем точку A
на прямой l, пересекающей плоскость в точке B (см. рис. 138), и спроектируем ее на плоскость ( AO ). Пусть точка D основание перпендикуляра, опущенного из точки O на прямую BC. Тогда в
|
|
A |
|
l |
|
|
|
O |
|
|
|
|
|
D

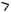 C
C
Рис. 138
соответствии с условием ABO ,
OBC , |
ABC . Треугольники |
AOB, BOD, |
ABD – прямоугольные. То- |
18.02.2011 |
75 |
гда из треугольника AOB BO ABcos ,
из |
треугольника |
BOD |
|
BD BOcos ABcos cos , |
из |
тре- |
|
угольника |
ABD BD ABcos . Из |
по- |
|
следних двух равенств следует:
cos cos cos .
Замечание. Теорема «о трех косинусах» является следствием «теоремы косинусов для трехгранного угла» в случае, если C 90 .
4.Теорема («о трех синусах»). Пусть
водной из граней двугранного угла, величина которого равна , проведена прямая, составляющая с ребром двугранного угла угол (0 /2), – величина
угла между этой прямой и другой гранью (см. рис. 139). Тогда справедливо следующее соотношение:
sin sin sin .
Доказательство. Пусть AD
A





B |
C |
|
|
|
D |
|
Рис. 139 |
данная в условии прямая; точка C основание перпендикуляра, опущенного из точки A на плоскость , и ABC линейный угол двугранного угла BD (см. рис. 139). Тогда в соответствии с условием
ABC , ADB и ADC .
Пусть AD x. Тогда для прямоугольных треугольников справедливо: для тре-
угольника |
ADB |
AB xsin , для тре- |
угольника |
ABC |
AC xsin sin и для |
треугольника ADC
sin AC: AD sin sin .
Следовательно, sin sin sin .
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
5. Если некоторая прямая образует с тремя попарно перпендикулярными прямыми углы , и , то выполняется равенство
cos2 cos2 cos2 1.
Доказательство. Достаточно рас-
смотреть прямоугольный параллелепипед ABCDA1B1C1D1 с диагональю DB1 1.
Пусть CDB1 , ADB1 ,
B1DD1 (см. рис. 140). Тогда в соответствующих прямоугольных треугольниках CD cos , AD cos , DD1 cos . Так как DB12 CD2 AD2 DD12 , то имеем
cos2 cos2 cos2 1.
B1 |
|
|
C1 |
A1 |
D1 |
|
|
B |
C |
|
A
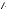





D
Рис. 140
В качестве следствия получим
sin2 sin2 sin2 2.
6. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.
Sпр S cos ,
где S – площадь многоугольника, лежащего в плоскости , Sпр – площадь его ортогональной проекции на плоскость .
Доказательство. Так как много-
угольник можно разбить на конечное число треугольников, и фигуру можно параллельно перенести в равную ей фигуру, то достаточно рассмотреть треугольник, через одну сторон которого проходит плоскость (например, через сторону AB ) (см. рис. 141).
18.02.2011 |
76 |
C
A
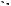
Рис. 141
Если D – проекция точки C на плоскость , то ABD – проекция треугольника АВС на эту плоскость. Пусть СМ – высота в треугольнике АВС, тогда по теореме о трех перпендикулярах DM AB.
Обозначим CMD . Имеем последовательно площади треугольников
S |
ABC |
|
1 |
AB CM , |
S |
ABD |
|
1 |
AB DM , |
|
2 |
|
|
2 |
|
||||
DM CM cos , |
SABD SABC cos . |
||||||||
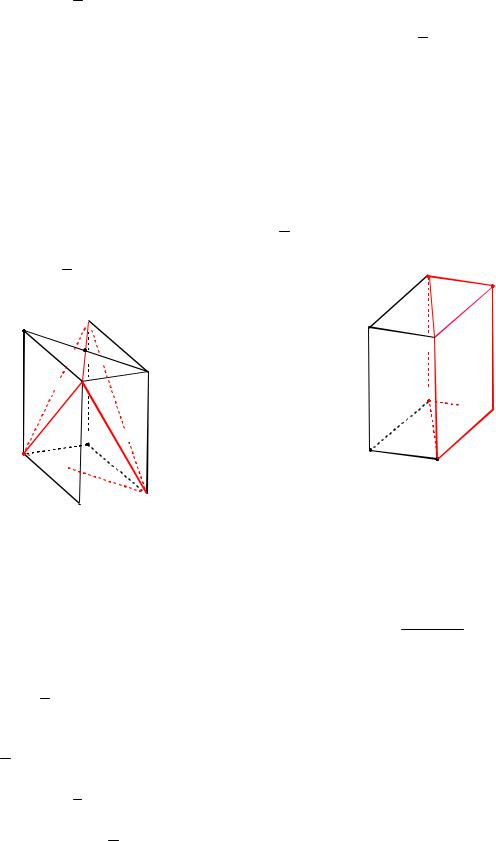
7. Если вершины А, В, D и A1 паралле-
лепипеда ABCDA1B1C1D1 являются вершинами тетраэдра, то имеет место равенство
1
VABDA1 6VABCDA1B1C1D1 .
|
D1 |
|
C1 |
A1 |
|
B1 |
||
|
||
|
D |
|
C |
M A |
B
Рис. 142
Доказательство. Тетраэдр и параллелепипед имеют одну высоту A1M h (см. рис. 142). Для площадей оснований име-
ем соотношение S |
ABD |
|
1 |
S |
ABCD |
. Тогда |
|||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
VABDA |
|
1 |
h |
1 |
SABCD |
|
1 |
VABCDA B C D . |
|||||||||
|
2 |
|
|||||||||||||||
1 |
3 |
|
|
|
6 |
|
|
1 |
1 |
1 |
1 |
||||||
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
8. Если вершины А, В, С и D параллелепипеда AKBMQCLD являются вершинами тетраэдра, то имеет место равенство
1
VABCD 3VAKBMQCLD .
Доказательство. Так как объемы угловых тетраэдров равны и составляют шестую часть от объема параллелепипеда V, то имеем
VABCD |
V 4 |
1 |
V |
1 |
V . |
|
|
||||
|
6 |
3 |
|
||
9. Пусть a и b – длины двух противоположных ребер тетраэдра, d – расстояние, – угол между ними. Тогда объем тетраэдра может быть вычислен по формуле
V1 abdsin . 6
D
Q

 E
E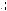





 L
L
 C
C 

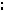
 M
M 
A 





 B
B
K
Рис. 143
Доказательство. Достроим данный тетраэдр ABCD до параллелепипеда AKBMQCLD (см. рис. 143), проводя через каждое ребро плоскость, параллельную противоположному ребру. Пусть AB a, CD b, тогда площади граней AKBM и
LCQD равны 1 absin , расстояние меж- 2
ду ними d. Тогда объем параллелепипеда
равен 1 abd sin . Объем пирамиды
2
ABCD составляет 1 от объема паралле- 3
лепипеда, то есть равен 1abd sin . 6
18.02.2011 |
77 |
10. Пусть q – площадь одной из боковых граней треугольной призмы, d – расстояние от противоположного ребра до этой грани. Тогда объем этой призмы может быть найден по формуле
V1 qd . 2
Доказательство. Пусть площадь грани AA1D1D равна q, а расстояние от СС1 до этой грани равно d (см. рис. 144). Объем параллелепипеда ABCDA1B1C1D1 равен qd . Так как объем этого параллелепипеда в два раза больше объема призмы ACDA1С1D1 , то объем этой призмы равен
1 qd .
2
C1 D1
D1
B1


 A1
A1
C





 D
D
B
A
Рис. 144
11. Пусть p и q – площади двух граней тетраэдра, a – длина общего ребра,– величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле
V 2pqsin .
3a
Доказательство. Пусть площади граней АВС и ACD тетраэдра ABCD равны p и q соответственно, – угол между
этими гранями, AC a (см. рис. |
145). |
||||
Высота DH треугольника ACD |
равна |
||||
|
2q |
. Для высоты пирамиды имеем |
|
||
|
|
|
|||
|
a |
|
|||
|
|
DO DH sin |
2qsin |
. |
|
|
|
|
|
||
|
|
|
a |
|
|
Тогда объем пирамиды ABCD равен
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
V |
1 |
p DO |
2pqsin |
. |
|
|
|||
3 |
|
3a |
||
|
|
|
D |
|
B 







 A
A
O



 H
H
 C
C
Рис. 145
12. Пусть в пирамиде MABC на ребрах MA, MB и MC или на их продолжениях
взяты соответственно точки A1, B1, C1
так, что MA1 :MA k , |
MB1 :MB m, |
MC1 :MC n. Тогда объемы пирамид MA1B1C1 и MABC связаны формулой
VMA1B1C1 k m n VMABC .
|
|
|
|
M |
|
|
|
|
|
H |
|
|
|
|
|
C1 |
|
|
|
A1 |
|
||
|
|
F |
B1 |
|
|
|
A |
|
|
||
|
|
E |
|
C |
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
Рис. 146 |
|
|
Доказательство. Из точек С1 и С |
||||
проведем к плоскости ABМ перпендику- |
|||||
ляры С1H и CF соответственно (см. рис. |
|||||
146). Тогда |
С1H ||CF и из подобия тре- |
||||
угольников |
С1HM и СFM |
получаем |
|||
C H |
MC1 |
CF n CF . Из |
сравнения |
||
|
|||||
1 |
|
MC |
|
|
|
|
|
|
|
||
площадей треугольников с общим углом имеем SMA1B1 k m SMAB . Для тетраэдров
MA1B1C1 и MABC с основаниями MA1B1 и MAB получаем
1
VMA1B1C1 3C1H SMA1B1
1n CF k m SMAB k m n VMABC . 3
13.Объем треугольного призматического тела ABCA1B1C1 , ограниченного
треугольниками ABC и A1B1C1, можно вычислить по формуле
VABCA B C |
|
AA1 BB1 CC1 |
SABC , |
||
|
|||||
1 |
1 |
1 |
3 |
|
|
|
|
|
|||
где плоскость АВС перпендикулярна ребрам призматической поверхности,
AA1 BB1 CC1.
Доказательство. 1. Разделим призма-
тическое тело ABCA1B1C1 на три части плоскостями A1B0C1 и A1B0C0 (парал-
лельно ABC): треугольную призму ABCA1B0C0 , две треугольные пирамиды
A1B0C0C1 и A1B0B1C1 (см. рис. 147).
2. Пусть SABC S , AA1 a, BB1 b,
CC1 c . Тогда объем прямой призмы
ABCA1B0C0 равен aS .
 C1
C1
B1




 C2
C2
B0











 C0
C0
 A1
A1
B












 C
C
 A
A
 A3
A3
B3
 C3
C3
Рис. 147
3. Для пирамиды A1B0C0C1 , принимая треугольник A1B0C0 за основание, объем
равен 1(c a)S . 3
4. Пусть C0C2 B0B1. Тогда для пирамид A1B0B1C1 и A1B0C2C0 с общей вер-
18.02.2011 |
78 |
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
шиной A1 |
|
|
и равновеликими основаниями |
|
VSABC |
|
|
|
|
|
|
|
|
|
1 |
|
SO SABC |
|
|
|
|
|
|
|
SSAC |
|
SABC |
|||||||||||||||||||||||||||||||||||||||||||||
B BC и B C |
C |
|
|
объемы равны. |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
0 |
1 |
|
1 |
|
|
|
|
0 |
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1B0B1C1 |
|
VS1A1B1C1D1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SA1S1D1 |
SA1B1C1D1 . |
||||||||||||||||||||||||
|
Значит, |
объем пирамиды |
ра- |
|
|
|
|
S O S |
A B C D |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
вен |
(b a)S . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
|
||||||
|
5. Окончательно объем призматиче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
ского тела ABCA1B1C1 |
равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
aS |
1 |
(c a)S |
1 |
(b a)S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a b c |
S |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O1 |
|
M1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
14. Объем треугольного призматиче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
ского тела A1B1C1A3B3C3 , |
|
|
ограниченного |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|||||||||||||||||||||||||||||||||||||
треугольниками A1B1C1 |
и A3B3C3 , можно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 148 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
вычислить по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
VA B C A B C |
|
A1A3 |
B1B3 |
C1C3 |
|
SABC , |
|
|
|
|
|
|
VSABC |
|
|
|
|
|
|
SSAC SABC |
|
|
, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
1 |
1 |
1 |
3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VS A B C D |
|
SA S D SA B C D |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
||||||||
где плоскость АВС перпендикулярна реб- |
|
что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рам призматической поверхности (дока- |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Замечание. |
|
|
Приведенное |
доказатель- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
жите самостоятельно). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ство не зависит от того, какие много- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
15. Если в двухпирамидах, имеющихпо |
|
угольники лежат в основании пирамид. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равному двугранному углу при основании, |
|
Если же ребра равных двугранных углов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равны также и ребра этих углов, то отно- |
|
в рассматриваемых пирамидах не равны |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
шение объемов этих пирамид равно отно- |
|
между собой, то отношение объемов этих |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
шению произведений площадей граней, |
|
пирамид прямо пропорционально произ- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
образующихравные двугранные углы. |
|
|
ведениям площадей граней, образующих |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Доказательство. |
Пусть |
|
пирамиды |
|
эти углы, |
|
|
|
и |
|
|
обратно |
пропорционально |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
длинам их ребер, т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
SABC и SA1B1C1D1 (см. рис. 148), имеют |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
VSABC |
|
|
|
|
|
|
|
|
SASB SABC |
|
|
|
A1D1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
равные |
|
|
двугранные |
|
|
|
углы |
|
SACB |
и |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
VS AC D |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S A D C , |
также |
|
|
AC A D . Построим ли- |
|
|
|
|
|
SAS D |
SABC D |
|
|
AC |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
|
|
|
|
1 |
1 |
1 |
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
||||||||||||||
нейные углы SMO и S1M1O1 |
данных рав- |
|
Кроме того, |
|
справедливы следующие |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ных |
|
двугранных |
углов. |
|
|
По |
|
|
условию |
|
теоремы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
SMO S1M1O1 . Тогда прямоугольные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
16. Если в пирамиде провести секу- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
треугольники MSO и M1S1O1 |
подобны и |
|
щую плоскость параллельно основанию, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
SM |
|
|
SO |
. |
|
|
|
|
|
|
то она отсечет от нее другую пирамиду, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подобную данной (докажите самостоя- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S1M1 S1O1 |
|
|
|
|
|
|
тельно). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Площади боковых граней SAC и S1A1D1 |
|
17. Поверхности подобных много- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
относятся |
|
|
|
как |
|
|
их высоты, поскольку |
|
гранников относятся как квадраты сход- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ственных |
|
|
|
линейных |
|
элементов |
|
много- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AC A1D1 , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гранников (докажите самостоятельно). |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
SSAC |
|
|
|
|
SM |
|
|
|
|
|
|
|
|
SO |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
18. Объемы подобных многогранников |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
SA S D |
|
|
S1M |
1 |
|
|
|
|
S1O1 |
|
|
|
|
относятся как кубы сходственных линей- |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных элементов этих многогранников (до- |
||||||||||||||||||||||||||||||||||||||
|
Найдем |
|
отношение |
объемов |
данных |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
кажите самостоятельно). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
пирамид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18.02.2011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
79 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
19.Квадраты объемов подобных многогранников относятся как кубы площадей сходственных граней (докажите самостоятельно).
20.Плоскости BDC1 и B1D1A перпен-
дикулярны диагонали A1C куба
ABCDA1B1C1D1 и делят ее на три равные части.
Доказательство. 1. Так как AB1 ||DC1
и AD1 ||BC1 , то плоскости BDC1 и B1D1A
(см. рис. 149).
2. Достаточно доказать перпендикулярность прямой A1C, содержащей диа-
гональ куба, к одной плоскости BDC1 . Так как диагонали BD и АС в квадрате
ABCD взаимно перпендикулярны и АС является проекцией A1C на плоскость ABC, то по теореме о трех перпендикулярах A1C BD. Аналогично A1C DC1 .
Следовательно, A1C BDC1.
|
B1 |
A1 |
C1 |
|
|
|
D1 |
|
E |


 B
B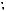
 F
F


A C
C
D
Рис. 149
3. Для куба с ребром а диагональ
A1C a
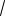 3, а расстояние от точки C до
3, а расстояние от точки C до
плоскости BDC1 равно a 3 (см. пример
3
16). Аналогично расстояние от точки A1
до плоскости B D A равно |
a 3 |
. Значит, |
|
|
|||
1 |
1 |
3 |
|
|
|
|
|
диагональ куба делится указанными плоскостями на три равные части.
21. Сечение, проходящее через диагональ параллелепипеда, делит его противоположные ребра, пересекаемые плоскостью сечения, в обратном отношении, считая от любой грани, из которой выходят эти ребра, а сам параллелепипед – на два равновеликих многогранника.
18.02.2011 |
80 |
C1
D1
B1

 M1
M1
N


 C
C 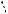 A1
A1 

 M
M
N1




D
B
A
Рис. 150
Доказательство. Рассмотрим общий случай наклонного параллелепипеда ABCDA1B1C1D1 (см. рис. 150). Пусть се-
чение проходит через диагональ AC1 и
пересекает ребра BB1 и CC1 в точках N и М соответственно. Сечение, содержащее AC1 , всегда будет являться параллелограммом, поскольку в сечении получается четырехугольник, противоположные пары сторон которого параллельны (по свойству параллельных плоскостей, пересекаемых плоскостью). При этом точка пересечения диагоналей параллелограмма совпадает с центром параллелепипеда.
Если точка N совпадает с одной из точек B или B1 (следовательно точка М с
одной из точек D1 или D соответственно), то получается диагональное сечение, разбивающее параллелепипед на две равные призмы.
Пусть, точка N не совпадает ни с одной из точек B или B1. Так как
C1M || AN , то из равенства треугольников
C1D1M и ABN следует, что D1M BN .
Отсюда MD NB1 . Тогда DM B1N .
MD1 NB
Заметим, что секущая плоскость разбивает параллелепипед на два много-
гранника C1MDCNAB и ANB1A1MC1D1 ,
которые симметричны относительно центра параллелепипеда. Из следующего соответствия вершин первого и второго
многогранников |
D B1, |
M N, |
A C1, C A1, |
B D1, |
N M, |
C1 A следует, что они равны. Следовательно, они имеют равные объемы.
В случае пересечения секущей плоскостью ребер A1D1 или B1A1 доказательство проводится аналогично.
www.alexlarin.narod.ru
