
C2-2011
.pdf
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
(D1, AB1C) 
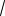 3 2 2
3 2 2
 3 . 3 3
3 . 3 3
Ответ: 2 3 . 3
Пример 18. Точки A, B, C, D являются вершинами параллелограмма, ни одна из сторон которого не пересекает плоскость . Точки A, B, C удалены от плоскости на расстояние 2, 3, 6 соответственно. Найти расстояние от вершины D до плоскости .
|
B |
C |
|
O |
|
A |
|
D |
B1 |
O1 |
C1 |
A1 |
|
D1 |
Рис. 16
Решение. Опустим перпендикуляры из вершин A, B, C и D на плоскость .
Точки A1, B1,C1, D1 – их ортогональные проекции на (см. рис. 16).
Точка O – точка пересечения диагоналей параллелограмма ABCD, которая проектируется в точку O1 – точку пересечения диагоналей параллелограмма A1B1C1D1 (по свойству проекций). Так как точка O делит отрезки AC и BD пополам, то по свойству проекций отрезков
точка |
O1 также |
делит отрезки A1C1 и |
||||||
B1D1 пополам. Четырехугольники C1CAA1 |
||||||||
и D1DBB1 – трапеции. Отрезок OO1 |
их |
|||||||
средняя линия. Тогда |
|
|
|
|||||
|
|
CC1 AA1 |
|
DD1 |
BB1 |
. |
|
|
|
|
|
|
2 |
|
|||
|
2 |
|
|
|
|
|
||
Отсюда DD1 CC1 AA1 BB1 и, |
так |
|||||||
как |
CC1 6, |
BB1 3, |
AA1 2, |
то |
||||
DD1 5. |
|
|
|
Ответ: 5. |
||||
|
|
|
|
|
|
|||
18.02.2011 |
11 |
1.4. Расстояние между скрещивающимися прямыми
Расстояние между двумя скрещиваю-
щимися прямыми равно длине отрезка их общего перпендикуляра.
поэтапно-вычислительный метод
Для нахождения расстояния между скрещивающимися прямыми можно воспользоваться одним из приведенных ниже четырех способов.
1.Построить общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный обеим) и найти его длину.
2.Построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстояние от какой-нибудь точки второй прямой до построенной плоскости.
3.Заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, и найти расстояние между этими плоскостями.
4.Построить плоскость, перпендикулярную одной из данных прямых, и построить на этой плоскости ортогональную проекцию второй прямой (см. рис. 17).
|
C |
l1 |
l2 |
|
|
|
C1 |
A |
H |
|
Рис. 17
(l1, l2 ) (A, BC1) AH,
где A l1 , l1, BC1 ортогональ-
ная проекция l2 на плоскость , H основание перпендикуляра, опущенного из A на BC1.
Пример 19. В кубе, длина ребра которого равна a, найти расстояние между ребром и диагональю, не пересекающей его грани.
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Решение. В качестве примера найдем расстояние между ребром AA1 и диаго-
налью D1C (см. рис. 18). Прямые AA1 и D1C скрещивающиеся. Используя каждый из отмеченных способов, покажем, что расстояние между ними равно a .
1-й способ (см. рис. |
18а). Так как |
|||||
A1D1 AA1 и |
A1D1 D1C , то A1D1 общий |
|||||
перпендикуляр двух |
скрещивающихся |
|||||
прямых AA1 |
и D1C. Расстояние между |
|||||
|
B1 |
C1 |
|
B1 |
C1 |
|
A1 |
D1 |
A1 |
D1 |
d |
||
a |
B |
d |
a |
B |
||
C A |
C |
|||||
A |
|
A |
D |
|||
|
D |
|
||||
аб
|
B1 |
C1 |
|
B1 |
C1 |
|
A1 |
D1 |
d |
A1 |
|
D1 |
|
a |
B |
a |
B |
d |
||
C A |
C |
|||||
A |
D |
A |
|
|||
|
D |
вг
Рис. 18
AA1 и DD1C1 равно A1D1 a .
2-й способ (см. рис. 18б). Так как плоскость DD1C1, содержащая D1C, па-
раллельна AA1, то расстояние от AA1 до DD1C1 равно a .
3-й способ (см. рис. 18в). Плоскость DD1C1, содержащая D1C, параллельна плоскости AA1B1 , содержащей AA1, и расстояние между ними равно a.
4-й способ (см. рис. 18г). Плоскость ABC перпендикулярна прямой AA1. Точ-
ка A проекция AA1 на эту плоскость. Проекцией D1C на плоскость ABC является DC. Расстояние от точки A до DC. равно a.
Ответ: a.
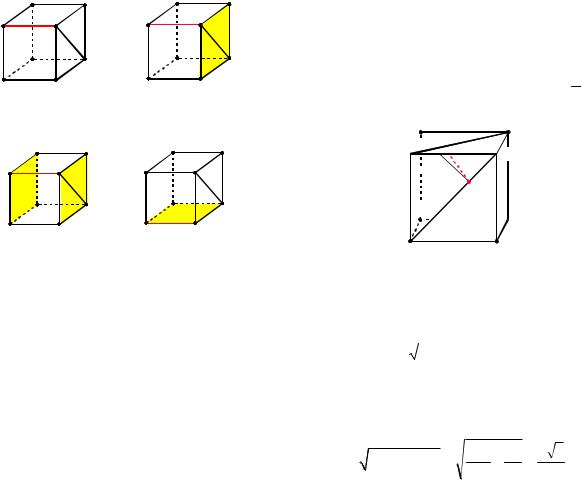
Пример 20. Найти расстояние между непересекающимися диагоналями двух смежных граней куба, длина ребра которого равна a.
Решение. Найдем расстояние между диагоналями A1C1 и AD1 куба
ABCDA1B1C1D1 .
1-й способ. Пусть отрезок PQ (см. рис. 19) есть общий перпендикуляр скрещи-
вающихся прямых A1C1 |
и AD1 , а PN и |
||||
KQ его |
ортогональные |
проекции на |
|||
плоскости A1B1C1 и AA1D1 соответственно |
|||||
(PK A1D1 |
и |
QN A1D1). |
На основании |
||
теоремы |
|
о |
трех |
перпендикулярах |
|
PN AC |
и |
KQ AD . |
Треугольники |
||
1 |
1 |
|
1 |
|
|
A1PN и |
KQD1 прямоугольные и равно- |
||||
бедренные, поэтому A1K KN ND1 a . 3
B1 C1
A1
 P
P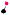
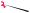

 N
N  D1
D1
 K
K
Q
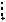 B
B












 C
C
A D
Рис. 19
Аналогично, |
NQ ND |
A K KP |
a |
|
||||
|
||||||||
|
|
1 |
1 |
3 |
|
|||
|
|
|
|
|
|
|
|
|
и AP PN |
a |
|
2 |
|
. Тогда из прямоуголь- |
|||
1
3
ного треугольника PNQ получим расстояние между A1C1 и AD1 :
PQ PN2 NQ2 
 2a2 a2 a
2a2 a2 a
 3 .
3 .
9 9 3
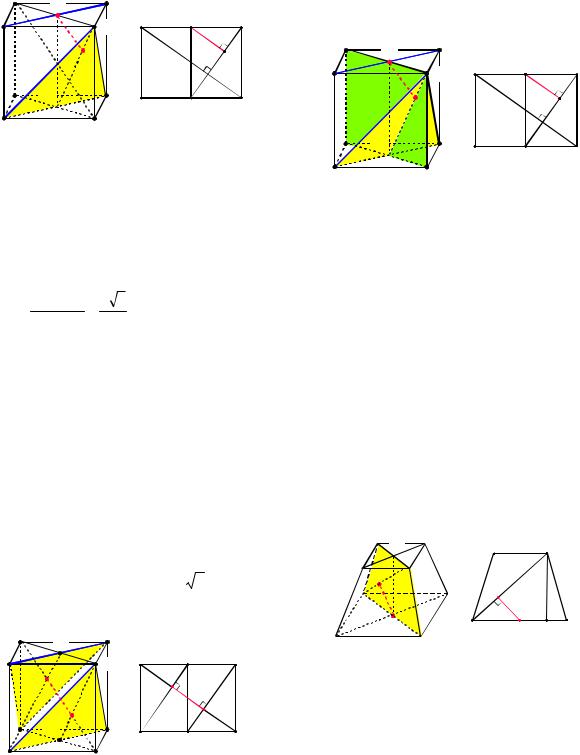
2-й способ. Построим плоскость, содержащую AD1 и параллельную A1C1 (см. рис. 20а). Искомой плоскостью является AD1C . Найдем расстояние до нее от ка- кой-либо точки прямой A1C1. Для этого опустим из точки O (см. рис. 20а) на указанную плоскость перпендикуляр. Плоскости BB1D1 и AD1C перпендикулярны
( AC BD и AC D1D , и AC AD1C ).
18.02.2011 |
12 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
B1 O |
C1 |
B1 |
O |
D1 |
A1 |
D1 |
|||
N |
|
|
h |
N |
B O1 |
C |
B |
O1 |
D |
|
|
AD
аб
Рис. 20
Так как B1D D1O1 (см. рис. 20б) (докажите самостоятельно!), то ON AD1C
(ON || B1D) и из подобия треугольников
BB D |
и OD N следует |
ON |
|
OD1 |
или |
|
|
||||
1 |
1 |
BD |
|
B1D |
|
|
|
|
|||
h ON BD OD1 a
 3 . B1D 3
3 . B1D 3
Замечание. Для нахождения расстояния от точки О до плоскости AD1C можно воспользоваться результатом примера 10.
3-й способ. Построим параллельные плоскости AD1C и BA1C1 (см. рис. 21а), содержащие прямые AD1 и A1C1 соответственно. Диагональ B1D куба перпендикулярна обеим плоскостям и (см. рис. 21б) точками K и N делится на три равные части (опорная задача 20). Расстояние между плоскостями AD1C и BA1C1
равно длине отрезка KN , т.е. |
a 3 |
. |
|
|||
3 |
|
|||||
|
|
|
|
|
|
|
B1 |
O |
C1 |
B1 |
O |
D1 |
|
A1 |
K |
D1 |
||||
|
|
K |
h |
|
||
|
|
N |
|
|||
B |
|
|
|
N |
|
|
O1 |
C |
B |
O1 |
D |
||
|
|
|
||||
AD
аб
Рис. 21
4-й способ. Плоскость BB1D1 перпен-
дикулярна |
прямой |
A1C1 ( A1C1 B1D1 и |
|
A1C1 D1D ) |
и |
плоскости |
AD1C |
(B1D AD1C ) (см. рис. 22а). D1O1 про- |
|||
екция AD1 |
на плоскость BB1D1 . Расстоя- |
||
ние от точки O (проекции A1C1 |
на плос- |
||
18.02.2011 |
|
|
13 |
кость BB1D1 ) до D1O1 равно длине отрезка
ON (см. рис. 22б).
B1 O |
C1 |
B1 |
O |
D1 |
A1 |
D1 |
|||
N |
|
|
h |
N |
B O1 |
C |
B |
O1 |
D |
|
|
AD
аб
Рис. 22
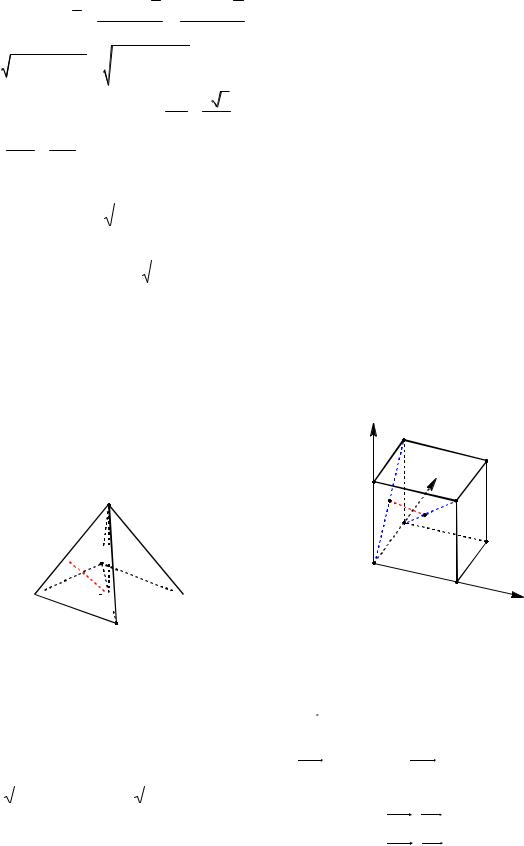
Пример 21. В правильной усеченной четырехугольной пирамиде ABCDA1B1C1D1 со сторонами оснований равными a и b (a b), и высотой h найти расстояние между диагональю BD1 и диагональю большего основания AC .
Решение. Прямые BD1 и AC скрещиваются (см. рис. 23а). Точки O и O1 точки пересечения диагоналей оснований пирамиды. OO1 AC и OO1 BD , как отрезок, соединяющий середины оснований равнобедренных трапеций BB1D1D и AA1C1C.
B1 O1 |
C1 |
B1 |
D1 |
A1 |
D1 |
|
|
K |
C |
K |
|
B |
|
||
|
|
|
|
O |
|
B |
O N D |
AD
аб
Рис. 23
Построим плоскость перпендикулярную одной из скрещивающихся прямых BD1 и AC . Плоскость BB1D1 AC , так как AC перпендикулярна двум пересекающимся прямым этой плоскости:
AC BD ( ABCD квадрат) и AC OO1
(OO1 высота пирамиды). Прямая BD1 лежит в плоскости BB1D1 , поэтому искомое расстояние равно длине перпендикуляра, опущенного из точки O на BD1. OK найдем из подобия прямоугольных
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
треугольников BD1N и BKO (см. рис. 23б), имеющих общий острый угол. В
треугольнике BD1N : D1N h, |
BN |
BD ND a
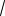 2 (a b)
2 (a b)
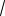 2 (a b)
2 (a b)
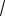 2 ,
2 ,
|
|
|
|
2 |
|
|
|
2 |
BD |
|
|
h2 |
(a b)2 |
. |
|
||
D N2 |
BN2 |
|
||||||
|
|
|||||||
1 |
1 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|||
В треугольнике BKO BO BD a 2 .
2 .
2 2
Тогда OK BO или
D1N BD1
OK |
BO D1N |
|
|
|
ah |
|
. |
|
|
|
BD1 |
|
|
|
|
|
|
|
|
||
|
|
2h2 (a b)2 |
||||||||
|
|
|
|
|
|
|
||||
|
Ответ: |
|
ah |
|
|
|
. |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2h2 (a b)2 |
||||
Пример 22. В правильной четырех- |
||||||||||
угольной пирамиде |
|
SABCD, все |
|
ребра |
||||||
которой равны 1, найти расстояние между прямыми BD и SA.
Решение. Пусть E – основание перпендикуляра (см. рис. 24), опущенного из точки O на ребро SA. Так как прямая BD перпендикулярна плоскости AOS, то
BD OE .
S
E
 B
B

A









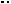 O
O





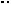
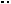




 C
C
D
Рис. 24
Таким образом, ОЕ – общий перпендикуляр к скрещивающимся прямым BD и SA. Найдем его длину, вычислив двумя способами площадь треугольника AOS.
Из |
равенства |
AO SO AS OE, где |
|||||||
AO |
|
2 |
|
, AS 1, |
SO |
|
2 |
|
следует, что |
|
2 |
|
|
2 |
|
|
|||
OE 0,5.
Ответ: 0,5.
векторно-координатный метод
Пример 23. В единичном кубе ABCDA1B1C1D1 найти расстояние меж-
ду диагональю куба BD1 и диагональю грани AB1 .
Решение. Введем прямоугольную систему координат (см. рис. 25), тогда
А(0;0;0), В(0;1;0), В1(0;1;1), |
D1(1;0;1). |
||||||
Пусть EF – общий перпендикуляр |
|||||||
скрещивающихся прямых BD1 |
и AB1 , то |
||||||
есть EF AB1, |
EF BD1 , |
причем |
|||||
E AB |
и F BD . Обозначим |
AE |
, |
||||
|
|||||||
1 |
|
1 |
|
B1E |
|||
|
BF |
|
|
|
|||
|
и воспользуемся формулами для |
||||||
D1F |
|||||||
|
|
|
|
|
|
||
координат точки (опорная задача 1), которая делит данный отрезок в заданном
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отношении. |
Получим E |
0, |
|
|
|
, |
|
, |
|||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
F |
|
|
, |
|
|
|
|
, |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 1 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
z |
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A1 |
|
|
|
|
y |
|
|
|
|
C1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
E |
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
||
|
|
|
|
|
A |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 25 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть |
|
|
|
|
|
p, |
|
|
|
|
q, |
тогда |
|||||||||||
|
1 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
E(0, p, p), F(q,1 q, q). |
Так как вектор |
||||||||||||||||||||||
EF {q, |
|
1 q p, q p} |
|
должен |
быть |
||||||||||||||||||
перпендикулярным |
|
|
|
|
|
|
|
векторам |
|||||||||||||||
AB1 |
{0;1;1} |
|
и BD1 {1; 1;1}, |
то имеем |
|||||||||||||||||||
систему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
AB EF 0, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
или |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
EF 0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
BD1 |
|
|
|
|
|
|
|
|
|
||||||||
18.02.2011 |
14 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
1 q p q p 0, |
|
p |
1 |
|
, q |
|
1 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||
q 1 q p q p 0 |
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
Отсюда EF |
|
1 |
|
1 |
|
|
|
1 |
|
|
EF |
|
EF |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9 |
36 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
векторный метод
Пример 24. В единичном кубе ABCDA1B1C1D1 найти расстояние меж-
ду прямыми AB1 и BD.
Решение. |
Пусть |
AD a , |
AB b , |
AA1 c (см. |
рис. 26), |
тогда |
|a | |b | |
|c | 1, a b a c b c 0.
B1
A1
 C1
C1
M
 B
B
 D1
D1
A


 N
N


 C
C
D
Рис. 26
Если M и N – основания общего перпендикуляра прямых AB1 и BD соответ-
ственно, |
то |
имеем |
AB1 b c, |
DB b a,
MN MA AD DN
x AB1 a y DB
x(b c) a y(b a)
(1 y) a (x y) b x c .
Вектор MN перпендикулярен векто-
рам AB1 и DB, поэтому имеем
MN AB1 0,


MN DB 0
|
|
(x y) b |
|
(b |
|
|
(1 y) a |
x c |
c) 0, |
|
|||
|
|
|
|
|
|
|
|
(x y) b |
(b |
|
|||
(1 y) a |
x c |
a) 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
y) b |
2 |
|
|
|
2 |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
(x |
|
|
|
x c |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
(1 y) a2 (x y) b2 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2x y 0, |
|
|
x |
1 |
|
, y |
2 |
. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 2y 1 0 |
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Итак, MN |
|
1 |
|
|
|
a |
|
|
|
|
|
b |
|
|
|
c |
|
|||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
b |
|
|
c , |
|
|
MN |
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
c |
|
|
|||||||||||||||
3 |
|
3 |
3 |
|
|
3 |
3 |
3 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
3 |
|
. |
|
|
|
|
|
|
|
Ответ: |
|
|
|
3 |
|
|||||||||||||||||
|
|
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
9 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
метод опорных задач
Опорная задача
Если AB и CD – скрещивающиеся ребра треугольной пирамиды ABCD, d – расстояние между ними, АВ а, CD b,
– угол между AB и CD, V – объем пира-
миды ABCD, то d 6V . absin
Пример 25. В единичном кубе ABCDA1B1C1D1 найти расстояние меж-
ду диагональю куба BD1 и диагональю грани AB1 .
 C1
C1
B1 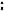 D1
D1
A1 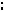


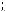 C
C
B D
D
A
Рис. 27
Решение. Найдем искомое расстояние
по формуле d |
|
|
|
6V |
, где V – |
|||||||||
|
AB1 BD1 sin |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
объем пирамиды |
|
ABB1D1 (см. рис. 27), |
||||||||||||
AB |
|
, |
BD |
|
|
|
, |
|
– угол меж- |
|||||
2 |
|
3 |
||||||||||||
|
|
|
||||||||||||
1 |
|
|
|
1 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
ду прямыми BD1 |
|
и AB1 . Так как площадь |
||||||||||||
основания |
АВВ1 |
пирамиды ABB1D1 рав- |
||||||||||||
на |
1 |
, а высота A D равна 1, то V |
1 |
. |
||||||||||
2 |
|
|
|
1 |
1 |
|
|
|
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
18.02.2011 |
15 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Следовательно, d |
|
1 |
|
|
|
1 |
|
. |
|||
|
|
|
|
|
|
|
|
||||
2 3 |
6 |
||||||||||
|
|
|
|
||||||||
Ответ: 1 .  6
6
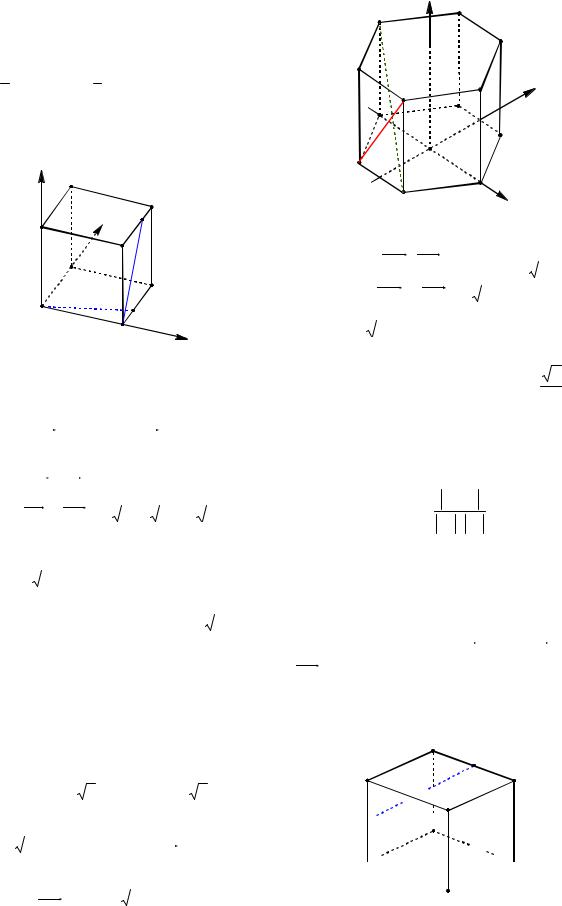
Пример 25. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны l, найти расстояние между прямыми AB1 и BC1.
Решение. Найдем синус угла между данными прямыми. Так как AB1 ||BM , то получим косинус угла из треугольника
MBC1 (см. рис. 28):
|
BM2 BC2 |
|
MC |
2 |
|
|
|
|
2 2 1 |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
cos |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
2 BM BC1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 4 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Рис. 28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда |
sin |
|
1 |
9 |
|
|
|
|
|
|
|
7 |
|
|
|
Расстояние |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отточки |
C до прямой |
A B |
|
|
равно |
|
|
|
|
3 |
|
|
. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||
Объем пирамиды ABB1C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
с основанием |
||||||||||||||||||||||||||||||||||||||||||||||||
ABB1 равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
V |
|
1 1 |
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
3 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Расстояние |
между |
|
|
прямыми |
|
AB1 и |
|||||||||||||||||||||||||||||||||||||||||||
BC1 равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
6 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
21 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18.02.2011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|||||
1.5.Угол между двумя прямыми
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
0 a, b 90 .
Углом между скрещивающимися пря-
мыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.
Две прямые называются перпендикулярными, если угол между ними равен 90 .
Угол между параллельными прямыми
считается равным нулю.
поэтапно-вычислительный метод
При нахождении угла между прямыми m и l используют формулу
cos | b2 c2 a2 | , 2bc
где a и b длины сторон треугольника АВС, соответственно параллельных этим прямым.
Пример 27. В кубе ABCDA1B1C1D1
найти угол между прямыми A1D и D1E ,
где E – середина ребра CC1.
Решение. Пусть F – середина ребра ВВ1, а – ребро куба, – искомый угол
(см. рис. 29).
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
||
|
|
A1 |
|
|
|
|
F |
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
D1 |
|
|
|
E |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 29 |
|
|
|
|
|
|
|
||
Так как |
A1F || D1E , то |
– |
угол при |
|||||||||||
вершине A1 |
|
|
в треугольнике A1FD. Из |
|||||||||||
треугольника BFD имеем |
|
|
|
|
|
|
|
|||||||
FD |
2 |
BD |
2 |
BF |
2 |
2a |
2 |
|
a2 |
|
9a |
2 |
, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
||
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
а из треугольника A1B1F получаем
A F |
2 |
A B |
2 |
B F |
2 |
a |
2 |
|
a2 |
5a |
2 |
|
||
|
|
|
|
|
|
|
|
|
, |
|||||
|
|
|
|
|
|
|
||||||||
1 |
|
1 |
1 |
|
1 |
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда A1F a 5 . 2
Далее в треугольнике A1FD используем теорему косинусов
FD2 A1D2 A1F2 2A1D A1F cos ,
|
9a |
2 |
2a |
2 |
|
|
5a2 |
2a |
|
|
a 5 |
|
|
|
|
||||
|
|
2 |
cos , |
||||||||||||||||
4 |
|
|
4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
откуда cos |
|
1 |
|
|
и arccos |
|
|
1 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
10 |
|
|
10 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: arccos 1 .
 10
10
Замечание. Для упрощения вычислений длину ребра куба удобно принять за единицу.
Пример 28. В правильной треугольной призме ABCA1B1C1 , ребра которой равны l, найти угол между прямыми AС1 и
B1С .
Решение. Проведем CM ||AC1 (см. рис. 30). Тогда
(AС1, B1C) (CM, B1C) .
B1
M C1 
A1
B
N
C
A
Рис. 30
Из треугольника MС1B1 с помощью теоремы косинусов находим
MB12 12 12 2 1 1 ( 0,5) 3.
Далее из треугольника MСС1 , используя теорему косинусов, получаем
cos |
2 |
2 3 |
|
|
1 |
и arccos |
1 |
. |
|||
|
|
|
|
|
|
|
|
||||
|
2 |
|
2 2 |
4 |
4 |
|
|||||
18.02.2011 |
|
|
|
|
|
|
|
|
17 |
||
Ответ: arccos1 . 4
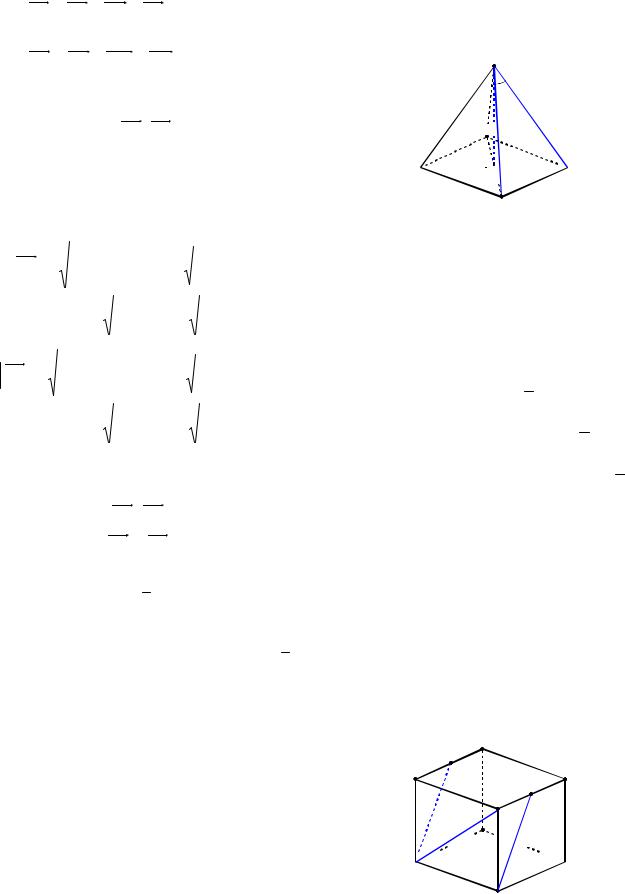
Пример 29. (МИОО, 2010). В пра-
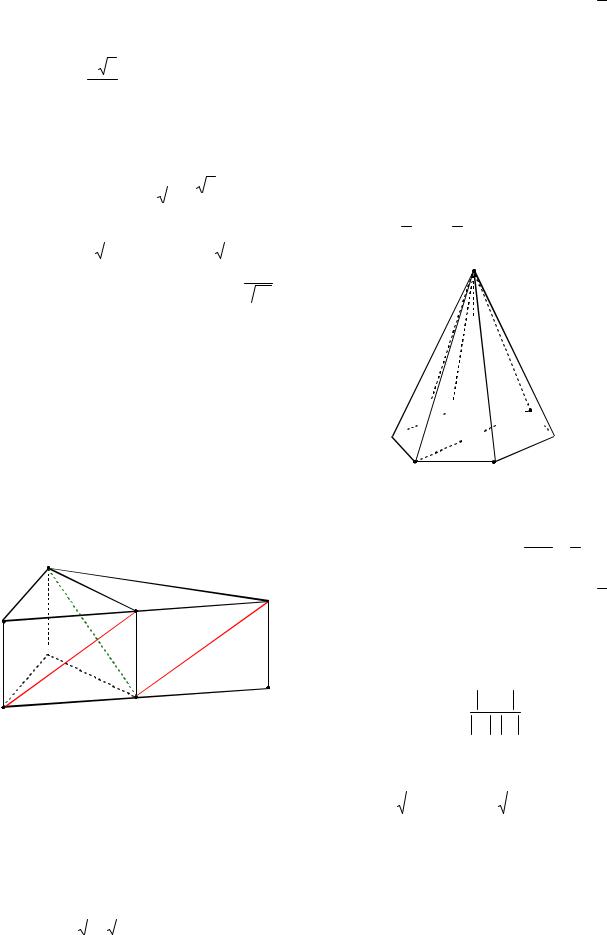
вильной шестиугольной пирамиде MABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найти косинус угла между MB и AD.
Решение. Прямая AD параллельна прямой BC (см. рис. 31). Следовательно, искомый угол MBC . В равнобедренном треугольнике MBC проведем апофему
ML, BL 1 BC 1 . 2 2
M
L


 C
C








 D
D


B



 E
E
A F
Рис. 31
Из прямоугольного треугольника
BML получаем cos MBL BL 1 .
BM 4
Ответ: 1 . 4
векторно-координатный метод
При нахождении угла между прямыми m и l используют формулу
p q cos p q
или в координатной форме:
cos |
|
|
|
x1x2 y1 y2 |
z1z2 |
|
|
|
, |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
y2 |
z2 |
x2 y |
2 |
z2 |
||||
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
|||
где p {x1, y1, z1} |
и q {x2, y2, z2} век- |
||||||||||
торы, соответственно параллельные этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы p q 0
или x1x2 y1 y2 z1z2 0.
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Пример 30. В единичном кубе ABCDA1B1C1D1 найти угол между прямыми АЕ и DF, где Е и F – точки, расположенные на ребрах CD и C1D1 так, что
DE 1 DC , C F 1C D . |
||||
3 |
1 |
3 |
1 |
1 |
Решение. Введем прямоугольную системукоординат, как указано на рисунке 32.
|
|
|
|
z |
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
A1 |
|
y |
|
|
|
|
F |
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
B |
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A |
|
|
|
|
D |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда А(0;0;0), D(1;0;0) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
, Е 1; |
|
|
;0 |
, |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
F 1; |
|
;1 |
, |
|
AE 1; |
|
|
;0 |
, DF |
0; |
|
|
|
;1 |
, |
|
|
|||||||||||||||||||||||
3 |
3 |
3 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
AE DF |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
cos |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
AE |
|
DF |
|
|
|
10 |
|
|
|
13 |
|
|
|
|
|
130 |
|
|
|
|
||||||||||||||||
arccos |
|
|
2 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
, где искомый угол. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
130 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arccos |
|
|
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
130 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 31. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны l, найти угол между прямыми AB1 и BF1 .
Решение. Введем прямоугольную системукоординат, как указано на рисунке 33.
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, B |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
; |
|
|
|
;0 |
|
|
; |
;1 |
||||||||||||||||||
Тогда А |
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
2 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
F 1;0;1 , |
AB 1;0;1 , |
|||||||||||||||||||||||
B |
; |
|
|
;0 |
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BF |
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
; |
|
;1 |
|
, |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18.02.2011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|||
F1 |
|
|
|
|
z |
|
E1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A1 |
|
|
|
|
|
|
C1 |
|
|
|
y |
|
|
|
|
|||||
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|||||
A |
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
B |
|
|
|
|
x |
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 33 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
AB1 BF1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
cos |
|
|
|
|
|
2 |
|
|
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
AB1 |
|
BF1 |
|
|
|
2 2 |
8 |
|
|
||||||||
|
|
|
|
, где искомый угол. |
||||||||||||||||
arccos |
|
2 |
||||||||||||||||||
|
|
|
||||||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: arccos 2 . 8
векторный метод
При использовании данного метода применяют формулу
p q cos p q .
Пример 32. В кубе ABCDA1B1C1D1
найти угол между прямыми EF и PQ, где E, F, P, Q – середины ребер DD1 , BC, AA1
и B1C1 соответственно.
Решение. |
Пусть |
AD a , |
AA1 c (см. |
рис. |
34), где |
|c | 1, a b a c b c 0.
B1
Q
A1



 D1
D1
AB b , |a | |b |
C1
P
 B
B
F
E





A


 C D
C D
Рис. 34
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
EF ED DC CF |
|
|
|
|
|
c b |
|
|
|
|
|
|
a, |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
PQ PA AB BQ |
|
|
|
|
c b |
|
|
|
|
|
a , |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
откуда находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PQ EF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
c b |
|
|
|
a |
|
|
|
|
|
|
c b |
|
|
|
a |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
b |
|
|
|
|
c |
|
|
|
|
|
|
a |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
4 |
|
|
4 |
|
4 |
4 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
1 |
|
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
PQ |
|
|
|
|
c b |
|
|
|
|
a |
|
|
|
|
|
|
|
|
c |
|
|
|
b |
|
|
|
|
|
|
|
a |
|
||||||||||||||||||||||||||||||
|
2 |
|
2 |
4 |
|
|
|
|
|
|
4 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
2 |
|
|
|
1 |
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
EF |
|
|
|
c b |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
b |
|
|
|
|
|
|
|
a |
|
|||||||||||||||||||||||||||||||
|
2 |
2 |
|
4 |
|
|
|
|
4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Подставляя |
|
|
полученные |
|
|
|
|
|
значения |
в |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
формулу, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
cos |
|
|
|
PQ EF |
|
|
|
|
1 |
|
: |
|
|
3 |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
PQ |
|
EF |
|
|
|
2 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда arccos1 , где искомый
3
угол.
Ответ: arccos1 . 3
метод опорных задач
● Применение теоремы «о трех косинусах»
Пример 33. Угол между боковыми ребрами правильной четырехугольной пирамиды, не лежащими в одной грани, равен 120 . Найти плоский угол при вершине пирамиды.
Решение. В правильной четырехугольной пирамиде SABCD проведем диагональное сечение ASC (см. рис. 35); SD – наклонная к плоскости сечения, SO
– высота пирамиды и проекция SD на эту
18.02.2011 |
19 |
плоскость, SC – прямая, проведенная в плоскости ASC через основание наклонной. По условию ASC 120 .
S
B

A






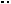 O
O









 C
C
D
Рис. 35
На основании теоремы о трех косинусах (опорная задача 3) имеем:
cos DSC cos DSO cos CSO.
Отсюда
cos DSC cos60 cos60
cos2 60 1 . 4
Следовательно, DSC arccos1 . 4
Ответ: arccos1 . 4
● Применение теоремы косинусов для трехгранного угла
Пример 34. В кубе ABCDA1B1C1D1
найти угол между прямыми AD1 и DM,
где М – середина ребра D1C1 .
Решение. Пусть ребро куба равно 1, точка N – середина ребра А1В1 , тогда ис-
комый угол равен углу между AD1 и
AN (см. рис. 36).
|
B1 |
A1 |
N |
C1 |
|
|
M |
|
D1 |


 B
B 


A





 C
C
D
Рис. 36
www.alexlarin.narod.ru
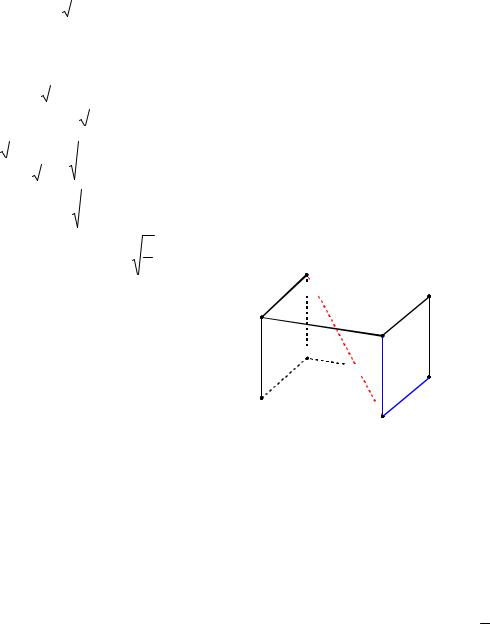
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Используем теорему косинусов для трехгранного угла с вершиной A (опорная задача 2), в котором A1 AD1 ,
A1AN , NAD1 . Так как в кубе все двугранные углы при ребрах прямые, то 90 . Тогда из теоремы следует,
что
cos cos cos .
Из |
прямоугольного |
треугольника |
||||||||||||||||||||||||||||||
A1 AD1 |
находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|||||
|
cos cos45 |
|
2 |
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
из треугольника A1AN получаем |
||||||||||||||||||||||||||||||||
|
|
AA1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
|||||||||||
|
cos |
|
|
1: |
5 |
|
|
|
||||||||||||||||||||||||
|
AN |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
5 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||
Отсюда cos |
|
|
|
2 |
|
|
|
2 |
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||
Следовательно, |
arccos |
|
|
2 |
|
. |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
5
Ответ: arccos 2 . 5
● Применение формулы cos2 cos2 cos2 1,
где , и – углы, которые образует некоторая прямая с тремя попарно перпендикулярными прямыми.
Пример 35. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Его диаго-
наль В1D составляет с ребром AD угол 45 , а с ребром DC угол 60 . Найти угол между прямыми В1D и DD1 .
Решение. Так как параллелепипед ABCDA1B1C1D1 прямоугольный, то его ребра, выходящие из одной вершины попарно перпендикулярны. Рассмотрим вершину D и воспользуемся данной выше формулой
cos2 cos2 cos2 1,
где ADB1 , CDB1 , D1DB1
(см. рис. 37).
B1

 C1
C1
A1
D1
B








 C
C
A
D
Рис. 37
Так как по условию 45 , 60 , то получаем
cos2 45 cos2 60 cos2 1,
cos2 1 |
1 |
|
1 |
|
1 |
. |
|
|
|
||||
4 |
2 |
4 |
|
|||
Поскольку – острый угол, то cos 1 . 2
Отсюда 60 .
Ответ: 60 .
18.02.2011 |
20 |
www.alexlarin.narod.ru
