
C2-2011
.pdf
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
C1
B1
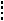
 D1
D1




 A1
A1


 C
C 





B








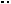





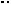




 D
D
 A
A
Рис. 57
Решение. Так как прямая B1D перпендикулярна проведенной плоскости (на рис. 57 эта плоскость изображена условно), а прямая CD AA1D1 (CD D1D так как призма и CD AD так как ABCD прямоугольник), то угол между рассматриваемыми плоскостями равен углу между прямыми B1D и CD.
Тангенс этого угла найдем из прямо-
угольного |
треугольника |
CB1D |
(CD AA1D1, |
следовательно |
CD B1C). |
Так как скрещивающиеся прямые A1C1 и BD лежат в параллельных плоскостях, то расстояние между ними равно расстоянию между этими плоскостями. Значит высота и боковое ребро призмы равны
|
|
|
BC2 BB |
2 |
|
||||
|
3. Тогда BC |
6 и ис- |
|||||||
1 |
1 |
|
|||||||
комый тангенс равен |
B1C |
|
6 |
|
1,2. |
||||
|
|
||||||||
|
|
|
|
CD 5 |
|
|
|||
Ответ: 1,2.
векторно-координатный метод
Применение данного метода позволяет свести решение исходной задачи к задаче о нахождении угла:
а) между векторами нормалей данных плоскостей;
б) между направляющими векторами скрещивающихся прямых а и b, лежащих в рассматриваемых плоскостях и перпендикулярных к их линии пересечения.
● использование векторов нормалей пересекающихся плоскостей
Любой ненулевой вектор, перпендикулярный плоскости – ее вектор нормали.
18.02.2011 |
31 |
Известно, что каждое уравнение пер-
вой степени |
px qy rz d 0 при усло- |
|||
вии |
p2 q2 r2 0 |
задает в прямоуголь- |
||
ной |
системе |
координат единственную |
||
плоскость, |
для |
которой |
вектор |
|
n {p, q, r} является вектором нормали. Задачу о нахождении угла между
плоскостями и |
, заданными уравне- |
||
ниями |
p1x q1y r1z d1 0 |
и |
|
p2x q2 y r2z d2 |
0 соответственно, |
||
удобнее свести к задаче о нахождении
угла между |
векторами |
их |
нормалей |
||||||||||||
n {p1, q1, r1} |
и n |
{p2, q2, r2}, исполь- |
|||||||||||||
зуя формулу |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
| n n | |
|
|
|
|
|
|
||||||
cos ( , ) |
| n | |n | |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
p1p2 q1q2 r1r2 |
|
|
|
|
. (1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p2 |
q2 r2 |
p2 q2 |
r2 |
||||||||||||
|
|
|
|||||||||||||
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
|
||||||
Пример 53. Найти угол между плос- |
|||||||||||||||
костями |
2x 3y 6z 5 0 |
и |
|||||||||||||
4x 4y 2z 7 0. |
|
|
|
|
|
|
|
|
|
||||||
Решение. |
Векторы |
n1 {2;3;6} |
и |
||||||||||||
n2 {4; 4; 2} – векторы нормалей плоскостей 2x 3y 6z 5 0 и 4x 4y 2z 7 0 соответственно.
Тогда по формуле (1) косинус угла между данными плоскостями равен:
|
|
|
n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cos |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n1 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
| 2 4 3 4 6 2| |
|
|
|
16 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
4 9 36 |
16 16 4 21 |
|||||||||||||
Отсюда arccos |
16 |
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
16 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arccos |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|||||
Пример 54. В кубе |
ABCDA1B1C1D1 |
|||||||||||||||||||||
найти угол между плоскостями |
AB1C и |
|||||||||||||||||||||
BC1D . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
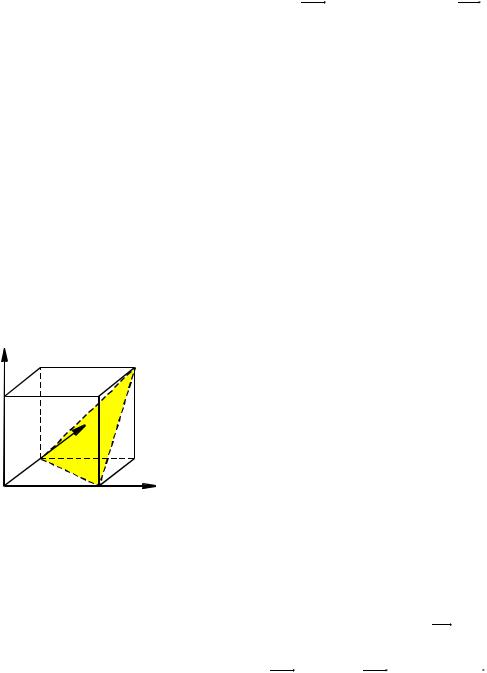
Решение. |
Пусть |
|
AD a , |
AB b , |
||||||||||||||||||
AA1 c |
|
|
(см. |
|
|
рис. |
58), |
где |a | |b | |
||||||||||||||
| c | 1, a b a c b c 0.
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
B1
A1 |
C1 |
 D1
D1


B

A
















 C
C
D
Рис. 58
Векторы BD1 и CA1 являются векто-
рами нормали плоскостей AB1C и BC1D
соответственно, так как BD1 AB1C и CA1 BC1D. Тогда
BD1 a b c , CA1 a b c , BD1 CA1 (a b c)( a b c)
a2 b2 c2 1,
|
BD |
|
(a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
b c)2 |
a2 b2 c2 3 , |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
( a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
b c)2 |
a2 b2 c2 3 , |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
BD1 CA1 |
|
|
1 |
|
|
|
1 |
. Откуда |
|||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
BD1 |
|
|
CA1 |
|
|
3 |
3 3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccos1 , где искомый угол. 3
Ответ: arccos1 . 3
Пример 55. В правильной пирамиде MABCD (M вершина) высота и сторона основания равны 4. Точка F середина ребра MC . Плоскость проходит через середину ребра AM перпендикулярно прямой BF . Найти угол между: а) плоскостью и плоскостью основания; б) плоскостью и прямой DM .
Решение. Так как прямая BF , то
ее направляющий вектор BF является вектором нормали плоскости (см. рис. 59). Точка O основание высоты MO,
следовательно, вектор OM является вектором нормали плоскости ABC. Тогда получим
cos ( , ABC) |
| BF OM | |
. (*) |
|
||
|
| BF| |OM | |
|
Соответственно, для нахождения угла между прямой DM и плоскостью воспользуемся формулой:
sin ( , DM) |
| BF DM | |
. |
(**) |
|
|||
|
| BF| | DM | |
|
|
Введем систему координат Oxyz |
сле- |
||
дующим образом. Пусть начало координат находится в центре основания в точке O, ось x проходит через точку O параллельно ребру AD, ось y проходит через точку O параллельно ребру AB , ось z проходит через точку O перпендикуляр-
но плоскости |
основания |
(см. рис. 59). |
|
z |
|
|
M |
|
|
B |
F y |
|
|
|
A |
O |
C |
|
D |
x |
Рис. 59
Найдем координаты точек и векторов:
O(0;0;0), B( 2;2;0), C(2; 2;0), M(0;0;4), F(1;1; 2), D(2; 2;0).
Тогда
BF {3; 1; 2}, | BF | 
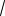 9 1 4
9 1 4 
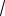 14 ,
14 ,
OM {0;0;4}, |OM | 4,
DM { 2; 2; 4}, | DM | 
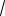 4 4 16 2
4 4 16 2
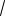 6 .
6 .
Используя формулы (*) и (**), получим
cos ( , ABC) |
| 3 0 ( 1) |
0 2 4| |
|
|
2 |
|
, |
|
|
|
|
|
|
|
|||
|
14 4 |
14 |
|
|
||||
sin ( ,DM) |3 ( 2) ( 1) 2 2 4| 0. 
 14 2
14 2
 6
6
Ответ: ( , ABC) arccos 2 ,  14
14
( ,DM) 0.
18.02.2011 |
32 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Приведем один из способов получения уравнения плоскости, если известны координаты трех ее точек M(xM , yM , zM ),
N(xN , yN , zN ), P(xP , yP, zP ), не лежащих на одной прямой. Для этого нужно взять в общем виде уравнение плоскости ax by cz d 0, в котором a,b, c, d –
неизвестные числа. Подставив в него координаты точек M, N, P, получим систему уравнений:
axM byM czM d 0,axN byN czN d 0,
axP byP czP d 0.
Решив ее, найдем a pd,b qd, c rd
(если окажется, что |
d 0, то |
a pc, |
b qc; если d c 0, |
то a pb). Под- |
|
ставив в исходное уравнение и сократив на d 0, получим уравнение
px qy rz 1.
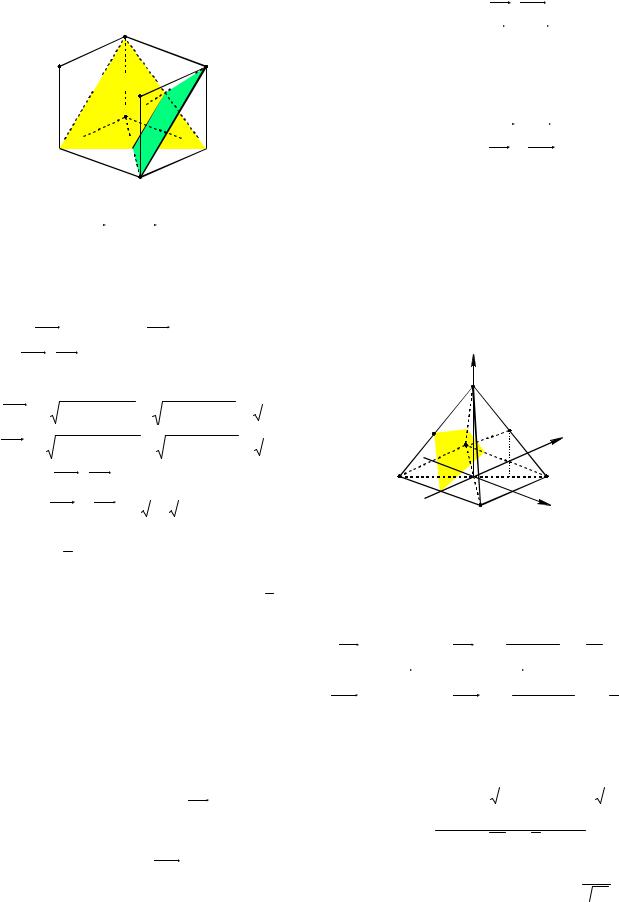
Выведем, например, в выбранной системе координат уравнение плоскости, проходящей через точки B, D и C1 (см.
рис. 60), если ребро куба равно 1.
z |
B1 |
|
C1 |
A1 |
|
D1 |
|
|
|
|
|
|
|
y |
|
|
B |
|
C |
A |
|
D |
x |
|
|
Рис. 60 |
|
Для этого выразим координаты точек:
B(0;1;0), D(1;0;0), C1(1;1;1). Записав в
общем виде уравнение плоскости ax by cz d 0 и подставив в него координаты этих точек, получим:
a 0 b 1 c 0 d 0, |
(для точки B) |
|
(для точки D) |
a 1 b 0 c 0 d 0, |
a 1 b 1 c 1 d 0. (для точки С1)
Отсюда b d, a d и c d . Уравне-
ние плоскости BC1D имеет вид
18.02.2011
dx dy dz d 0 или x y z 1 0
после сокращения на d 0.
В задачах на вычисление угла между пересекающимися плоскостями в общем случае уравнение плоскости находить не требуется. Координаты вектора нормали можно вывести, если известны координаты трех точек плоскости M, N, P, не лежащих на одной прямой. Для этого нахо-
дим координаты двух векторов плоскости a MN {a1, a2, a3} и b MP {b1, b2, b3}.
Предположим, что вектор с координатами n {p, q, r} (здесь p, q, r – неизвестные числа, которые нужно найти) перпендикулярен любому вектору плоскости
, т.е. a и b в том числе. Его координаты ищутся из условий равенства нулю скалярных произведений n с векторами
a и b из следующей системы уравнений:
n a 0, |
a p a q a r 0, |
||
|
1 |
2 |
3 |
|
|
|
|
n b 0; |
b1 p b2q b3r 0. |
||
|
|
|
|
Эта система имеет бесконечное множество решений, так как векторов, перпендикулярных плоскости , бесконечно много. Выразив, например, из системы координаты p и q через r, выберем не-
нулевой вектор n {p(r);q(r); r}, взяв в качестве r какое-нибудь число (обычно берут так, чтобы в координатах не было дробей или радикалов).
Пример 56. В единичном кубе ABCDA1B1C1D1 найти угол между плос-
костями AD1E и D1FC, где точки Е и F
– середины ребер А1В1 и В1С1 соответственно.
Решение. Введем прямоугольную системукоординат, как указано на рисунке61.
Тогда |
А(0;0;0), |
|
С(1;1;0), |
|
D1(1;0;1), |
||||||||
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|||
Е 0; |
|
;1 |
, F |
|
;1;1 |
, |
AE 0; |
|
|
;1 |
, |
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|||
АD1 {1;0;1}, СD1 {0; 1;1}, СF |
|
|
|
1 |
|
||||||||
|
|
|
;0;1 . |
||||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем вектор n {x, y, z}, перпенди-
кулярный плоскости AD1E. Этот вектор
33
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
должен быть перпендикулярным векто-
рам AE и АD1 , поэтому
|
|
|
|
y |
z 0 |
y 2z |
||||
n AE 0 |
|
|
2 |
|
||||||
|
АD 0 |
|
|
|
|
|
|
|||
n |
|
|
|
|
|
|
x z. |
|||
|
|
1 |
|
x z 0 |
|
|
||||
|
|
z |
B1 |
|
|
F |
|
|
|
|
|
|
|
E |
|
|
|
C1 |
|
||
|
|
|
|
|
|
|
|
|||
|
|
A1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
y |
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
A |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 61 |
|
|
|
||
Пусть |
z 1, |
тогда |
x 1, |
y 2 и |
||||||
n {1; 2; 1}. Найдем вектор m {x, y, z},
перпендикулярный плоскости D1FC . Этот вектор должен быть перпендикуляр-
ным векторам CD1 |
и CF , поэтому |
|
|||||||||||||
|
|
|
|
|
|
|
|
y z 0, |
y z, |
||||||
m CD 0, |
|||||||||||||||
|
1 |
|
|
|
|
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
x 2z. |
||||||
|
|
|
|
|
|
|
|
|
|
|
z 0 |
|
|||
|
|
|
|
|
|
|
|
||||||||
m CF 0 |
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть z 1, |
тогда |
x 2, |
y 1 и |
||||||||||||
m {2;1;1}. |
Для |
|
нахождения |
искомого |
|||||||||||
угла |
|
|
|
|
используем |
формулу |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos |
|
|
n m |
|
. Так как |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
n |
|
m |
|
|
|
|
|
|
|
|
|||
n m 1 2 2 1 ( 1) 1 3, | n| 
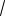 6 ,
6 ,
| m|  6 , то cos 0,5, откуда 60 .
6 , то cos 0,5, откуда 60 .
Ответ: 60 .
Пример 57. Дан куб ABCDA1B1C1D1 .
Найти угол между плоскостями MNP и AKD, где точки M – центр грани AABB1 1 ,
N – середина ребра B1C1 , K – середина ребра CC1 , P – делит ребро DD1 в от-
ношении DP:PD1 1:2.
Решение. Введем систему координат следующим образом. Точку A примем за
18.02.2011
начало координат. Оси Ax , Ay и Az на-
правим вдоль ребер куба AD, АВ и AA1 соответственно (см. рис. 62). Пусть ребро куба равно 1. Выразим координаты точек:
A(0;0;0), |
D(1;0;0), |
K(1;1;0,5), |
|
||||||||||||||||
|
1 |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|||||||
M |
0; |
|
|
; |
|
|
|
, |
M |
|
;1;1 , |
P 1;0; |
|
|
. |
||||
|
|
2 |
|
|
|||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
3 |
|
||||||||
|
|
|
|
z |
|
|
B1 |
|
|
N |
|
C1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
A1 |
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|||
|
|
|
|
|
|
M |
|
|
|
y |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
B |
|
|
|
C |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A |
|
|
|
|
|
D |
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 62 |
|
|
|
|
|
|
|
|||
Найдем координаты векторов: |
|
|
|
|
|||||||||||||||
|
1 |
1 |
|
1 |
|
|
|
|
|
1 |
|
1 |
|||||||
MN |
|
; |
|
|
; |
|
, MP |
1; |
|
; |
|
|
|
||||||
|
|
|
|
2 |
2 |
|
|
||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
6 |
|||||||||
AD {1;0;0}, AK {1;1;0,5}.
Теперь найдем координаты векторов n1 и n2 , перпендикулярных плоскостям MNP и AKD соответственно. Начнем с вектора n1 {p1, q1, r1}. Его координаты ищутся из условий равенства нулю скалярных произведений n1 с векторами
MN и MP . Получаем систему
n |
MN 0, |
0,5p1 |
0,5q1 0,5r1 |
0, |
||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
n |
MP 0; |
p1 0,5q1 |
|
|
r1 |
0; |
|
|||||
|
|
|
||||||||||
|
1 |
|
|
|
6 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
p |
2 |
r , q |
7 |
r . |
|
|||||
|
|
|
|
|
||||||||
|
|
1 |
9 1 |
1 |
9 |
1 |
|
|
||||
Эта система имеет бесконечное множество решений, так как векторов, перпендикулярных плоскости MNP, бесконечно много. Выберем из данного мно-
жества ненулевой |
вектор n1 , |
положив |
|
r1 |
9. Тогда n1 { 2; 7;9}. |
|
|
|
Найдем теперь |
координаты |
вектора |
n2 |
{p2, q2, r2}, |
перпендикулярного |
|
плоскости AKD. Его координаты ищутся из условий равенства нулю скалярных
произведений n2 с векторами AD и AK .
34
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
Получаем систему
n AD 0, |
|
p |
2 |
0 q |
2 |
0 r 0, |
|
||
2 |
|
|
|
|
2 |
|
|||
|
|
q2 0,5r2 |
0; |
||||||
n AK 0; |
|
p2 |
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
p2 |
0, q2 0,5r2. |
|
|
|||||
Возьмем r2 2. Тогда n2 {0; 1; 2}. Для нахождения угла между плоско-
стями MNP и AKD воспользуемся форму-
лой (1):
cos (MNP, AKD)
|
|
|0 7 18| |
|
|
125 |
. |
||
|
|
|
|
|
|
|||
|
|
4 49 81 0 1 4 |
134 |
|
||||
Отсюда (MNP, AKD) arccos 125. 134
Ответ: arccos 125. 134
● использование направляющих векторов скрещивающихся прямых
Ненулевой вектор q называется направляющим вектором прямой l, если он лежит либо на самой прямой l, либо на прямой, параллельной ей.
Пусть p {x1, y1, z1} и q {x2, y2, z2}
– направляющие векторы прямых а и b, тогда угол между этими прямыми (пересекающимися или скрещивающимися) находят по формуле:
cos |
|
|
|
x1x2 y1y2 |
z1z2 |
|
|
|
. (2) |
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
y2 |
z2 |
|
x2 |
y2 |
z2 |
||||
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
||||
Пример 58. В основании пирамиды MABCD лежит прямоугольник с отношением сторон AB: AD 1:2 (см. рис. 63). Каждое боковое ребро наклонено к плоскости основания под углом, равным 60 . Точка R – середина ребра MC . Найти угол между плоскостями MAC и ADR.
Решение. Если считать, что AB a, тогда AD 2a, и все линейные элементы в пирамиде будут зависеть от одного параметра а. Поэтому, не теряя общности, с точностью до подобия можно принять AB 4. Тогда AD 8, OM 2
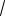 15, где
15, где
О – точка пересечения диагоналей прямоугольника, лежащего в основании.
Вершина M пирамиды MABCD проектируется в точку O. Введем систему координат следующим образом. Точку O примем за начало координат. Оси Ox и Oy направим параллельно сторонам основания, а ось Oz вдоль высоты пирамиды OM .
z
|
M |
|
|
Q |
R |
y |
|
H |
|||
|
C |
||
B |
|
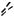



 O
O


 x
x
A D
Рис. 63
Выразим координаты точек:
A( 4; 2;0), |
B( 4;2;0), C(4;2;0), |
D(4; 2;0), M(0;0;2
 15), R(2;1;
15), R(2;1; 
 15).
15).
Отрезок AR является высотой в равностороннем треугольнике АМС, поэтому прямая МR перпендикулярна ребру AR искомого двугранного угла. Проведем в треугольнике ADR высоту DH. Тогда задача сведется к нахождению угла между прямыми МR и DH.
Найдем координаты векторов:
MR {2;1; 15}, AR {6;3; |
15}, |
|
||||
|
DA { 8; 0; 0}. |
|
|
|
||
Так как векторы AH и AR коллине- |
||||||
арны, |
то AH k AR {6k,3k, |
|
k}. |
|||
15 |
||||||
Далее из равенства DH DA AH полу- |
||||||
чаем |
DH {6k 8;3k; |
|
k}. Теперь, ис- |
|||
15 |
||||||
пользуя условие DH AR, имеем урав- |
||||||
нение |
6(6k 8) 9k 15k 0. |
Отсюда |
||||
k 0,8 и DH { 3,2; 2,4; 0,8
 15}.
15}.
Так как MR и DH – направляющие векторы прямых МR и DH соответственно, то для нахождения угла между этими прямыми воспользуемся формулой (2):
18.02.2011 |
35 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
cos |
|
|
6,4 2,4 12 |
|
|
1 |
. |
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
4 1 15 10,24 5,76 9,6 |
2 |
|
||||||||
|
|
|
||||||||
Значит, угол между прямыми МR и DH, и угол между данными плоскостями
равен . 4
Ответ: . 4
метод опорных задач
Используем следующие опорные задачи (теоремы):
а) теорема о площади ортогональной проекции многоугольника;
б) теорема «косинусов для трехгранного угла»;
в) теорема «о трех синусах»; г) формулы, выражающие синус или
косинус искомого угла через расстояния от точки до плоскости и до прямой.
● применение теоремы о площади ортогональной проекции многоугольника
При применении этого метода угол между плоскостями и можно вычислить, используя формулу
cos |
Sпр |
, |
(3) |
|
|||
|
S |
|
|
где S – площадь многоугольника, лежащего в плоскости , Sпр – площадь его ортогональной проекции на плоскость .
Пример |
59. В |
кубе |
|
|
ABCDA1B1C1D1 |
|||||||||||
найти угол между плоскостью грани |
||||||||||||||||
AA1B1B и плоскостью BC1D. |
|
|
|
|
|
|||||||||||
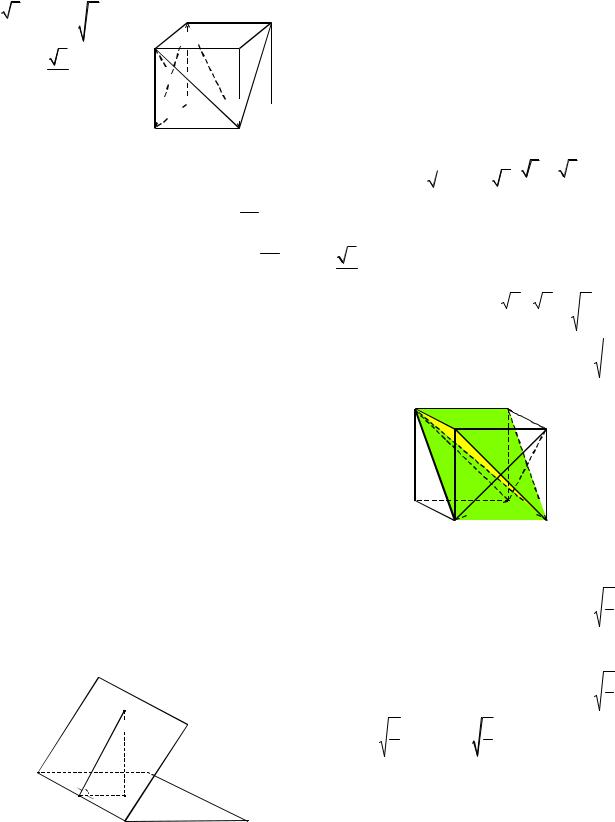
Решение. Пусть ребро куба равно 1. |
||||||||||||||||
Ортогональной проекцией |
|
треугольника |
||||||||||||||
BC1D на плоскость AA1B1 |
|
является тре- |
||||||||||||||
угольник AB1B (см. |
рис. |
|
64), площадь |
|||||||||||||
которого |
равна |
|
|
0,5. |
|
|
Поскольку |
|||||||||
BD BC1 C1D |
|
|
(как |
диагонали |
||||||||||||
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
. Из формулы |
||||||||
граней куба), |
то SBC D |
|
|
|
|
3 |
||||||||||
|
2 |
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SAB B |
|
|
|
|
|
|||
cos (AAB , BC D) |
|
|
3 |
. |
||||||||||||
|
|
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
1 |
1 |
1 |
|
|
|
|
SBC D |
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
18.02.2011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
Отсюда (AAB , BC D) arccos |
3 |
. |
||
|
||||
1 |
1 |
1 |
3 |
|
|
|
|
|
|
B1 C1
A1 D1
D1
|
|
|
B |
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис. 64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
Ответ: arccos |
|
3 |
||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 60. |
В |
кубе |
ABCDA1B1C1D1 |
|||||||||||||||||||||||
найти угол между плоскостями |
AB1C и |
|||||||||||||||||||||||||
АВС. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Пусть искомый угол. Ис- |
||||||||||||||||||||||||||
пользуем соотношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
SABC |
SAB C cos , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|||
где SABC |
|
, |
|
SAB C |
2)2 |
3 |
|
|
3 |
|||||||||||||||||
2 |
|
|
4 |
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(треугольник AB1C равносторонний) (см. |
||||||||||||||||||||||||||
рис. 65). Отсюда имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
: |
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cos |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следовательно, arccos 3 . 3
B1
A1 C1
C1
 D1
D1

 B
B
A




 C
C
D
Рис. 65
Ответ: arccos 3 . 3
Обычно рассматриваемый в этом пункте метод применяют при вычислении угла между плоскостью сечения и плоскостью какой-либо грани много-
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
гранника (часто в качестве такой грани выступает основание пирамиды или призмы). Так поступают в случаях, когда нахождение Sпр и Sсечения является более простой задачей, чем непосредственное вычисление двугранного угла , сопряжённое с построением на чертеже его линейного угла.
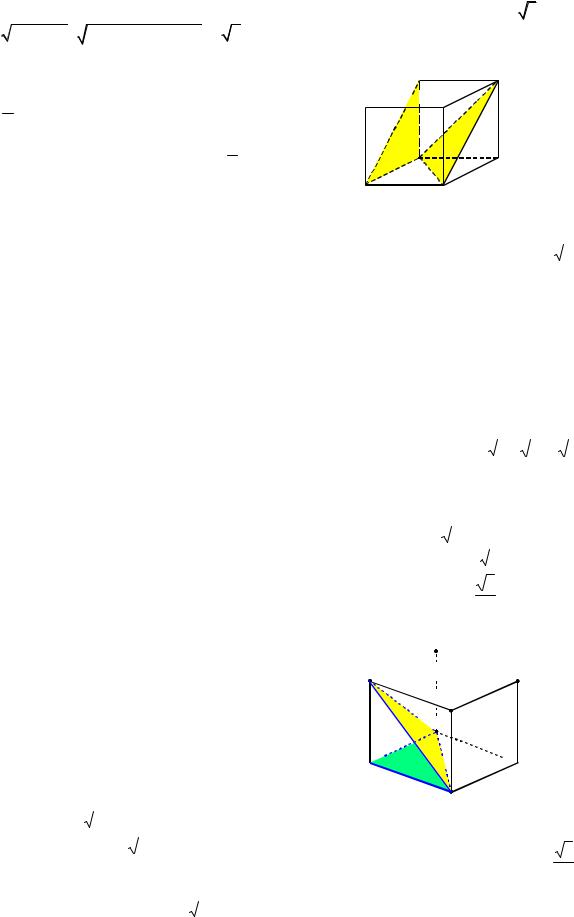
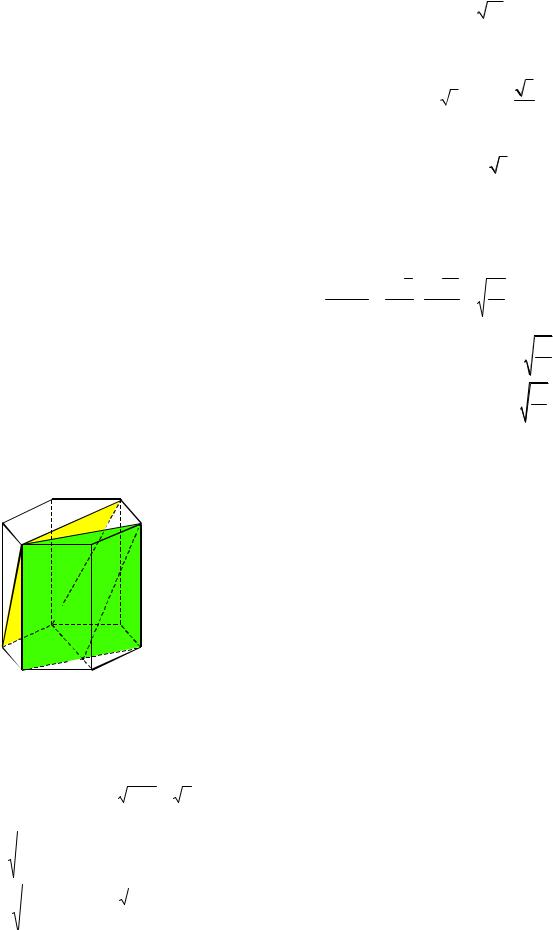
Пример 61. В правильной шестиугольной призме ABCDEFABC1 1 1DE1 1F1,
стороны основания которой равны 1, а боковые ребра равны 2, найти угол между плоскостями BAD1 1 и AAE1 1.
Решение. Заметим, что четырехугольники BADC1 1 и AAE1 1E сечения данной призмы плоскостями BAD1 1 и AAE1 1 (см.
рис. 66). Так как BA, DE1 1 и CF перпен-
дикулярны плоскости AAE1 1 (они пер-
пендикулярны AA1 и AE ), то трапеция
AAEG1 1 , где G середина отрезка AE ,
есть ортогональная проекция трапеции BADC1 1 на плоскость сечения AAE1 1E.
а площадь равна
SBA D C |
|
AD BC |
h |
3 19 |
. |
|
1 1 |
|
|||||
|
4 |
|||||
1 |
1 |
2 |
|
|
||
|
|
|
|
|
||
В прямоугольной трапеции AAEG1 1
основания равны A1E1 
 3, AG 3 , а 2
3, AG 3 , а 2
высота AA1 2. Ее площадь равна
S |
|
|
|
AE AG |
AA |
3 |
3 |
|
|
AA E G |
|
1 1 |
|
|
|
. |
|||
|
|
|
|||||||
|
2 |
1 |
|
|
2 |
|
|||
|
1 |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
В соответствии с формулой (3) находим:
cos (BA1D1, AA1E1)
SAA1E1G 3
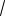 3 : 3
3 : 3
 19 12 .
19 12 .
SBA1D1C 2 4 19
Значит, искомый угол равен arccos 12 . 19
Ответ: arccos 12 . 19
C1 |
D1 |
B1 |
E1 |
A1 |
F1 |
C |
D |
B |
E |
|
G |
A |
F |
Рис. 66
Трапеция BADC1 1 равнобедренная, с
основаниями AD1 1 2, BC 1 и боковы-
ми сторонами BA1 CD1 |
1 4 5. Ее |
||||||||||||||||
высота h равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
h |
CD2 |
|
AD BC 2 |
|
|||||||||||||
|
|
1 |
1 |
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 1 |
2 |
|
|
|
|
|
|
|
||||||
|
|
5 |
|
19 |
|
|
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18.02.2011 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
● применение «теоремы косинусов для трехгранного угла»
Пример 62. В правильной треугольной призме ABCABC1 1 1 все стороны равны 1.
Найти косинус угла между плоскостями
ABC1 и ABC1 1 .
Решение. |
Рассмотрим |
|
трехгранный |
||||||||||||||||||||||||||||||||||||||||||
угол при вершине B пирамиды |
AACB . |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
||||
B1 |
|
|
|
|
|
|
C1 |
Обозначим |
через |
||||||||||||||||||||||||||||||||||||
|
|
A1 |
|
|
|
|
|
плоский |
|
|
|
|
угол |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
двугранного |
|
|
|
|
угла |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ABCA |
|
|
|
|
|
(см. |
|
|
|
|
рис. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
D |
|
|
|
|
|
|
|
|
67). Найдем зна- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
чения |
|
|
синусов |
и |
|||||||||||||||||||||||||||||||
B |
|
|
|
|
|
|
C |
косинусов |
|
|
|
|
|
|
|
|
|
|
|
пло- |
|||||||||||||||||||||||||
|
|
A |
|
|
|
|
ских |
|
|
|
|
углов |
|
|
|
|
при |
||||||||||||||||||||||||||||
|
|
|
|
|
|
вершине |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1. |
||||||||||||||||||||||||
|
|
Рис. 67 |
|
|
|
|
Грань ABB1A1 – |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||
квадрат, поэтому |
|
cos AB A |
2 |
В |
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ABC |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
треугольнике |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC 1, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB1 B1C |
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
cos ABC |
AB2 |
BC2 |
AC2 |
3 |
, |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 AB BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
sin ABC |
1 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В |
треугольнике |
|
|
|
B AC |
|
|
|
|
|
|
|
B A 1, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||||||||||||
AC BC |
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos CB1A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
2 1 2 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||
|
B1C2 B1A1 A1C |
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
2 B1C B1A1 |
|
|
|
|
|
2 |
|
2 1 2 2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||
|
|
sin CB A 1 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Применяя теорему косинусов для трехгранного угла (опорная задача 2) при вершине B1, получим
cos
cos AB1A1 cos AB1C cos CB1A1 5.
sin AB1C sin CB1A1 |
7 |
|
|
|
Ответ: |
5 |
. |
|
|
||
|
7 |
|
|
18.02.2011 |
38 |
||
● применение теоремы «о трех синусах»
Пример 63. В кубе ABCDA1B1C1D1
найдите угол между плоскостями AB1C и АВС.
Решение. Пусть искомый угол. Так как B1AC 60 , B1AB45 (см. рис. 68), то по теореме «о трех синусах» (опорная задача 4) имеем:
sin45 sin sin60 ,
sin 
 2 :
2 : 
 3
3 
 2 . 2 2
2 . 2 2  3
3
Отсюда arcsin 2 .  3
3
B1 C1
A1



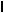 D1
D1 
B







 C
C
A D
Рис. 68
Ответ: arcsin 2 . 3
Пример 64. Диагональ A1C куба
ABCDA1B1C1D1 служит ребром двугранного угла, грани которого проходят через B1 и D1. Найти величину этого угла.
Решение. Будем считать куб единичным. Пусть Е – середина отрезка A1D,
тогда из треугольника A1D1E получаем
sin sin |
|
|
2 |
|
|
|
|
|
|||||
4 |
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
( – угол между прямой |
A1D1 и плоско- |
||||||||||||
стью A1B1C ) (см. рис. 69). |
|
|
|
|
|
|
|||||||
Из треугольника A1D1C находим |
|||||||||||||
|
CD1 |
|
|
|
|
|
|
|
|
|
, |
||
sin |
|
2 |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|||||||
|
CA1 |
3 |
|
3 |
|
|
|||||||
www.alexlarin.narod.ru
Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
где – угол между прямой A1D1 и реб-
ром A1C двугранного угла. Далее имеем
2 |
sin |
2 |
, |
|
2 |
3 |
|||
|
|
sin 3 . 2
Так как точка Е (проекция точки D1 на плоскость A1B1C )
A1 B1 D1 
 C1
C1
E

 A
A




 B D C
B D C
Рис. 69
расположена вне
искомого двугранного угла, то 2 . 3
Ответ: 2 . 3
● использование расстояний от точки до плоскости и до прямой
Решение задач этого пункта основано на применении таких понятий, как расстояние от точки до прямой и расстояние от точки до плоскости.
Пусть даны две плоскости и (см. рис. 70), пересекающиеся по прямой l. Если известны расстояния от точки М, лежащей в плоскости , до плоскости и до прямой l, то угол между плоскостями и можно вычислить, используя формулу
sin ( , ) |
(M, ) |
, |
(4) |
|
|||
|
(M,l) |
|
|
где (M, ) – расстояние от точки М до плоскости , M,l – расстояние от
точки М до прямой l.
M

Пример 65. В кубе ABCDA1B1C1D1
найти угол между плоскостями AB1C и A1B1C .
Решение. Пусть сторона куба равна 1. Плоскости AB1C и A1B1C пересекаются по прямой B1C (см. рис. 71). Расстояние от точки А, принадлежащей плоскости AB1C , до прямой B1C равно длине высо-
ты равностороннего треугольника AB1C
со стороной |
|
, т.е. |
|
|
3 |
|
6 |
. Рас- |
|
2 |
2 |
||||||||
2 |
2 |
||||||||
|
|
|
|
|
|
|
стояние от точки А до плоскости A1B1C равно половине диагонали квадрата, т.е.
2 . По формуле (4) имеем
2
sin (ABC, ABC) |
2 |
: |
6 |
|
1 |
. |
|
|
|
|
|||
|
|
|
|
|
|
||||||||
1 |
1 |
1 |
2 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда искомый угол равен arcsin |
1 |
. |
|||||||||||
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
B1 |
|
A1 |
C1 |
D1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
B 

 C
C
A D
D
Рис. 71
Ответ: arcsin 1 . 3
Замечание. Отметим, что в зависимости от способа решения ответ получа-
ется в разной форме: arcsin 1 , 3
arccos 2 или arctg 1 . 3 2
Рис. 70
18.02.2011 |
39 |
www.alexlarin.narod.ru

Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.
2.Площади и объемы
Вданном разделе требуется не только знание формул для вычисления площадей поверхностей и объемов многогранников, но и знание свойств пространственных фигур (призма и пирамида), признаки и свойства, которые относятся к взаимному расположению прямых и плоскостей
2.1. Площадь поверхности многогранника
Формулы для вычисления площади поверхности призматических тел
Боковая и полная поверхность прямой призмы
Sбок l P ,
где l длина бокового ребра, P – периметр основания, Sосн – площадь основания,
Sполн Sбок 2Sосн .
Боковая и полная поверхность наклонной призмы
Sбок l P ,
где l длина бокового ребра, P – периметр перпендикулярного ему сечения.
Sполн Sбок 2Sосн
Полная поверхность прямоугольного параллелепипеда
Sполн 2(ab bc ac) ,
где a,b, c – длины ребер, выходящих из одной вершины.
Формулы для вычисления площади поверхности n-угольной пирамиды
Боковая поверхность правильной пирамиды
1
Sбок 2 P a,
где P – периметр основания правильной пирамиды, a – апофема боковой грани;
S |
бок |
|
Sосн |
, |
|
|
|||||
|
|
cos |
|||
где Sосн – площадь основания, – мера дву- |
|||||
гранного угла при ребре основания. |
|||||
|
|
|
|
||
18.02.2011 |
|
40 |
|||
Боковая и полная поверхность правильной усеченной пирамиды
1
Sбок 2 (P1 P2) a,
где P1 и P2 – периметры верхнего и нижнего оснований, a – апофема боковой грани;
Sбок S1 S2 ,
cos
где S1 и S2 – площади верхнего и нижнего оснований, – мера двугранного угла при ребре нижнего основания;
Sполн Sбок S1 S2 .
Полная поверхность правильного тетраэдра
Sполн a2 
 3, где a – сторона.
3, где a – сторона.
Рассмотрим следующие задачи данного раздела: вычисление площади поверхности многогранника и его частей, нахождение линейных и нелинейных величин многогранника с известной площадью поверхности (части поверхности), сравнение площадей, сравнение отрезков.
поэтапно-вычислительный метод
Пример 66. В правильной четырехугольной призме диагональ равна d и наклонена к плоскости боковой грани под углом . Найти площадь боковой поверхности призмы.
Решение. Рассмотрим призму ABCDA1B1C1D1, для которой диагональ
AC1 d (см. рис. 72).
C1
B1


 D1
D1


 A1
A1
C

B

 D
D
 A
A
Рис. 72
www.alexlarin.narod.ru
