C2-2011

введение нескольких вспомогательных элементов

Пример 82. Найдите объем прямоугольного параллелепипеда, диагональ которого равна 14, периметр основания – 20 и периметр меньшей боковой грани –

32.

Решение. Пусть в параллелепипеде

Получаем квадратное уравнение

3b2 52b 160 0,

имеющее корни 4 и 40 (не удовлетворя-

метод опорных задач

● Объемы пирамид с общей высотой пропорциональны площадям ихоснований.

Пример 83. В правильной четырехугольной пирамиде SABCD точка F делит ребро ВС в отношении 1:3 (считая от точки С). Найдите, в каком отношении делит объем пирамиды плоскость

DSF ?

S

B

AFC

D

Рис. 87

Решение. Так как данная пирамида и части, на которые она разбивается плоскостью сечения (см. рис. 87), имеют одинаковую высоту, то отношение объемов

частей равно отношению площадей оснований:

VSABFD SABFD .

VSFCD SFCD

Площади треугольников ABD и BDC равны. Для треугольников с общей высотой имеем

SDCF CF 1 .

SDBF BF 3

Поэтому SABFD 7 .

SFCD 1

Ответ: 7:1.

● Объемы пирамид с равновеликими основаниями пропорциональны проведенным к нему высотам.

Например, в кубе ABCDA1B1C1D1 (см.

рис. 88) объемы пирамид A1 ABD и MBDC относятся как 2:1, где М – середина ребра C1C .

B1

A1 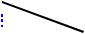C1

D1

BM

AC

D

Рис. 88

● Пирамиды с равновеликими основаниями и равными высотами – равновелики.

Например, в кубе ABCDA1B1C1D1 (см.

B DB DB D A A A

Рис. 89

D

B

CGHF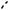

A

O

Рис. 91

Пример 85. На ребрах АВ, BD и DC пирамиды ABCD взяты точки M, L и K

DK 2 DC . В каком отношении плос-

5

кость KLM делит отрезок, соединяющий середины ребер AD и ВС?

Решение. Обозначим середины AD и ВС через P и Q соответственно (см. рис. 92). В сечении получится четырехугольник, но для решения задачи достаточно рассмотреть отношение объемов пирамид PMLK и QMLK с общим основанием

MLK .

Если SABD a, то

где VABCD V .

Аналогично получаем VQKLM 11V (до60

кажите!). Отношение

PN VPKLM 7V :11V 7 .

QN VQKLM 60 60 11

Решение. Так как ребро AD перпендикулярно плоскости основания, то объем V пирамиды DABC равен

Так как медиана BT делит площадь треугольника ABC пополам, то объем

пирамиды DATB будет равен V 28. 2

MC1 :MC n. Тогда объемы пирамид MA1B1C1 и MABC связаны формулой

VMA1B1C1 k m n VMABC . (*)

(См. опорную задачу 12).

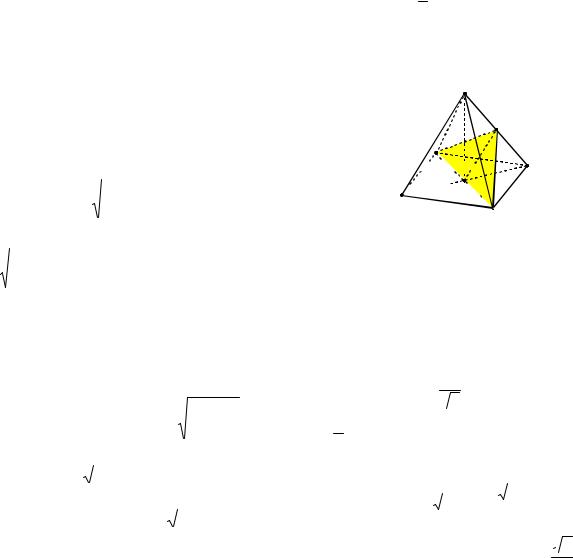
Пример 86. В основании пирамиды DABC лежит треугольник ABC, в ко-

T

A B

Рис. 93

Точки M, N, P лежат на ребрах пирамиды DATB (см. рис. 93), поэтому по формуле (*) получаем

Ответ: 10 . 3

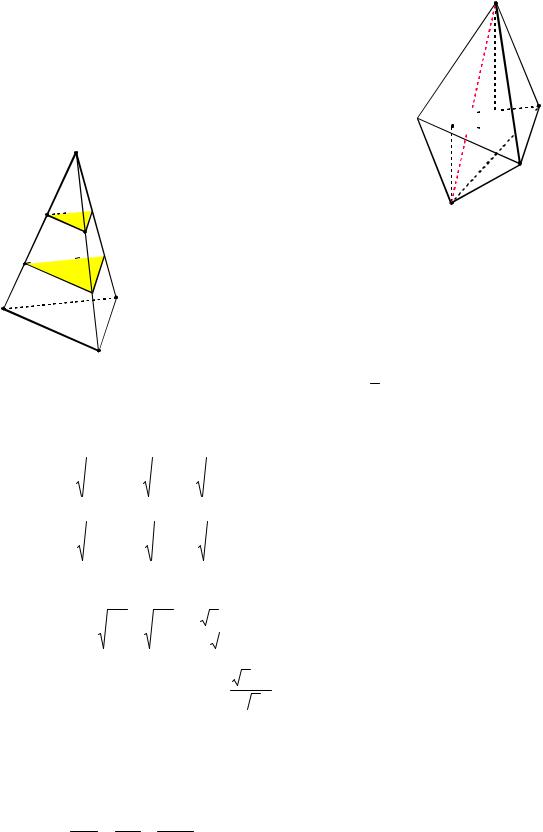
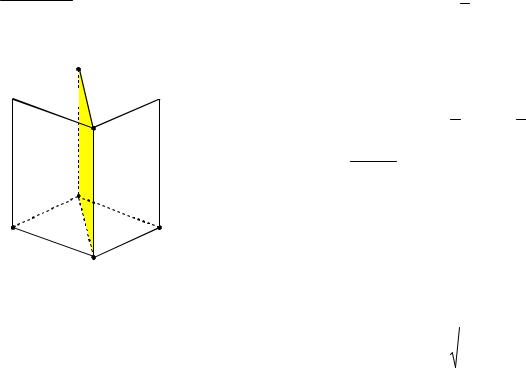
Пример 87. В правильной четырехугольной пирамиде MABCD все ребра равны. Точки P и N – середины ребер BM и DM . В каком отношении делит объем пирамиды сечение, проходящее через прямую AP параллельно диагонали основания BD?

Решение. Так как точки P и N – середины ребер BM и DM, то PN – средняя линия треугольника BMD и PN || BD. Так как через точку P можно провести единственную прямую, параллельную BD и секущая плоскость также параллельна BD, то PN лежит в плоскости сечения (см. рис. 94а).

Так как пирамида правильная, то MO

– высота пирамиды (O – точка пересече-

ния диагоналей основания),

MO BMD CMA.

Пусть точка E PN MO, тогда E – середина MO. Тогда прямая AE также

что MK :MC 1:3.

Плоскость CMA разбивает каждую из пирамид MABCD и MAPKN на две равные треугольные пирамиды. Используя соотношение (*), получаем

1

Аналогично, VMKNA 6 VMCDA .

Соответственно, объем пирамиды MAPKN будет составлять шестую часть объема данной пирамиды, а секущая плоскость будет делить объем в отношении 1:5.

Ответ: 1:5. ● Пусть a и b – длины двух противопо-

V1 abdsin . 6

(См. опорную задачу 9).

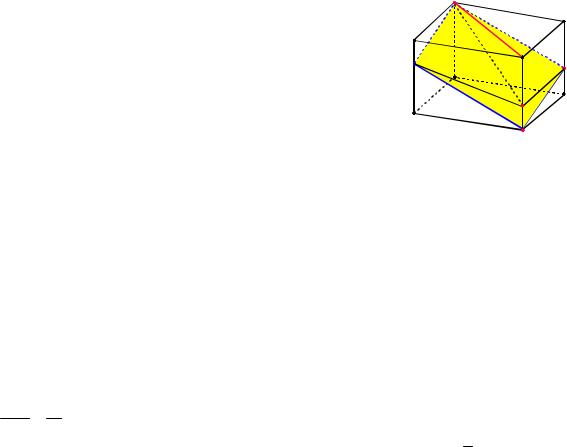
Пример 88. Дан единичный куб АВСDA1B1C1D1 . Найти объем пирамиды АB1CD1.

Решение. Имеем АB1 CD1 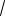2 (см.

рис. 95). Расстояние между скрещивающимися прямыми АB1 и CD1 , лежащими в параллельных плоскостях, равно 1. Угол между ними равен 90 , так как АB1 ||DC1 и CD1 DC1 . Следовательно,

B

AC

D

Рис. 95

1

VAB1CD1 6 AB1 CD1 AD sin (AB1;CD1)

1 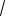2 2 1 1 1 . 6 3

Ответ: 1 . 3

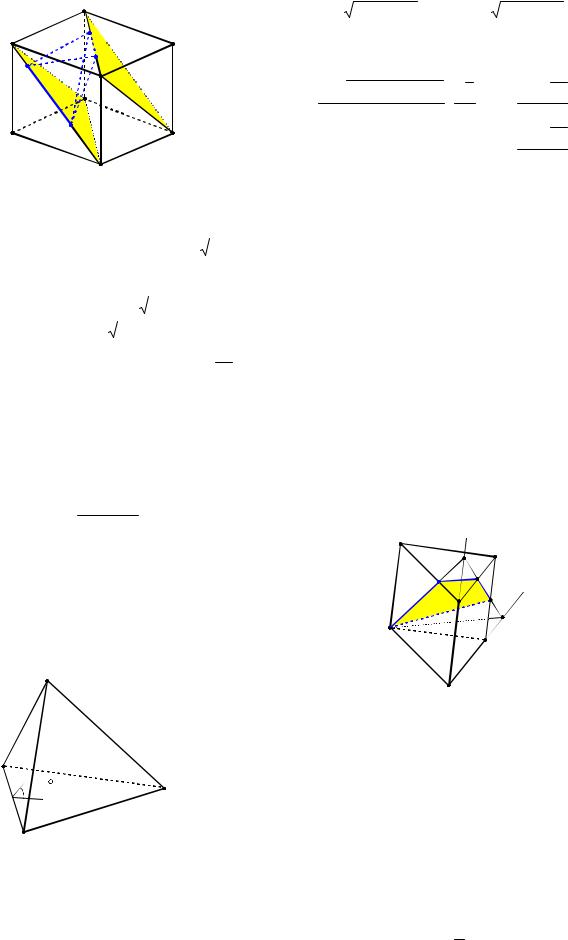
Пример 89. На диагонали грани единичного куба взяты точки М и N, а на скрещивающейся с ней диагонали соседней грани взяты точки P и Q. Известно,

АВСDA1B1C1D1 (см. рис. 96). Отрезки MN

и PQ лежат на прямых AB1 и A1C1 соот-

Ответ: 1 . 72

● Пусть p и q – площади двух граней тетраэдра, a – длина общего ребра, – величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле

V 2pqsin .

3a

(См. опорную задачу 11).

Пример 90. Найдите объем пирамиды

8

A

Рис. 97

Решение. Используя формулу Герона, находим площади треугольников (см.

рис. 97) ABD и ABC:

18.02.2011

Тогда искомый объем пирамиды равен

V 2 172 92 3 5 7 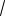3 :12 153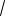35 . 16 2 64

Ответ: 15335 . 64

принцип разбиения и дополнения

Иногда при вычислении объема многогранника используют дополнение этого многогранника до пирамиды (призмы) или разбиение на эти фигуры.

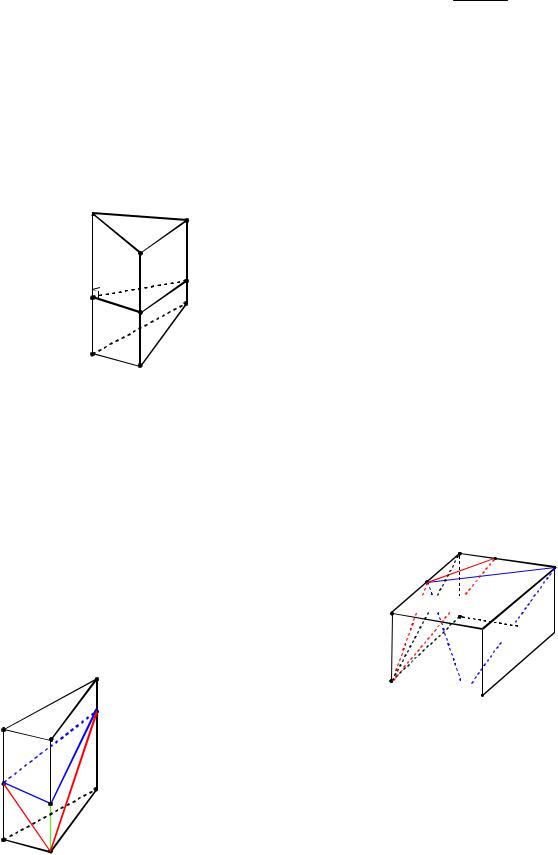
Пример 91. В треугольной призме АВСA1B1C1 с объемом 180 см3 проведено сечение через вершину A и середины ребер BB1 и B1C1 . Найти объем отсеченной части призмы, содержащей ребро

CC1 .

Решение. Обозначим через М и N середины ребер BB1 и B1C1 соответственно (см. рис. 98). Далее находим точки

S MN CC1 и P SA A1C1 , и в сече-

нии получим четырехугольник APNM .

C

Рис. 98

Построим точку L MN BC . Пусть Н – высота призмы, Q – площадь основания. Объемы пирамид SALC , SPNC1 и

MALB обозначим через V2 , V3 , V4 .

Точки М и N – середины ребер, поэтому

пирамиды SALC равна 3 H . 2

55

Объем

Объем отсеченной части призмы, содержащей ребро CC1 равен

V2 V3 V4 135 5 15 115 (см3).

Ответ: 115 см3.

Пример 92. (ЕГЭ 2008). Дан прямо-

угольный параллелепипед ABCDA1B1C1D1.

На его боковых ребрах AA1 и BB1 лежат точки M и P соответственно так, что

AM :MA1 8:11, B1P: PB 2:1. Во сколько раз объем данного параллелепипеда больше объема пирамиды с вершиной в точке P , основанием которой является сечение данного параллелепипеда плоскостью BMD1?

Решение. Объем V данного параллелепипеда равен V CB BA BB1 (см. рис. 99). Сечение параллелепипеда плоскостью BMD1 – параллелограмм BND1M , который делит его объем пополам и

C1N 8 (см. опорную задачу 21).

NC 11

две пирамиды D1NC1B1P и D1PB1A1M и найдем объем каждой из них, учитывая, что противоположные ребра параллелепипеда равны.

Ответ: 9.

Треугольную пирамиду можно достроить до параллелепипеда двумя способами.

1-й способ. Треугольник АВС достраиваем до параллелограмма АВЕС, затем до параллелепипеда ABECA1B1E1C1 (см. рис. 100). В этом случае

1

VABCA1 6VABECA1B1E1C1 .

(См. опорную задачу 7).

E1

B1

C1

A1

E

B

C

A

Рис. 100

Пример 93. В треугольной пирамиде боковые ребра взаимно перпендикулярны

и имеют длины 70 , 99 и 126 . Найти объем пирамиды.

Решение. Данную пирамиду достраиваем до прямоугольного параллелепипеда. Тогда искомый объем равен

V1 70 99 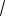126 21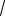55 . 6

Ответ: 2155 .

2-й способ. Проводим через каждое ребро тетраэдра плоскость, параллельную противоположному ребру (см. рис. 101). В этом случае ребра исходного тетраэдра являются диагоналями граней получившегося параллелепипеда и

1

VABCD 3VDECFHAGB .

B

H

G

A

F

D

C

E

Рис. 101

Пример 94. Два противоположных ребра треугольной пирамиды равны а, два других равны b, два оставшихся – с. Найдите объем пирамиды.

Решение. Достраиваем данный тетраэдр до параллелепипеда, проводя через каждое ребро плоскость, параллельную противоположному ребру. Согласно условию задачи получаем прямоугольный параллелепипед (диагонали в каждой грани равны). Пусть линейные размеры параллелепипеда соответственно равны AB x, AD y , AA1 z (сделайте рисунок). Исходя из условия, составим систему уравнений

● Объем треугольного призматического

где плоскость АВС перпендикулярна ребрам призматической поверхности (см.

рис. 102).

A2 C2

(См. опорную задачу 13).

Пример 95. Площадь основания АВС прямой треугольной призмы ABCA1B1C1 равна 30. Точки F, E, D лежат на ребрах AA1 , BB1 , CC1 соответственно, причем AF 4. Найти объем треугольной пирамиды DAFE.

объем

VDAFE 4 0 0 30 40.